なぜ内積は成分同士の積になるか
ベクトルの内積 |A||B|cosθは、各成分ごとの積を足し合わせた値に等しくなる。
確かに計算するとそうなるのですが、なぜそうなるのか、直観的には把握しずらい。
そこで、内積を直観的に見てとれるように、片方のベクトルを90度回転して図示してみます。
最も簡単な、2つのベクトルが同じ向きにそろっていた場合の図は、こうなります。
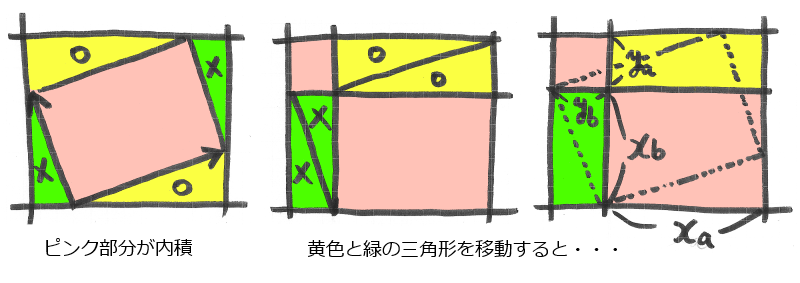
こうすれば、内積の値を「長方形の面積」として見ることができるでしょう。
この長方形を直交座標の上に置いて、下図のように、周囲の三角形を移動すれば・・・
確かにピンク色の部分が、各成分ごとの積和 Xa・Xb + Ya・Yb に一致しますね!
では、2つのベクトルの向きがそろっていない場合はどうなるか。
この場合は、上で長方形について行ったことを、平行四辺形に拡張しただけなのです。
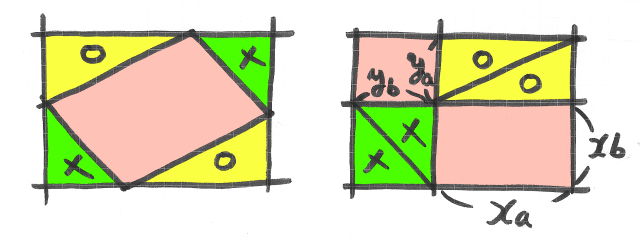
先ほどと同様、片方のベクトルを90度回転して図示します。
そして、平行四辺形の周囲にある三角形を移動すると・・・
確かに、ピンク色の部分 = |A||B|cosθ = Xa・Xb + Ya・Yb となっているではありませんか!
※ 実はこの内積の証明、実質的にピタゴラスの定理と同じことなのです。
※ ・ピタゴラスの定理と内積の関係 >> d:id:rikunora:20180503
※ ちなみに、高校の教科書には「余弦定理による証明」というものが書かれていた。
※ むろん、正当な方法なのだが(私にとっては)いまひとつ直観的ではなかった。
※ 参考: http://izumi-math.jp/G_Kakuta/in_pro/in_pro.htm
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- -
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
* 物理講座のお知らせ
来る 6/16(日) に、物理学講座6月分を行います。
主催は「みけねこサイエンスプロジェクト」の「かっぱはかせ」。
>> http://geocities.yahoo.co.jp/gl/mikeneko_science/view/20130604
13:30-15:00 「微分から始める、惑星軌道を計算しようコース」 第6回:運動量ってなぁに?
15:30-17:00 「量子力学講座」 第5回:あいまいでデジタルな量子力学(過去回の復習を含みます。)
* 参加費: 3,000円
* 会場: (株)モーション 会議室
毎月1回のペースで続いています。
ご興味ある方は、ぜひどうぞ。内積の話題も、ここから来ています。