円を開く

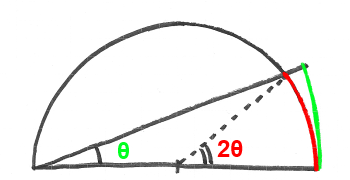
まずはこの図を見て下さい。

図において、赤い円弧と緑の円弧の長さは同じです。
なぜかというと、半径を２倍にした代わりに、中心角を半分にしたから。
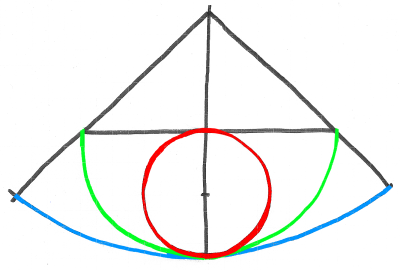
上の図の意味が分かったところで、今度は下の図を見て下さい。

今度の図では、赤、緑、青の円弧は全て同じ長さです。
理屈は上と同じで、半径を倍、倍、にした代わりに、中心角を半分ずつにしています。
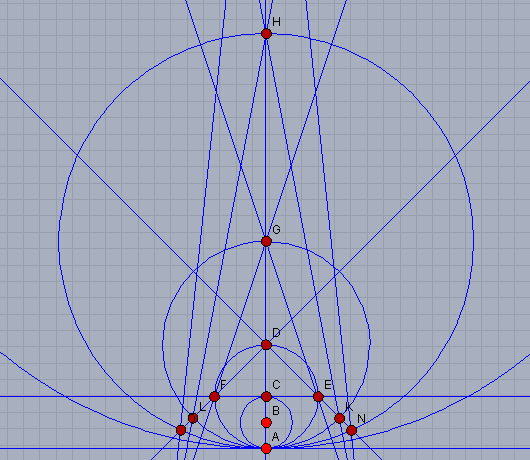
同じ操作をもっと繰り返したのが次の図です。

ここでは操作を５段階まで繰り返しました。
※ こういった幾何学図形を描くのに便利なソフトが Cinderella（シンデレラ）です。
※ 上のような図がおもしろい様に描けるので、ぜひお試しあれ。
※ 参考: >> 271828の滑り台Log -- いとしのCinderella

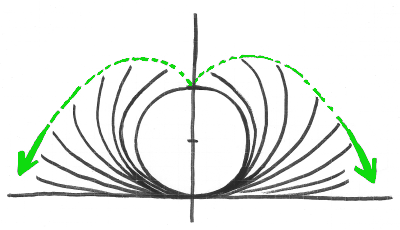
以上の操作を繰り返すと、円周を長さを変えずに切り開いていく過程が見えてきます。

こんな感じ。
ここで気になるのは、切り開いていったときの軌跡、緑の矢印で示した曲線でしょう。
この曲線はどういった形なのかというと、
「円の半径を伸ばした分だけ、中心角を小さくする」という規則に従って描かれています。
式にすれば、{ r Sin(1/r), ± r (1 - Cos(1/r) } という点の集まりです。（r は円の半径）
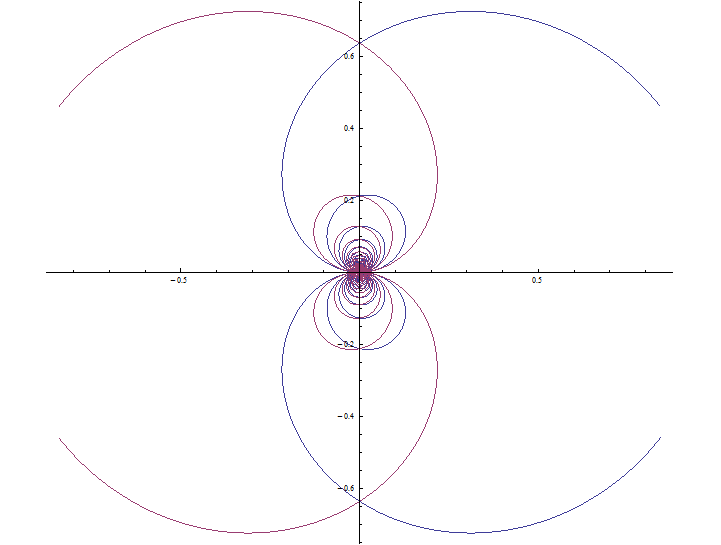
この点の集まりをプロットすると・・・

こうなりました。
原点の近くで、クルクルっと小さな渦巻きを形作っています。
これ、どういうことかというと、切り開く動作(r > 1)と反対の、
小さく丸めていった方(-1 < r < 1)もプロットされているのです。
一定長の円周を小さく丸めてゆくと、やがて円周は１巻き、２巻き、３巻き・・・
と巻き数を増していって、１点にまで縮めた極限では無限回巻き?! になります。
さらに、その極限を通り越して反対側 (r < 0, rがマイナス) に突き抜けると、
今度は小さな渦巻きが再び開いて元の円に戻る、そんな動きをします。
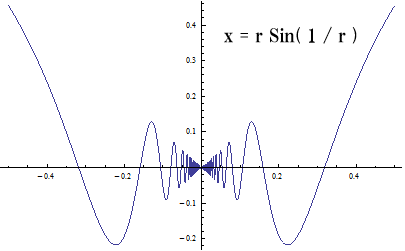
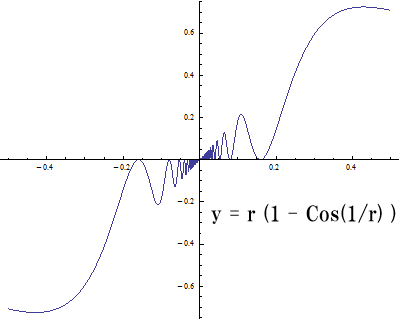
感覚を掴むため、プロットのｘ座標、ｙ座標をそれぞれグラフにしてみました。

y = x Sin( 1 / x ) という関数は、しばし０点で連続なのだろうか？ という例題に取り上げられます。
厳密に言えばε-δのような議論が必要なのでしょうが、
直観的には、小さく丸まった円を想像すれば、実は連続なのだということが納得できると思います。

※ だからどうした！ って言われると、オチは無いのですが、、、
※ 単に丸まった形がおもしろい、というだけです。以上。