ラグランジュ方程式のイメージ解釈
ラグランジュ方程式とは、解析力学を初めとする物理学の基礎を成す方程式です。
∂L( q(t), q'(t), t )/∂q(t) - d/dt{∂L( q(t), q'(t), t ) /∂q'(t) } = 0
-- wikipedia:オイラー=ラグランジュ方程式
ちょうど関数の最小値を求めたいとき「微分=0」を調べるのと同じように、
汎関数(関数の関数)の最小値を求めたいとき、このラグランジュ方程式を調べます。
ただ、「微分=0」には“谷底の傾きは平らになる”という明確なイメージが描けるのに比べて、
ラグランジュ方程式のイメージを思い描くのはかなり難しい。
数学が相当得意な人であっても、記号の字面を追うのが精一杯、というのが実情でしょう。
ラグランジュの『解析力学』という本には、イメージを助ける図が一切ありません。
「緒言」でラグランジュ自身が述べているように,この本には「図がまったく見出され」ず,必要とされるのは「代数的な操作のみ」である.
-- <翻訳> J・L・ラグランジュ『解析力学』(抄)
-- https://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/137415/1/phs_5_127.pdf
そもそも解析力学とは、
「代数的な操作こそが正当であり、幾何学的な図は本来排除されるべき補助手段に過ぎない」
という思想の産物だったのです。
この思想は現代でもなお有効で、高度抽象的な対象を前にして、私たちは
イメージ化をスッパリ諦めるか、
邪道であっても図を思い描くか、
の2択を迫られているわけです。
ラグランジュ方程式が難しいと感じる本当の理由もここにあって、
最初からイメージ化を諦めてかかった方がむしろ受け容れやすい、という側面があります。
にもかかわらず、ここではあえて邪道なイメージ化の方法を試みます。
ラグランジュさんには申し訳ないのですが、私たち凡人はイメージ化して初めて腑に落ちたと感じるからです。
ラグランジュ方程式の骨格を読み解くため、いったん“微分”という要素を棚上げし、
まず“関数の関数”という要素だけに着目しましょう。
いま、
L(t) = t^2 - 2 t
という、t の関数があったとしましょう。
ここで L の最小値を求めよと問われれば、関数 L(t) を t で微分するのが常套手段なのですが、
ここではあえて次のような見方をとります。
T(t) = t^2
U(t) = 2 t
と置いて、
L( T(t), U(t) ) = T(t) - U(t)
という“T と U の関数L”を作ります。
このとき L の最小値を求めるには、
T と U がちょうどバランスをとって等しくなる点、T' = U' を探せばよい、
ということになるでしょう。
T'(t) = 2 t
L'(t) = 2
2 t = 2 を解いて、t = 1 のとき L は最小となる。

こんな手間をかけて何が嬉しいのかというと、最小値についてのイメージが変わります。
関数 L(t) を直接 t で微分するとき、最小値とは“傾きが0となる点を探す”ということでした。
一方、L(T,U) = T - U を間接的に t で微分したとき、最小値とは“T' と U'がバランスをとって打ち消し合ったとき”という意味に変わります。
“傾きが0となる点”という見方をするなら、最小値は“点”として得られました。
一方、“バランスをとって打ち消し合う”という見方をするなら、
T'=U' を満たす点を列挙することで、最小値を“線”として得る道が拓けます。

ここに変分法 ~ 最小となる関数を求める方法 ~ のカラクリがあります。
解析力学における「ダランベールの原理」も、結局はこの“バランスをとって打ち消し合う”ことを意味しています。
運動する物体は、局所局所において、静的な力と、動的な加速(に由来する力)が打ち消し合っている。
なので、そうしたバランスを保つ点を線で結べば、運動の軌跡が自ずと浮かび上がるだろう。
これが、ラグランジュ方程式を形作るアイデアだったのです。
“バランスをとって打ち消し合う”ことを経済に例えるなら、需要と供給の均衡点のようなものです。
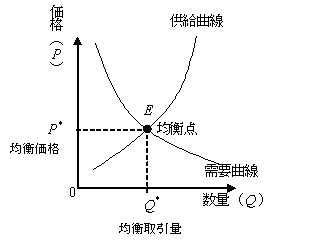
-- wikipedia:需要と供給 より引用
ラグランジアンとは、余計なエネルギーコストという意味で、経済で言うところのコストと高い親和性があります。
仮に「需給のバランスがとれた姿が実現すべき社会である」と考えるなら、
需給バランスを原理原則として、社会の姿を予言(計算)できることになるでしょう。
たとえば原料価格を横軸にとって、均衡点を線で結べば、原料価格に対する適正な生産量のグラフが描けます。
あるいはもし、消費者の満足度のようなものが数値化できれば、
満足度を横軸にとって均衡点を線で結べば、適正価格のグラフが作れるはずです。
※ 私は経済学には疎いのですが、どうも昨今の経済学(の一派)は、そういう事をやっているみたいです。
※ 『大学二回生のときに「解析力学」の講義で習ったラグランジュの方程式が、なぜかミクロ経済学の教科書にそのまま書かれているのである。』
※ * 現実と違っても数学モデルを信仰してしまう経済学者たち >> http://data11.web.fc2.com/jiyuuboueki5.html
需給バランスの例で言うと、オリジナルのグラフは横軸が「数量」となっています。
この1枚のグラフから得られる答は「均衡点」というただ1点のみであり、
それだけで終わっていたなら、需給バランスのアイデアはここまでありがたがられなかったことでしょう。
需給バランスが有用なのは、オリジナルのグラフの上にさらにもう1次元、原料価格とか、満足度とかいった、新たな変数が追加できるところにあります。
オリジナルの均衡“点”は、新たな変数 ~ 原料価格に対する“線”、あるいは満足度に対する“線”となります。
さて、だいぶ持って回した言い方となりましたが、先ほどの単純な例、
L(T,U) = T(t) - U(t) = t^2 - 2 t
に立ち返ると、そこにあったのは変数 t のみで、このままで終わっていては何のありがたみも感じられません。
変数 t の上に、新たな変数、位置 q と、速度 q' をオーバーラップさせて初めて、
・位置 q に対する均衡の線
・速度 q' に対する均衡の線
が描けるわけで、ラグランジュ方程式の真価が発揮されるのです。
※ 解析力学では、物体の位置を x と書かずに q と書くことが多いです。
※ x がいわゆる直交座標を表すのに対し、q は広く一般的な座標という気持ちが込められています。
改めて、先ほど省いてきた“微分”の要素に目を向けましょう。
ラグランジアンLを、本来の姿、
L( q(t), q'(t) )
に戻します。
つまりラグランジアン L とは、位置 q と、速度 q' の関数です。
※ 本来であれば、さらに時刻 t も含めるべきなのですが、簡単のため省略します。
冒頭に掲げたラグランジュ方程式の骨格のみを抜き出すと、こうなります。
∂L/∂q = d/dt{ ∂L/∂q' }
ラグランジアン L を「エネルギーコスト」と読み替えると、この式は、
「エネルギーコスト L に対する、位置 q の寄与と、速度 q' の寄与が均衡している」と読むことができます。
あるいは、「静的な力と動的な力が均衡している」と読むこともできるでしょう。
(そして、位置と速度が均衡しているとき、エネルギーコストは局所的に最小となる、というのがこの式の使い方です。)
ただ、式を見ると、速度 q' のある右辺には d/dt という操作が施されています。
この d/dt を、どう解釈すべきでしょうか。
最も邪道にして簡単な解釈は“約分”です。
速度 q' という記号を、ライプニッツ流の書き方 dq/dt に直してみましょう。
(どちらの書き方でも、t で微分する、という意味は同じです。)
そして、d/dt という記号は“約分”できる、とするなら、
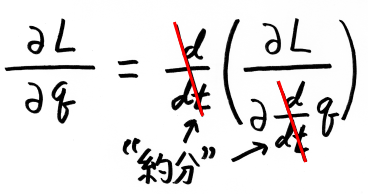
このように、ラグランジュ方程式とは(少なくとも強引な字面の上では)極めてアタリマエのことを主張していたのです。
“約分”よりもう少しまっとうな解釈は、「単位時間当たり」という操作の必然性です。
d/dt には「単位時間当たり」という意味があります。
仮に、時間がゆっくり流れているスローモーションの世界があったとしましょう。
スローモーションの世界では、時間はゆっくりになりますが、運動の軌跡は同じ形のままです。
時間がゆっくりになっても、位置 q の寄与(位置 q に依存する静的な力)は変わりません。
一方、時間がゆっくりになったとしたら、速度 q' の寄与(速度 q' に依存する動的な力)は小さくなるはずです。
それでも軌跡が同じだということは、速度 q' の寄与を、時間の流れる速さに合わせて調整しなければなりません。
どのように調整するかというと、時間の流れる速さで割ってやる、つまり「単位時間当たり」の量に換算します。
これが速度 q' の寄与 {∂L/∂q'} に d/dt という操作を施す理由です。
もし時間がゆっくり流れる世界が認められないのなら、時間の単位を変えて計算することを考えてみてください。
運動の軌跡は、秒単位で計算しようとも、分単位で計算しようとも一致するはずです。
にもかかわらず、単に {∂L/∂q'} を計算すると、秒速の方が分速の 60倍となり、静的な力 ∂L/∂q と釣り合いがとれなくなってしまいます。
(静的な力の方には、陽に単位時間が入っていないことに注意。)
方程式が成立するためには(つまり方程式の両辺の単位を合わせるには)、{∂L/∂q'} を時間の単位で割る必要があります。
※ この時間単位を揃える操作 d/dt と、そもそも速度とは位置の時間変化であった dq/dt とは、表記の上では“約分”のように打ち消し合います。
以上のお膳立てが整ったところで、ラグランジュ方程式のイメージ化を試みましょう。

まず横軸に時刻t、縦軸に物体の位置qをとり、運動の軌跡を描きます。
これに高さの軸Lを追記し、3次元のグラフを形作ります。
Lは物体の位置qに依存するので、それをq×L平面上に描きます。
q×L平面上に描かれた軌跡の傾きは、∂L/∂q を意味します。
ここまでは静的な力の話で、図の上では青色で描かれています。
次に、運動の軌跡を微分した速度q’の線をt×q平面上に重ねて描きます。
速度q’の軸は、位置qの軸とスケール(単位目盛り)が異なっているため、改めて図の右側にq’軸を付け加えました。
つまり微分したq’の線は、右側のq’軸の方を用いたt×q’平面上にあるものと考えます。
(図の上で、t×q平面とt×q’平面は重ねて描かれています。)
Lは物体の速度q’にも依存するので、それを描く平面が必要です。
図の上に、速度q’軸に直行する形で、高さ軸 d/dt(L) を付け加えましょう。
(図の上で、右端で垂直に立っている平面がq’×dt/d(L)平面となります。)
この q’×dt/d(L)平面上に描かれた軌跡の傾きは、d/dt(∂L/∂q') を意味します。
ここまでが動的な力の話で、図の上では赤色で描かれています。
こうして描いた3次元のグラフを、横方向から眺めてみましょう。
横軸にqとq’のオーバーラップ、縦軸にLとdt/d(L)がオーバーラップした、
2枚の青と赤の重なったグラフが見えることになります。
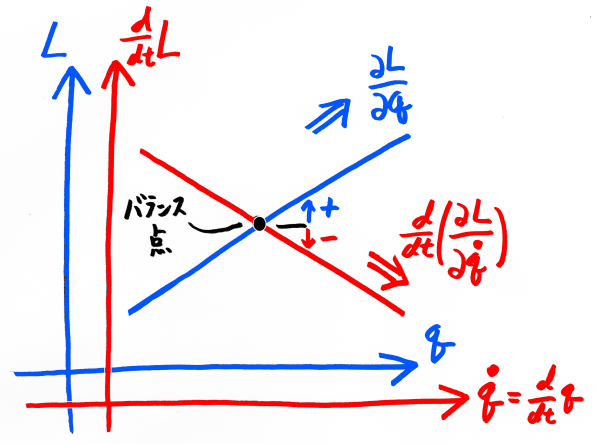
青いグラフの上には、Lに対する位置 q の寄与(位置 q に依存する静的な力)が描かれています。
赤いグラフの上には、Lに対する速度 q' の寄与(速度 q' に依存する動的な力)が描かれています。
このとき、Lを局所的に最小とするのは、2つの力の均衡点となります。
逆に、この均衡点を計算しながら辿っていくことで、もとの運動の軌跡が再現できます。
そして、均衡点を表す式とは(静的な力)=(動的な力)という形をとり、記号で書けば
∂L/∂q = d/dt{ ∂L/∂q' }
これがラグランジュ方程式です。
* まとめ *
・微分というツールを、“傾き=0”ではなく、“2つの勢力がバランスをとって打ち消し合った均衡”であると捉える。
・ラグランジアンLを、「エネルギーコスト」と読み替える。
・2つの勢力を、
(1) エネルギーコストLに対する位置 q の寄与(位置 q に依存する静的な力)
(2) エネルギーコストLに対する速度 q' の寄与(速度 q' に依存する動的な力)
に対応させる。
・(1) と (2) は同じ土俵(座標系)の上には乗らない。
なぜなら、静的な力が単位時間を含まないのに対し、動的な力は単位時間を含むからである。
そこで、動的な力の方に d/dt という操作を加え、同じ土俵に乗せる。
・こうしてできた均衡の式が、ラグランジュ方程式だ。
∂L/∂q = d/dt{ ∂L/∂q' }
最後に、以上のようなイメージ解釈は冒頭にも述べた通り、ラグランジュさんの精神からすれば邪道なのであって、
いわゆる教科書流の「代数的な操作のみ」による証明が正道であるとされています。
しかしなぜ、代数的操作は正しく、イメージ解釈は受け入れがたいのでしょうか。
天才ラグランジュさんとて人の子であり、おそらく誰よりも明確なイメージを抱いていたはずです。
そのイメージを公開しなかった理由の1つは、逆説的ですが、
『イメージは正しく人に伝わらないから』
ではないかと思うのです。
凡才である私がラグランジアンの図を描きつつ浮かんだのは、
「この図の意図は、なかなか人には伝わらないだろうな・・・」
という思いでした。
図の読み手が悪いという意味ではなく、この図では意図が描き切れていない、表現力が足りないという意味です。
もう少し具体的に言うと、“時間の流れを揃える”といった感覚を図にすることができません。
もちろん、自然言語で表すことも難しい。
インターラクティブなアニメーション、dtをビヨーンと引き延ばすと、それに伴って {∂L/∂q'} が変化するようなオブジェクトを作れば、もう少し表現できるかもしれません。
それでも完全ではありません。
勝手な想像ですが、天才ラグランジュさんは、自分の持つイメージが当時の人たちにはまず伝わらないと悟ったのではないでしょうか。
その上で、驚くべき方法 ~ 代数的操作のみによって表現する方法を開拓したのだと思うのです。
それがあまりにもすごかったものだから、後世の人がすっかり「代数的な操作のみが真実」であると信じ込んでしまった。
確かに、代数的な記号操作はイメージよりも誤解が少ないし、コピーするのも難しくはありません。
しかし、ただコピーしただけでラグランジュさんの意図が伝わったのかというと、そこには依然、大きなギャップがあるものと思うのです。
代数的操作による説明は、以下を参照。
* ラグランジアンに意味は無い >> d:id:rikunora:20090327