30年目の書籍化 ~ 現代経済学の直観的方法

『私は30年前にこの本のベースとなる論考に出会い大きな衝撃を受けた。』
そして、後書きの一文に着目。
『足かけ20年の形で本書の書籍化に関わっていただいた・・・・』
つまり、この本のベースは何と30年前から存在していたのです。
30年前から密かに出回っていた、言ってしまえばごく内輪向けのテキストが、
廃れることなく少しずつ加筆・修正を繰り返し、ついに公に書籍化されたというのがこの本なのです。
・・・ちょっと異例の経緯だと思います。
考えてみてください。この30年間、経済の世界でどれほどの激動があったことか。
その間、多少の修正はあれど、芯が全くブレていない。正直、それだけでも驚きです。
私がこの内輪向けのテキストを最初に読んだのは2001年ごろ、19年前になります。
そして、“布教活動”を開始したのが10年前です。
rikunora.hatenablog.com
今回の書籍化にあたり、古い電子版の方は販売を中止します。
古い版になりますが、冒頭部分だけは試し読みができます。
* 旧:電子版 -- 第1章の試し読み
>> http://book.motion.ne.jp/pathfind/Economy_Sample.pdf
で、内輪の人が何を言ってもバイアスがかかるので、ただ
「すごく昔からあって、異例の経緯を経て世に出た」
という事実のみを伝えておきます。

- 作者:長沼 伸一郎
- 発売日: 2020/04/09
- メディア: 単行本(ソフトカバー)
※ 本書と似たカラーを持つ“(30年と比べて)ここ最近のベストセラー”に、こんな本があります。

シン・ニホン AI×データ時代における日本の再生と人材育成 (NewsPicksパブリッシング)
- 作者:安宅和人
- 発売日: 2020/02/20
- メディア: 単行本

父が娘に語る 美しく、深く、壮大で、とんでもなくわかりやすい経済の話。
- 作者:ヤニス・バルファキス
- 発売日: 2019/03/07
- メディア: Kindle版
※ 実はこの「現代経済学の直観的方法」、決して万人に受ける内容では無いだろうと(私は)思っています。
※ ただ、上の2冊に関心のある人ならば、間違いなく琴線に触れることを請け合います。
コロナ感染者数データに指数曲線あてはめ
タイトルの通り。元データは以下から取得、これは東京都の場合。
* 東京都オープンデータカタログサイト >> 東京都 新型コロナウイルス陽性患者発表詳細
>> https://catalog.data.metro.tokyo.lg.jp/dataset/t000010d0000000068
あてはめた結果が、これ。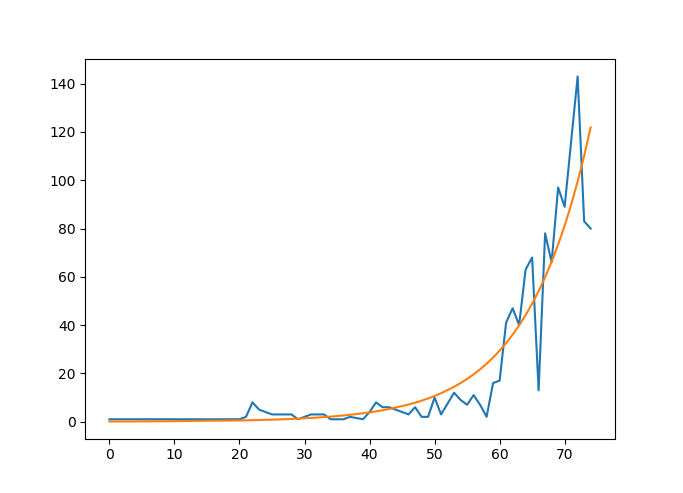
そのまま180日、約半年に期間延長してみる。
★もちろんこれは簡易的なあてはめなので、もっと信頼のおける予測は「SIRモデル」などのキーワードでググってください。
* COVID-19情報共有 >> https://www.fttsus.jp/covinfo/
import numpy as np import pandas as pd import matplotlib.pyplot as plt from scipy.optimize import curve_fit DATA_FILE = "130001_tokyo_covid19_patients.csv" # 読み込むCSVファイル df = pd.read_csv( DATA_FILE ) df = df.rename( columns={"公表_年月日" : "day"} ) # 日本語名をリネームしておこう df['day'] = pd.to_datetime(df.day) # 日付型に変換 df['count'] = 1 # 1行1件とカウントする df = df[ ['day', 'count'] ] # カウント以外は削除 grouped = df.groupby("day").sum() # 日付で集計 x = np.array( grouped.index.map(pd.Timestamp.timestamp) ) # 日付->秒数に変換 base = x[0] # スタートを0日とする day_unit = (24*60*60) # 1日単位に変換する x -= base x /= day_unit y = np.array( grouped['count'] ) # フィットしたい関数 def func( x, a, b ): return np.exp(a * x + b) # 指数関数をあてはめてみよう params, _ = curve_fit( func, x, y ) plt.plot(x, y) plt.plot(x, func(x, *params)) plt.show()
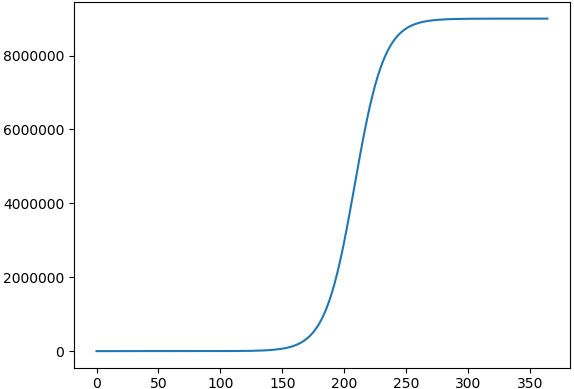
■ 2020/04/15 追記、指数ではなく、ロジスティック曲線をあてはめるには、以下のように差し替える。
# フィットしたい関数 def func( x, a, b ): max_pop = 9000000 # 東京都の最大人口を9百万人とする return ( max_pop / (1 + np.exp( -(a * x + b) ) ) )
<< 超訳・物理学 >>
“ラグランジアン”と“エントロピー”、この2つを受け入れれば、古典物理学は理解できる。
さらに“光速度”と“プランク定数”、この2つを受け入れれば、現代物理学は理解できる。
=== 古典力学 ===
【相対性原理】
あらゆる慣性系(観測者の立場)は同等であり、特別な慣性系は存在しない。
【最小作用の原理】(停留作用の原理)
物体の運動にともなって変化する“ラグランジアン”と呼ばれる量がある。
あらゆる物体の運動は、ラグランジアンの合計値(時間についての積分)を最小とする形で実現する。
ラグランジアンの合計値のことを“作用”という。
外力の影響を受けない物体の運動に、何らかの最小作用を満たすような値があるとすれば、
その値は相対性原理から、速度の2乗の関数でなければならない。
その速度の2乗の関数を、我々は“運動エネルギー”と呼んでいる。
さらに、物体がその位置から受ける影響(外力の影響)を“位置エネルギー”と呼び、
{(運動エネルギー)-(位置エネルギー)} を“ラグランジアン”と定義する。
あらゆる物体の運動は、
S = ∫ L dt
-- S:作用, L:ラグランジアン, t:時刻
が停留値をとる形で実現する。
=== 熱・統計力学 ===
=== 一般相対性理論 ===
=== 場の理論 ===
重力を空間の幾何学的な歪みとして理解できるように、あらゆる種類の力、例えば電磁気力などもまた、ある種の空間の幾何学的な歪みとして理解することができる。
※ ある種の空間のことを“場(Field)”という。
あらゆる場は、ローレンツ不変である(光速度不変の原理を満たす)。
それぞれの場には、対応する“ラグランジアン”がある。
それぞれの場における運動もやはり、対応するラグランジアンの作用が最小となる形で実現している。
=== 量子力学 ===
あらゆる物体は、2乗すると(複素共役と掛け合わせると)存在確率となるような、複素数の波動から成り立っている。
波動とは、振幅と位相を持つ何らかの複素数の量の変動なのだが、その全容を我々が直接観測することはできない。
我々が直接観測できるのは、波動の実数成分だけである。
【不確定性原理】
作用には、それ以上分割できない最小単位がある。
最小単位より小さな値は、どうがんばっても定めることができず、不定な量が残る。
※ この最小単位を“プランク定数”という。
最小単位のため、作用が与えられた場は、離散的にカウントできる(1個, 2個, 3個・・・と区別して数えることができる)状態をとる。
そのカウントできる状態のことを、我々は“粒子”と呼んでいる。
あらゆる物体は、複素数の波であると同時に粒子でもある(状態がカウントできる波である)。
対象がカウントできる状態にあることを ~ つまり“粒子”だと見なせることを、“量子化されている”という。
あらゆる場は、量子化されている ~ つまり“粒子”だと見なせる。
=== 無限・計算理論 ===
無限には大小のレベルがあり、そのレベルのことを“濃度”という。
最も濃度の小さな無限は、1,2,3・・・と続く自然数の無限で、“可算無限”と呼ばれている。
数直線上の点の数は、“可算無限”より濃度の大きい“非可算無限”である。
濃度は、それもまた無限に大きくなり得る。
数直線上の点の数よりさらに濃度の大きい無限が、無限に存在する。
計算機械の持ち得るアルゴリズムの全ては可算無限なので、本質的に非可算無限に属する問題を解くことはできない。
どんなアルゴリズムを以てしても、この世のほとんどの問題は解けない。
言いたかったのは以上なので、以下は蛇足。
きっかけは以下のひと言にあった。
「力学はラグランジアンという1個の量だけ認めれば定式化でき、熱力学はエントロピーという1個の量だけ認めれば定式化できる」
>> http://as2.c.u-tokyo.ac.jp/~shmz/zakkifiles/07-08-21.html
実際、「熱力学の基礎」という本では、エントロピーから他の全てを導いている。
温度という当たり前に思える量でさえも、エントロピーから導かれる。
「ランダウ力学」という有名な(しかし高度な)教科書では、ラグランジアンから他の全てを導いている。
物理学とは恐ろしいほどまでに体系立った学問で、ほんのわずかの基礎原理から、他の全てが導出される。
“暗記”は極限まで少なくて、あとは“考えれば分かる”のだ。
では、物理学に最低限必要な“暗記”はどれだけあるのか?
そう思って必要最低限の“暗記”部分を私なりにリストアップしたのが、上の<< 超訳・物理学 >>となった。
最低限、これだけ頭にたたき込んでおけば、あとは“考えれば分かる”はずなのである。
“暗記”が少ない分、うんと考えないといけないのだが、それでも考え続ければ、いつかは必ず分かる。
必ず分かるようにできている。
そのように考えると、最大の謎は
「この世界が、考えれば分かるようにできているのは何故か?」
ということになる。
この謎は <<物理学>> のリストには(今のところ)入らないし、考え続ければ必ず分かる、という保証も無い。
謎である。

- 作者:エリ・ランダウ,イェ・エム・リフシッツ
- メディア: 単行本
なぜ転売ヤーは悪なのか
転売ヤーは経済の仕組みに則って、需要のある所に供給しているだけではないか。
それがなぜ悪いのか?
こっそり転売を行い、ばれたら謝罪している議員がいたようだが、なぜ謝るのか理解に苦しむ。
むしろ正々堂々と、“機転の利く私はこのような方法で経済活動を行いました”と主張すべきではないか。
・・・という意見を、とある若い人から指摘されて、私は即座に気の利いた返答ができなかった。
一両日考えて、きっとこうだろうと思い至った答を以下に記す。
[1].転売ヤーは、決してそれ自体が“悪”なのではない。
[2].ただ、転売ヤーを“悪”にした方が都合の良い人たちは、「転売ヤー=悪」であると主張する。
そのように主張することもまた、悪ではない。
[3].そして、「転売ヤー=悪」だと考える人たちが多数派であるならば、転売ヤー自身は内心“自分は悪くない”と思っていたとしても、公衆の面前で謝るという選択を採用する。
故に、転売ヤーはコソコソ行動する。この選択もまた、悪ではない。
[4].結局、どこにも“悪”は無く、あるのは合理的選択だけだったのである。
[5].転売ヤーと、「転売ヤー=悪」だと考える人たちの、どちらが主流となり、多数決の上での正義を占めるのか?
その選択は最終的に、転売ヤーを利用するか、拒否するかという、消費者の行動にかかっている。
それが自由資本主義社会の意思決定方法というものである。
話を複雑にするので、不正転売禁止法や、条例で禁止されている場合のことは、ひとまず脇に置いておこう。
ここで問題にしたいのは、仮に法律や条例が許したとしたら、転売という行為それ自体が“悪”なのかどうかである。
[1].転売ヤーは、それ自体が“悪”なのではない。
確かに件の若い人が言うように、需要あるところに、適正な価格で供給するのが経済というものである。
もし、10万円出してもマスクを買いたい!という人が居たなら、10万円で売るのが自由市場だ。
そこに、何ら“悪”は無い。
[2].転売ヤーを“悪”にした方が都合の良い人たちは、「転売ヤー=悪」であると主張する。
ならば自由市場に任せて、皆が一斉に価格を吊り上げれば良いではないか、と思うかもしれないが、現にそうなってはいない。
これはどうしたことか。
ここで、自分が「マスクを売るショップの店長」になったつもりで考えてみよう。
店長は、できることなら価格を吊り上げたい。当然、吊り上げた方が儲かる。
それでも大半のショップは、価格の吊り上げを実際には行わなかった。
なぜだろうか。
もちろん、そんなことをすれば即座に顧客の信用を失うからである。
たとえ今日、マスクが10万円で売れたとしても、マスクの品不足はいずれ解消するだろう。
そのときになって、顧客はきっとこう言うに違いない。
「あのショップは品薄だったとき、私たちの足元を見て、とんでもない価格でマスクを売りつけた。
あのときは仕方なく買ったけど、今後、あのショップで買うことは止めよう。」
こうした顧客の気持ちが容易に想像できるので、ショップの店長としては、次の2択を迫られることになる。
(1): 今日の10万円を採るか。
(2): 明日の顧客を採るか。
もし私がショップの店長であったなら、明日の顧客の方を選ぶ。
ここで、店長が情にあふれる人徳者だったか、計算高い功利主義者であったかは、結果に何ら影響を与えない。
(おそらくショップの雰囲気には影響を与えると思うが、今の議論には関係ない。)
とにかく“明日の顧客”を選んだという、結果だけが重要なのである。
逆に言えば、明日の顧客より、今日の10万円を選んだ人たちが“転売ヤー”なのである。
実際、私はとあるショップの店長が転売を行なわなかった経緯を聞いたことがある。
その店長は、たまたまマスクが手に入ったので、ふと“マスク付き商品”の販売が頭をよぎったのだそうだ。
しかし、実際に“マスク付き商品”の販売は行わなかった。
そんなことをしたら、顧客の信用を失うと考えたからである。
ここで冷静に、あくまでも功利的に考えるなら、今日のショップが価格を吊り上げなかったからといって、明日のショップも依然として消費者の味方である、という保証はどこにも無い。
また、価格を吊り上げなかったからといって、顧客が喜んでショップのファンになる、という保証も無い。
ショップと顧客の間で、何か特別な契約を取り交わしたわけではないのである。
「価格を吊り上げなかった → ショップと顧客の相互利益」という図式には、何1つ確かな根拠が無い。
なので、これを「非合理な選択」だと言う人もいるが、私はそうは思わない。
なぜなら、ショップは実際に顧客が買う・買わないの行動結果を示す“前に”、手持ちの情報だけで判断を下さなければならないからである。
ショップにしてみれば、何らかの確実な根拠に基づいて“本当に”顧客の信用が得られるかが問題なのではない。
顧客の信用を“落とすかもしれない”という選択肢が、店長の頭に浮かぶかどうかだけが問題なのである。
顧客離れの“恐れがある”というだけで、多くの店長にとって“明日の顧客”が合理的な選択となる。
この店長の心理は重要なポイントだと思うので、もう少し掘り下げてみたい。
マスクに関して言えば、私は内心「マスクは直接にはウィルスに対して効果が無い」と思っている。
というのも、コロナウイルスの大きさはおよそ100nm程度、マスクの目の大きさは数μmレベルなので、マスクによってウィルスを濾し取るのは無理な話だからだ。
それでも、私は外出するとき(本心に反して)「マスクを付ける」という選択を行っている。
なぜかというと、周囲の人から「あの人はマスクを着けていない、配慮に欠けた人だ」と見られたくないからである。
ここで、本当に周囲の人がそう思うかどうかは問題ではない。
また、マスクが本当に効果があるかどうかも問題ではない。
私の頭に「周囲の人に猜疑の目を向けられるかもしれない」という選択肢が浮かぶことが問題なのだ。
思い浮かべただけで、私は「マスクを付ける」という選択肢を選ばざるを得ないのである。
多くの店長が“明日の顧客”を選ぶのも、心理的には私のマスク着用の選択に似ている。
「本当に顧客がどう思うか」が問題なのではなく、「きっと顧客はこう考えるだろう」と店長が思い浮かべることが問題なのだ。
さて、こうして多くの店長が“明日の顧客”を選択した後、転売ヤーの存在をどう考えるだろうか。
明らかに、転売ヤーはショップにとっての競合相手である。
ショップにとって、顧客が今すぐ転売ヤーから10万円のマスクを購入するより、
少しの間我慢してもらって、将来“信頼のおける”ショップで買ってもらった方がずっと良い。
そのため、ショップは「転売ヤーは、消費者の足元を見る、信頼のおけない“悪”である」と主張することになる。
つまり、ショップは「転売ヤーを“悪”にした方が都合の良い人たち」なのだ。
[3].転売ヤーは内心“自分は悪くない”と思っていたとしても、公衆の面前で謝るという選択を採用する。
では、今度は転売ヤーの立場に立って考えてみよう。
もしあなたが転売ヤーだったとして、ネットオークションで高額のマスクを売りさばいていたとする。
それがひょんなことで、あなたの友人・知人に知られたとしよう。
このとき、あなたは次の2択を迫られることになる。
(1): 上に書いたような説明を行った後、自分の無罪を主張する。
(2): 言い訳をせず、素直に謝る。
どうだろうか。
私なら“素直に謝る”方を選択する。
なぜかというと、(1)の説明を相手が受け入れてくれない、納得しない恐れが多分にあるからだ。
ここでも、(1)の説明が本当に正しいかどうかは問題ではない。
また、実際に説明した“後で”、相手が納得するか、しないかも問題ではない。
"相手が納得しないかもしれない"という恐れが転売ヤーの脳裏に浮かんだだけで、多くの転売ヤーは“素直に謝る”方を選択せざるを得ないのだ。
説明を行う“前に”、転売ヤーは手持ちの情報だけで判断を下さなければならない。
この“情報の非対称性”については、ショップの店長も、転売ヤーも、同様の状況に置かれているのである。
この転売ヤーの選択については、自分が県議会議員といったような立場にあったと想像すれば、より分かりやすい。
もし自分が議員だったなら、多くの有権者は (1), (2) の選択のどちらを受け入れるだろうか?
あるいは、「多くの有権者に受け入れてもらえるだろう」と議員が考える選択肢は、どちらだろうか。
悩むまでもなく、(2)の謝罪である。
たとえ内心、「本当は私は悪いことなどしていない」と考えていたとしてもである。
もし本意に反する言動が“悪”だというのなら、以下は全て“悪”ということになる。
・本当はマスクなど効果が無いと思っているのだが、意に反して付けるしか選択肢が無い、私の外出行動。
・本当は判で押したようなリクルートスーツなど着たくもないのだが、意に反して着るしか選択肢が無い、就活に臨む若者たち。
・本当は働きたくないのだが、意に反して働くしか選択肢が無い、サラリーマン。
・本当は仲良くしたいのだが、意に反して加担するしか選択肢が無い、クラスのいじめ。
※ 他にも例文を作ってみよう、「本当は〇〇だが、意に反して〇〇しか選択肢が無い、〇〇。」
以上の事情があるため、転売ヤーは隠れてコソコソ行動することになる。
[4].どこにも“悪”は無く、あるのは合理的選択だけだった。
以上、「もし自分が○○だったら」と想像すれば、当然の帰結であったと分かる。
どこにも“悪”は無かったのだ。
[5].その選択は最終的に、転売ヤーを利用するか、拒否するかという、消費者の行動にかかっている。
では、あなたが、私が、あるいは社会が、転売ヤーを“悪”と見なすか、そうでもないのか。
その判断は最終的に、消費者の行動にかかっている。
もしあなたや私の大多数が転売ヤーを利用したなら、それだけ転売ヤーに正義を与えたことになる。
あるいは転売ヤーを利用せず、“良心的な”ショップだけを利用したなら、ショップが正義となる。
答は、私自身、あなた自身の行動で示すことになるわけだ。
[おまけ].マスクは手作りできる。
で、私の行動なのだが、転売ヤーからもショップからも購入せず、手作りでしのぐことにした。
手ぬぐいとゴム紐でマスクができた。

ラグランジュ方程式のイメージ解釈
ラグランジュ方程式とは、解析力学を初めとする物理学の基礎を成す方程式です。
∂L( q(t), q'(t), t )/∂q(t) - d/dt{∂L( q(t), q'(t), t ) /∂q'(t) } = 0
-- wikipedia:オイラー=ラグランジュ方程式
ちょうど関数の最小値を求めたいとき「微分=0」を調べるのと同じように、
汎関数(関数の関数)の最小値を求めたいとき、このラグランジュ方程式を調べます。
ただ、「微分=0」には“谷底の傾きは平らになる”という明確なイメージが描けるのに比べて、
ラグランジュ方程式のイメージを思い描くのはかなり難しい。
数学が相当得意な人であっても、記号の字面を追うのが精一杯、というのが実情でしょう。
ラグランジュの『解析力学』という本には、イメージを助ける図が一切ありません。
「緒言」でラグランジュ自身が述べているように,この本には「図がまったく見出され」ず,必要とされるのは「代数的な操作のみ」である.
-- <翻訳> J・L・ラグランジュ『解析力学』(抄)
-- https://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/137415/1/phs_5_127.pdf
そもそも解析力学とは、
「代数的な操作こそが正当であり、幾何学的な図は本来排除されるべき補助手段に過ぎない」
という思想の産物だったのです。
この思想は現代でもなお有効で、高度抽象的な対象を前にして、私たちは
イメージ化をスッパリ諦めるか、
邪道であっても図を思い描くか、
の2択を迫られているわけです。
ラグランジュ方程式が難しいと感じる本当の理由もここにあって、
最初からイメージ化を諦めてかかった方がむしろ受け容れやすい、という側面があります。
にもかかわらず、ここではあえて邪道なイメージ化の方法を試みます。
ラグランジュさんには申し訳ないのですが、私たち凡人はイメージ化して初めて腑に落ちたと感じるからです。
ラグランジュ方程式の骨格を読み解くため、いったん“微分”という要素を棚上げし、
まず“関数の関数”という要素だけに着目しましょう。
いま、
L(t) = t^2 - 2 t
という、t の関数があったとしましょう。
ここで L の最小値を求めよと問われれば、関数 L(t) を t で微分するのが常套手段なのですが、
ここではあえて次のような見方をとります。
T(t) = t^2
U(t) = 2 t
と置いて、
L( T(t), U(t) ) = T(t) - U(t)
という“T と U の関数L”を作ります。
このとき L の最小値を求めるには、
T と U がちょうどバランスをとって等しくなる点、T' = U' を探せばよい、
ということになるでしょう。
T'(t) = 2 t
L'(t) = 2
2 t = 2 を解いて、t = 1 のとき L は最小となる。

こんな手間をかけて何が嬉しいのかというと、最小値についてのイメージが変わります。
関数 L(t) を直接 t で微分するとき、最小値とは“傾きが0となる点を探す”ということでした。
一方、L(T,U) = T - U を間接的に t で微分したとき、最小値とは“T' と U'がバランスをとって打ち消し合ったとき”という意味に変わります。
“傾きが0となる点”という見方をするなら、最小値は“点”として得られました。
一方、“バランスをとって打ち消し合う”という見方をするなら、
T'=U' を満たす点を列挙することで、最小値を“線”として得る道が拓けます。

ここに変分法 ~ 最小となる関数を求める方法 ~ のカラクリがあります。
解析力学における「ダランベールの原理」も、結局はこの“バランスをとって打ち消し合う”ことを意味しています。
運動する物体は、局所局所において、静的な力と、動的な加速(に由来する力)が打ち消し合っている。
なので、そうしたバランスを保つ点を線で結べば、運動の軌跡が自ずと浮かび上がるだろう。
これが、ラグランジュ方程式を形作るアイデアだったのです。
“バランスをとって打ち消し合う”ことを経済に例えるなら、需要と供給の均衡点のようなものです。
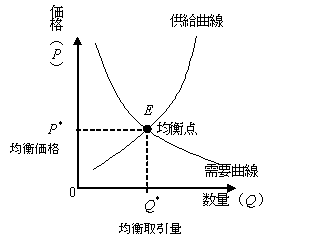
-- wikipedia:需要と供給 より引用
ラグランジアンとは、余計なエネルギーコストという意味で、経済で言うところのコストと高い親和性があります。
仮に「需給のバランスがとれた姿が実現すべき社会である」と考えるなら、
需給バランスを原理原則として、社会の姿を予言(計算)できることになるでしょう。
たとえば原料価格を横軸にとって、均衡点を線で結べば、原料価格に対する適正な生産量のグラフが描けます。
あるいはもし、消費者の満足度のようなものが数値化できれば、
満足度を横軸にとって均衡点を線で結べば、適正価格のグラフが作れるはずです。
※ 私は経済学には疎いのですが、どうも昨今の経済学(の一派)は、そういう事をやっているみたいです。
※ 『大学二回生のときに「解析力学」の講義で習ったラグランジュの方程式が、なぜかミクロ経済学の教科書にそのまま書かれているのである。』
※ * 現実と違っても数学モデルを信仰してしまう経済学者たち >> http://data11.web.fc2.com/jiyuuboueki5.html
需給バランスの例で言うと、オリジナルのグラフは横軸が「数量」となっています。
この1枚のグラフから得られる答は「均衡点」というただ1点のみであり、
それだけで終わっていたなら、需給バランスのアイデアはここまでありがたがられなかったことでしょう。
需給バランスが有用なのは、オリジナルのグラフの上にさらにもう1次元、原料価格とか、満足度とかいった、新たな変数が追加できるところにあります。
オリジナルの均衡“点”は、新たな変数 ~ 原料価格に対する“線”、あるいは満足度に対する“線”となります。
さて、だいぶ持って回した言い方となりましたが、先ほどの単純な例、
L(T,U) = T(t) - U(t) = t^2 - 2 t
に立ち返ると、そこにあったのは変数 t のみで、このままで終わっていては何のありがたみも感じられません。
変数 t の上に、新たな変数、位置 q と、速度 q' をオーバーラップさせて初めて、
・位置 q に対する均衡の線
・速度 q' に対する均衡の線
が描けるわけで、ラグランジュ方程式の真価が発揮されるのです。
※ 解析力学では、物体の位置を x と書かずに q と書くことが多いです。
※ x がいわゆる直交座標を表すのに対し、q は広く一般的な座標という気持ちが込められています。
改めて、先ほど省いてきた“微分”の要素に目を向けましょう。
ラグランジアンLを、本来の姿、
L( q(t), q'(t) )
に戻します。
つまりラグランジアン L とは、位置 q と、速度 q' の関数です。
※ 本来であれば、さらに時刻 t も含めるべきなのですが、簡単のため省略します。
冒頭に掲げたラグランジュ方程式の骨格のみを抜き出すと、こうなります。
∂L/∂q = d/dt{ ∂L/∂q' }
ラグランジアン L を「エネルギーコスト」と読み替えると、この式は、
「エネルギーコスト L に対する、位置 q の寄与と、速度 q' の寄与が均衡している」と読むことができます。
あるいは、「静的な力と動的な力が均衡している」と読むこともできるでしょう。
(そして、位置と速度が均衡しているとき、エネルギーコストは局所的に最小となる、というのがこの式の使い方です。)
ただ、式を見ると、速度 q' のある右辺には d/dt という操作が施されています。
この d/dt を、どう解釈すべきでしょうか。
最も邪道にして簡単な解釈は“約分”です。
速度 q' という記号を、ライプニッツ流の書き方 dq/dt に直してみましょう。
(どちらの書き方でも、t で微分する、という意味は同じです。)
そして、d/dt という記号は“約分”できる、とするなら、
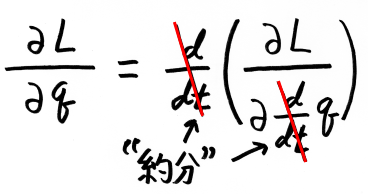
このように、ラグランジュ方程式とは(少なくとも強引な字面の上では)極めてアタリマエのことを主張していたのです。
“約分”よりもう少しまっとうな解釈は、「単位時間当たり」という操作の必然性です。
d/dt には「単位時間当たり」という意味があります。
仮に、時間がゆっくり流れているスローモーションの世界があったとしましょう。
スローモーションの世界では、時間はゆっくりになりますが、運動の軌跡は同じ形のままです。
時間がゆっくりになっても、位置 q の寄与(位置 q に依存する静的な力)は変わりません。
一方、時間がゆっくりになったとしたら、速度 q' の寄与(速度 q' に依存する動的な力)は小さくなるはずです。
それでも軌跡が同じだということは、速度 q' の寄与を、時間の流れる速さに合わせて調整しなければなりません。
どのように調整するかというと、時間の流れる速さで割ってやる、つまり「単位時間当たり」の量に換算します。
これが速度 q' の寄与 {∂L/∂q'} に d/dt という操作を施す理由です。
もし時間がゆっくり流れる世界が認められないのなら、時間の単位を変えて計算することを考えてみてください。
運動の軌跡は、秒単位で計算しようとも、分単位で計算しようとも一致するはずです。
にもかかわらず、単に {∂L/∂q'} を計算すると、秒速の方が分速の 60倍となり、静的な力 ∂L/∂q と釣り合いがとれなくなってしまいます。
(静的な力の方には、陽に単位時間が入っていないことに注意。)
方程式が成立するためには(つまり方程式の両辺の単位を合わせるには)、{∂L/∂q'} を時間の単位で割る必要があります。
※ この時間単位を揃える操作 d/dt と、そもそも速度とは位置の時間変化であった dq/dt とは、表記の上では“約分”のように打ち消し合います。
以上のお膳立てが整ったところで、ラグランジュ方程式のイメージ化を試みましょう。

まず横軸に時刻t、縦軸に物体の位置qをとり、運動の軌跡を描きます。
これに高さの軸Lを追記し、3次元のグラフを形作ります。
Lは物体の位置qに依存するので、それをq×L平面上に描きます。
q×L平面上に描かれた軌跡の傾きは、∂L/∂q を意味します。
ここまでは静的な力の話で、図の上では青色で描かれています。
次に、運動の軌跡を微分した速度q’の線をt×q平面上に重ねて描きます。
速度q’の軸は、位置qの軸とスケール(単位目盛り)が異なっているため、改めて図の右側にq’軸を付け加えました。
つまり微分したq’の線は、右側のq’軸の方を用いたt×q’平面上にあるものと考えます。
(図の上で、t×q平面とt×q’平面は重ねて描かれています。)
Lは物体の速度q’にも依存するので、それを描く平面が必要です。
図の上に、速度q’軸に直行する形で、高さ軸 d/dt(L) を付け加えましょう。
(図の上で、右端で垂直に立っている平面がq’×dt/d(L)平面となります。)
この q’×dt/d(L)平面上に描かれた軌跡の傾きは、d/dt(∂L/∂q') を意味します。
ここまでが動的な力の話で、図の上では赤色で描かれています。
こうして描いた3次元のグラフを、横方向から眺めてみましょう。
横軸にqとq’のオーバーラップ、縦軸にLとdt/d(L)がオーバーラップした、
2枚の青と赤の重なったグラフが見えることになります。
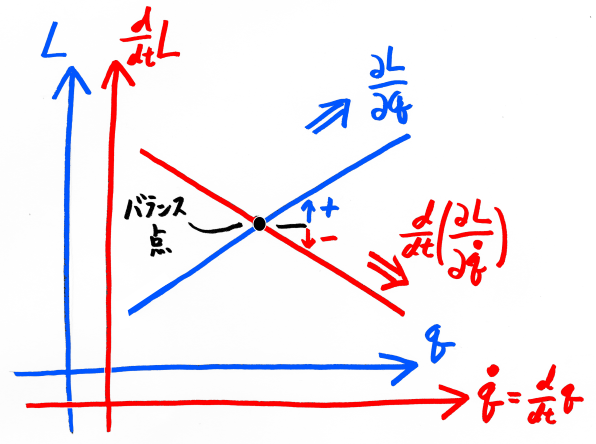
青いグラフの上には、Lに対する位置 q の寄与(位置 q に依存する静的な力)が描かれています。
赤いグラフの上には、Lに対する速度 q' の寄与(速度 q' に依存する動的な力)が描かれています。
このとき、Lを局所的に最小とするのは、2つの力の均衡点となります。
逆に、この均衡点を計算しながら辿っていくことで、もとの運動の軌跡が再現できます。
そして、均衡点を表す式とは(静的な力)=(動的な力)という形をとり、記号で書けば
∂L/∂q = d/dt{ ∂L/∂q' }
これがラグランジュ方程式です。
* まとめ *
・微分というツールを、“傾き=0”ではなく、“2つの勢力がバランスをとって打ち消し合った均衡”であると捉える。
・ラグランジアンLを、「エネルギーコスト」と読み替える。
・2つの勢力を、
(1) エネルギーコストLに対する位置 q の寄与(位置 q に依存する静的な力)
(2) エネルギーコストLに対する速度 q' の寄与(速度 q' に依存する動的な力)
に対応させる。
・(1) と (2) は同じ土俵(座標系)の上には乗らない。
なぜなら、静的な力が単位時間を含まないのに対し、動的な力は単位時間を含むからである。
そこで、動的な力の方に d/dt という操作を加え、同じ土俵に乗せる。
・こうしてできた均衡の式が、ラグランジュ方程式だ。
∂L/∂q = d/dt{ ∂L/∂q' }
最後に、以上のようなイメージ解釈は冒頭にも述べた通り、ラグランジュさんの精神からすれば邪道なのであって、
いわゆる教科書流の「代数的な操作のみ」による証明が正道であるとされています。
しかしなぜ、代数的操作は正しく、イメージ解釈は受け入れがたいのでしょうか。
天才ラグランジュさんとて人の子であり、おそらく誰よりも明確なイメージを抱いていたはずです。
そのイメージを公開しなかった理由の1つは、逆説的ですが、
『イメージは正しく人に伝わらないから』
ではないかと思うのです。
凡才である私がラグランジアンの図を描きつつ浮かんだのは、
「この図の意図は、なかなか人には伝わらないだろうな・・・」
という思いでした。
図の読み手が悪いという意味ではなく、この図では意図が描き切れていない、表現力が足りないという意味です。
もう少し具体的に言うと、“時間の流れを揃える”といった感覚を図にすることができません。
もちろん、自然言語で表すことも難しい。
インターラクティブなアニメーション、dtをビヨーンと引き延ばすと、それに伴って {∂L/∂q'} が変化するようなオブジェクトを作れば、もう少し表現できるかもしれません。
それでも完全ではありません。
勝手な想像ですが、天才ラグランジュさんは、自分の持つイメージが当時の人たちにはまず伝わらないと悟ったのではないでしょうか。
その上で、驚くべき方法 ~ 代数的操作のみによって表現する方法を開拓したのだと思うのです。
それがあまりにもすごかったものだから、後世の人がすっかり「代数的な操作のみが真実」であると信じ込んでしまった。
確かに、代数的な記号操作はイメージよりも誤解が少ないし、コピーするのも難しくはありません。
しかし、ただコピーしただけでラグランジュさんの意図が伝わったのかというと、そこには依然、大きなギャップがあるものと思うのです。
代数的操作による説明は、以下を参照。
* ラグランジアンに意味は無い >> d:id:rikunora:20090327
平均と分散の物理モデル
以下は、前エントリー「なぜ分散は2乗の和なのか」d:id:rikunora:20190409 から出たオマケの与太話。
なぜ分散は2乗なのか、と問われたとき、「分散を最も小さくする点が平均値だから」というのが1つの答でした。
この答を物理的なモデルに当てはめると、こんな絵が描けます。
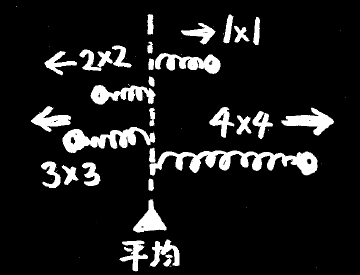
・各データと、とある1点をバネで結んだとき、1点は平均点で止まる。
このモデルで分散は、「バネに溜まったエネルギー」に対応付けられます。
分散が足し算できること(加法性)は、「エネルギー保存則」として理解できます。
ところが分散は、こんな物理モデルに当てはめることもできます。
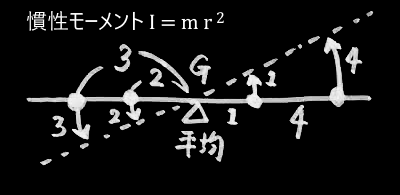
・各データに重みを付けてバランスをとったとき、重心は平均点と一致する。
このモデルの場合、分散は「慣性モーメント」に対応付けられます。
分散が足し算できること(加法性)は、「角運動量保存則」として理解できます。
以下、確率・統計入門(小針あき宏)という本からの引用。
これだけを見ていると何でもないようだが、これは‘平均の持つ意味’についての、一つの思想を物語っている。
・・・平均値をその分布の代表とする理由は、そのまわりの分散が最小ということによって特徴づけられているわけである。
ρ(x)を質量密度と考えると、分散は慣性能率に対応していることは、説明を待たないであろう。
そして自由な剛体の運動は、加えられた力をF,質量をMとするとき、
F=Mx''
によって記述される、重心の曲線運動と、
慣性能率をI,重心からの力の加えられたところまでの距離をrとすると
Fr=Iθ''
によって記述される、重心回りの回転運動によって完全に決定されるが、
どうして《重心のまわり》に回転がおこるか、というと、そのまわりの慣性能率が最小だから、に他ならない。
そして重心~平均、慣性能率~分散、の対応を見るとき、平均の持つ意味について、新たな理解が生ずるだろう。

エネルギーとは、「物理的に、時間変化に対して不変な保存量」のことです。
角運動量とは、「物理的に、角度の変化に対して不変な保存量」のことです。
物理学には“ネーターの定理”と名付けられた定理があります。
標語的に言うと、「対称性あるところに保存則がある」といった主張です。
ネーターの定理によると、
・時間並進の対称性から「エネルギー保存則」が、
・回転の対称性から「角運動量保存則」が、
・空間並進の対称性から「運動量保存則」が、
それぞれ導かれます。
ならば、分散を「運動量保存則」に結びつけるような物理モデルは無いものだろうか・・・
少し考えてみたのですが、うまいモデルは思いつきませんでした。
それもそのはず、エネルギーと角運動量が2次式なのに対し、運動量保存則は1次式なので、土台あてはまらないのです。
※ 運動量保存則は、”分散”ではなく”平均”に結びつけられます。
※ 平均は、確かに平衡移動について対称、一斉にゲタを履かせても不変ですが、あまりにもアタリマエなので意識されません。
話はこれだけなのですが、以上は何も分散だけに限った話ではなく、2次式で表されるような量全般に言えるように思えます。
もともと2次式に当てはまるような量であれば何であれ、
エネルギーや角運動量に関連付いたもっともらしい物理モデルとして表される、ということです。
一般に、理解の仕方や解釈は、個々人の感性やセンス、才能といったものに委ねられると言われがちです。
しかし、この分散の物理モデルを見て思うことは、
「思考の筋道とは全くの自由奔放ではなくて、自ずと規定されている」ということです。
不自然さを感じさせない発想は、文字通り“物の理”に叶っているのです。
そうした“物の理”に叶った発想だけが、分かりやすく、人に伝えやすく、結果的に生き残るのではないか。
そんな風に思えるのです。

- 作者: 小針アキ宏
- 出版社/メーカー: 岩波書店
- 発売日: 1973/05/31
- メディア: 単行本
- 購入: 5人 クリック: 130回
- この商品を含むブログ (23件) を見る
なぜ分散は2乗の和なのか
Q.なぜ分散は、単純な差(偏差の絶対値)ではなく、差の2乗を計算するのか?
A.分散を最も小さくする点が平均値だから。(単純な差を最も小さくする点は中央値となる。)
“分散”というキーワードは統計学の基礎中の基礎であり、どんな教科書にも“平均”の次くらいに載っていることがらです。
しかしながら、いきなり登場する“分散”の意味が分からず、統計学の入り口で挫折する人は少なくありません。
偏差の2乗の平均、つまり、各値と平均との差の2乗の平均を分散といい、
分散の平方根の正の方を標準偏差という。
統計で、ちらばりを表すものとして、標準偏差や分散が多く用いられる。
-- 高校の教科書(啓林館)より.
教科書にはこのように書かれているのですが、これで分かった気になるでしょうか。
・なぜ、差の2乗を計算するのか?
・差そのものであってはいけないのか?
・なぜ、分散と標準偏差の2種類があるのか?
最後の疑問については「分散が2乗した結果なので、元の単位に戻すために平方根をとる必要がある」のだと説明されます。
(標準偏差) = √(分散)
だとすると、そもそも値を2種類作らなければならなかった理由は2乗を計算するからであって、
最初から差そのものを採用していれば1種類で済んだはずです。
各データと平均値との差のことを「偏差」と言います。
分散とは、偏差を2乗した値の平均のことです。
一方、偏差の値そのもの(絶対値)の平均は「平均偏差」と呼ばれています。
分散(と標準偏差)に比べて、平均偏差はあまり有名ではありませんし、全ての教科書に載っているわけでもありません。
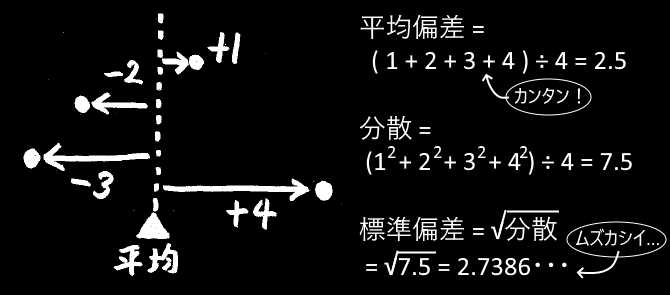
もし何の予備知識も無しに「ばらつきを数字で示せ」と言われたなら、
データの差そのものを持ってくる平均偏差の方がよほど自然に思えます。
なのになぜ、今日の統計では、ややこしい分散(と標準偏差)の方が主流なのでしょうか。
歴史を振り返ってみると、偏差の2乗が一般化する以前に、差そのものをばらつきの指標と捉えていた時期がありました。
例えばラプラスは、差そのものを誤差損失の指標として扱っていたという経緯があります。
はっきりと2乗を指標とするようになったのは、ガウスの登場以降のことなのです。
Laplaceはこのことを同じような方法で考察した。しかし彼は、つねに正として扱われる誤差自身を損失の量として選んだ。
-- ガウス誤差論より.
■ 最小2乗法のこころ
ではなぜ、ガウスは2乗を考えたのか。
その心を知るには、ガウスのお家芸である“最小2乗法”をひもとくのが早道です。
最小2乗法とは、誤差を含んだデータに対して、もっともよく当てはまる関係を見出す方法です。
例えば、とあるグループの身長と体重のデータが、こんな風だったとしましょう。
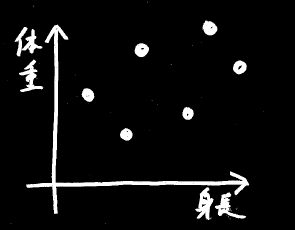
ここで「身長が高いほど体重が重い」という関係を1本の直線で示すには、どのように線を引くのがもっとも合理的でしょうか。
最小2乗法では、次のように考えます。
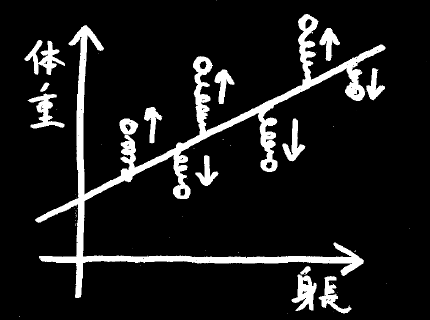
一本の棒と、それぞれのデータの間をバネで結んで引っ張ると、棒はほどよいところに落ち着きます。
この落ち着いた先の状態を「もっとも当てはまりが良い」と見なすのが、最小2乗法の考え方です。
なぜ2乗なのかというと、バネは引っ張れば引っ張るほど、長さに比例した力がかかるからです。
バネの長さを2倍に引き伸ばすには、
・長さが2倍
・力も2倍
合わせて2×2=4倍のエネルギーが必要です。
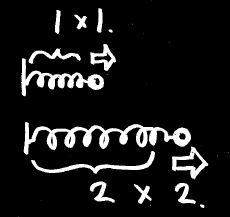
これが2乗の由来です。
最小2乗法とは、つまり「バネに溜まったエネルギーが最小となる位置を探す方法」のことだったのです。
* ∫ニョロっと伸びるはエネルギー、バネは答を知っている
>> http://miku.motion.ne.jp/multi/01_MinSquare.html
いま、2次元のグラフで見た方法を、さらに単純化して1次元としてみましょう。
複数個のデータと、自由に動かせる、とある1点をバネで結んだとしたら、とある1点はどこに落ち着くか。
落ち着く先は、ちょうどデータの平均値となります。

※ 2次元の場合、当てはめた直線(回帰直線)は必ず平均値を通ります。
平均値とは、「バネに溜まったエネルギーが最小となる点」のことだったのです。
そして「バネに溜まったエネルギー」とは、各データと平均との差の2乗、つまり分散に比例しています。
かくして手元のデータから、もっとも当てはまりの良い点を探そうと考えたとき、分散の最小化というアイデアに導かれるわけです。
■ 分散の加法性
ここで1つクイズ。
『厚さが平均1cmの月刊誌を1年分積み上げたら、高さは平均で何cmになるか?』
答は当然、12cm。
では次に、
『その雑誌のばらつきは±1mmだった。1年分積み上げたとき、ばらつきは±何mmになるか?』
ここでの「ばらつきが±1mm」の意味ですが、話を単純化して、雑誌の厚さには 9mm と 11mm の2種類しか無くて、
その2種類が毎月ランダムに発行されるものとしましょう。
答の選択肢:1年分のばらつきは・・・
(a) ±12mm、 ±1mm × 12ヶ月だから。
(b) ±0mm、 +と-が打ち消し合って0になるので。
(c) ±12mm でも ±0mm でもない、中途半端な数。
・・・ちょっと考えてみよう・・・
正解は (c)。
試しに ±1 の乱数を12個、何回も足し合わせた平均の絶対値をとると 2.7mm くらいの値となります。
(2項係数を用いて詳しく計算すると 2.70703125... といった値になります。)
つまり、ばらつきに関しては単純な足し算ができないということです。
何とか上手い具合に“ばらつきの足し算”ができないものだろうか・・・
そこで編み出されたのが「2乗すれば足し算できる」というアイデアです。
±1mm の乱数が12個あったとして、それぞれをただ足し合わせるのではなく、2乗して足し合わせてみましょう。
(±1)^2 + (±1)^2 + (±1)^2 + ・・・ ±1)^2 = 12
これなら個々のばらつきがプラスであってもマイナスであっても、合計は確実に+12となるでしょう。
このように、2乗した値によってばらつきを数えたのが、分散という指標だったのです。
・雑誌1冊あたりの分散 = 1
・12冊積み重ねた全体の分散 = 12
※12冊のサンプルがたくさんあったときの分散。つまり毎年の雑誌の山をたくさん並べたときのばらつき。
分散は足し算することができる。
この性質を分散の加法性と言うことがあります。
むしろ、足し算ができるような指標を探したところ、うまくいったのが分散であった、というのが実情でしょう。
では、雑誌1年分の分散が12だったとして、実際に雑誌の山の高さは±何mm程度なのでしょうか。
そこで分散の平方根をとって、元の次元に戻したのが標準偏差です。
今の場合、
(標準偏差) = √12 = 3.46mm
といった値となります。
※ 標準偏差 3.46mm は、少し上に書いた平均偏差 2.71mm とは異なります。
※ 標準偏差は偏差2乗和の平均、平均偏差は偏差絶対値の平均です ← しつこいようですが、ここんとこよく間違うので。
■ 分散のエネルギー解釈
・分散とは「バネに溜まったエネルギー」のこと。
・分散とは「足し算できるように」編み出されたばらつきの指標。
この2つが「なぜ分散が2乗なのか」についての主な答になると思います。
さらに穿った見方をするならば、この2つは別々の事柄ではなく、共通の内容を含んでいると解釈することもできるでしょう。
そもそもエネルギーとは何だったかといえば、
「物理的に、時間変化に対して不変な保存量」
のことでした。
何らかのデータ操作について、例えば上に述べた“バネと棒”のような物理的なモデルを考えたなら、
そのモデル上で足し算できる保存量は、自ずとエネルギーに対応付けられるはずです。
こと分散については、「変位の2乗で溜まるエネルギーのような保存量」というイメージで把握できると思います。
この線で標準偏差に解釈を加えるなら、
「各データにエネルギーを等しく分配したとき、1個あたりのデータが変位する大きさ」
ということになります。
■ 最小絶対値法ではダメなのか
以上、分散(と標準偏差)が、いかにばらつきの指標として合理的であるかを見てきました。
ならば、ばらつきの指標は分散だけが唯一無二であり、それ以外にはあり得ないのでしょうか。
実はそうでも無いのです。
分散は、一般的には最も優れた指標なのですが、場合によっては分散以外の指標が有用なこともあります。
先に、分散 ~ 最小2乗法に基づいてデータの当てはまりを考えたのですが、
次に、偏差の値そのもの ~ “最小絶対値法”に基づくデータの当てはまりを考えてみましょう。
1次元の場合、もしデータが2つだけだったなら、
もっとも当てはまりの良い点は、2つのデータの間のどこでも良いことになります。
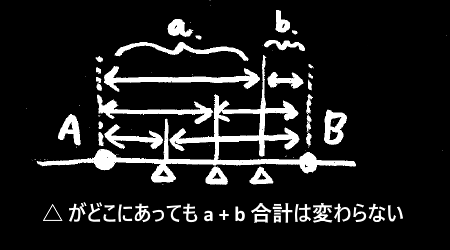
このように最小絶対値法には、結果が1点に落ち着かないといった不定性があります。
これが最小絶対値法 ~ 平均偏差が流行らない1つの理由です。
データの数をもう少し増やしてみましょう。
もしデータが5つだったなら、最小絶対値法によるもっとも当てはまりの良い点は、中央の3番目の点になります。
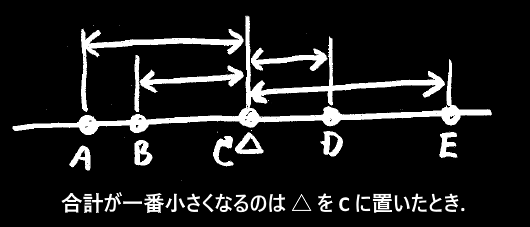
平均偏差を基準に考えたなら、
・データが奇数個の場合、順位が中央の点となる。
・データが偶数個の場合、順位が中央に最も近い2点の間のどこでもよい。
つまりこれは「中央値」ということです。
※ 中央値の定義としては、データが偶数個の場合、中央に最も近い2点のちょうど中間(平均)となります。
・分散 :偏差の2乗の平均値 : 最小2乗法 : 最小となる点は平均値
・平均偏差 :偏差の絶対値の平均値 : 最小絶対値法 : 最小となる点は中央値
このように対比させてみれば、決して“分散が優れていて、平均偏差が劣っている”わけでは無いのだと分かるでしょう。
さらに興味深いのは、2次元の場合です。
一般によく用いられている最小2乗法ではなく、最小絶対値法による直線の当てはめも、それはそれでアリなのです。
* 最小絶対値法による回帰分析
>> http://www.orsj.or.jp/~archive/pdf/e_mag/Vol.40_02_261.pdf
* 最小二乗と最小絶対値:ロバスト回帰で外れ値分析
>>https://biolab.sakura.ne.jp/robust-regression.html
* Excelで操る!誤差の絶対値和を最小にする
>> http://godfoot.world.coocan.jp/Abs_Min.htm
最初のリンク先に、ラプラスの考えた最小絶対値に基づく方法が載っていました。
この回帰分析規準(1)を最良のものと考え,そのアルゴリズムを最初に提案したのはLaplace[PiereSimmonMarquisdeLaplace,1749-1827]である。
リンク先の説明を参考に、ラプラスの考えた直線当てはめの方法を試してみました。
・原点を通る直線を考える。
・各データを傾きの順番に並べる Y1/X1 >= Y2/X2 >= Y3/X3 ・・・ Yn/Xn
・X1 + X2 + X3 ・・・ + Xr-1 < Xr + Xr+1 + Xr+2 ・・・ + Xn かつ
X1 + X2 + X3 ・・・ + Xr > Xr+1 + Xr+2 ・・・ + Xn となる r を探す。
つまり、傾きの大きい方から X を合計していって、合計値が残りの合計をちょうど越える番号 r を探す。
・最も当てはまりのよい傾きとして、Yr/Xr を採用する。
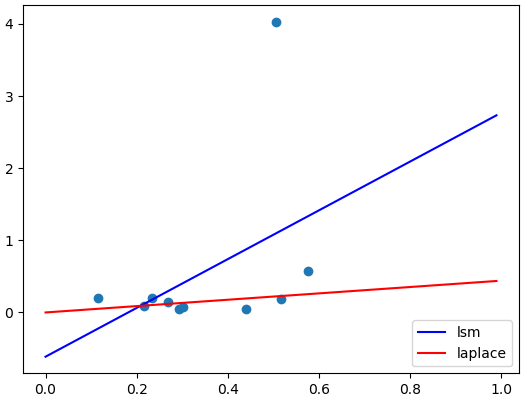
これは当てはめ結果の1例です。
青線が最小2乗法、赤線がラプラスの考えた最小絶対値法です。
この例のように極端な外れ値が混じっていた場合、最小2乗法は外れ値に引っ張られるため当てはまりが悪くなります。
中央値が平均値に比べて外れ値に強いように、最小絶対値法には外れ値に対して頑健な性質があります。
回帰分析のあてあまり評価の指標として、RMSE, または MAE という値がよく用いられます。
これらは何なのかというと、分散と平均偏差、あるいは平均値と中央値、という並びに位置づけられるものです。
* 平均平方二乗誤差 = RMSE(Root Mean Square Error)
・RMSE の最小化 = 二乗誤差の最小化 = 誤差に正規分布を仮定した場合の最尤推定
* 平均絶対誤差 = MAE(Mean Absolute Error)
・MAE の最小化 = 絶対誤差の最小化 = 誤差にラプラス分布を仮定した場合の最尤推定
-- 精度評価指標と回帰モデルの評価
>> https://funatsu-lab.github.io/open-course-ware/basic-theory/accuracy-index/
あるいは最近流行りの機械学習に登場する L1正則化(Lasso), L2正則化(Ridge) といったキーワードも、やはりこれらの概念の延長上に位置づけられます。
■ ガウス誤差論より
なぜ2乗なのか、その源流を遡ると、ガウスの誤差論にたどり着きます。

確かに2乗は優れた概念なのだが、ならば2乗を支える根拠・原理は何なのか。2乗以外の概念はあり得ないのか。
私は長らくこの疑問を抱いてきたのですが、元祖ガウスの言葉にようやく答を見たように思います。
今さらですが、(推測)統計学とはデータから帰納的に導かれるものであり、
他の数学のように原理原則から演繹的に導かれるものではありません。
その意味で、2乗が唯一絶対の方法では無かったのです。
ただ、いったん2乗を離れて他のあらゆる方法と比べてみると、改めて2乗こそが最も単純で適していると認めざるを得ません。
これが分散を2乗で数える理由であり、今日に至るまで統計学の根底に流れ続ける基盤だったのです。

- 作者: カール・F.ガウス,Carl Friedrich Gauss,飛田武幸,石川耕春
- 出版社/メーカー: 紀伊國屋書店
- 発売日: 1981/05/01
- メディア: 単行本
- この商品を含むブログを見る
# -*- coding: utf-8 -*- # # Laplaceの絶対値回帰 import numpy as np import matplotlib.pyplot as plt # 直線回帰を行う def fit_line(x, y): mx = np.mean(x) my = np.mean(y) myx = np.mean(y * x) mxx = np.mean(x * x) w0 = (myx - my * mx ) / (mxx - mx ** 2) w1 = my - w0 * mx return ( w0, w1 ) # 適当な直線+乱数データを用意 N_SAMPLE = 10 ALPHA = 0.0 # 切片は0に限定する BETA = 0.3 EPS = 0.1 X = np.random.rand(N_SAMPLE) # Y = ALPHA + BETA * X + np.random.normal(0, EPS, N_SAMPLE) # 正規乱数 # Y = ALPHA + BETA * X + EPS * (np.random.rand(N_SAMPLE) - 0.5) # 一様乱数 Y = ALPHA + BETA * X + EPS * np.random.standard_cauchy(size=N_SAMPLE) # コーシー分布 # この場合、Laplace回帰はけっこういい感じだ # Y = ALPHA + BETA * X + np.random.laplace(loc=0.0, scale=EPS, size=N_SAMPLE) # ラプラス分布 # Laplace回帰が最尤値になるという。 #### # まずは普通の線形回帰をやってみよう lin, seg = fit_line( X, Y ) print( "線形回帰の傾き,切片 = {:.4f}, {:04f}".format( lin, seg ) ) #### # 以下、Laplaceの考えた方法で回帰をやってみる YperX =Y / X # 個々の点の傾きリスト Slp_index = {} # index->傾きリストを作る for idx in range(N_SAMPLE): Slp_index[idx] = YperX[idx] # 傾きの値で降順にソートする x_list = [] idx_list = [] for key, val in sorted(Slp_index.items(), key=lambda x: -x[1]): # print( "{{ {} : {} }}, X={}".format( key, val, X[key] ) ) idx_list.append(key) x_list.append( X[key] ) # Xの前半の合計値が後半の合計値を越える境界を探す r_index = 0 for r in range( N_SAMPLE+1 ): pre = x_list[ 0 : r ] # 前半 post = x_list[ r : len(x_list)+1 ] # 後半 if sum(pre) >= sum(post): # print( "Pre:", pre, "len=", len(pre) ) # print( "Post:", post, "len=", len(post) ) r_index = r -1 # インデックスなので1引く。 break x_esti = idx_list[ r_index ] # print( "x_ans={}, X={}, YperX={}".format( x_ans, X[x_esti], YperX[x_esti] ) ) lap = YperX[x_esti] print( "Laplace回帰の傾き = {:.4f}".format( lap ) ) # グラフ出力 xlist = np.arange(0, 1, 0.01) # 0.01単位で細かくプロットし、線として出力させる ylist_lsq = [ (lin * x + seg) for x in xlist ] # 線形回帰 ylist_lap = [ (lap * x) for x in xlist ] # Laplaceによる回帰 plt.plot(X, Y, 'o') # 元データ plt.plot(xlist, ylist_lsq, color="blue", label="lsm") # 線形回帰 plt.plot(xlist, ylist_lap, color="red", label="laplace") # Laplaceによる回帰 plt.legend(loc='lower right') plt.show()

