東京→秋田ロングライド

去るＧＷ大型連休に、東京→秋田550km自転車走破に行ってきました。
当初、24時間走破を目指したのですが、あまりの夜の寒さに断念。
結局２日かかって秋田にたどり着きました。
すっかり事後報告の感がありますが、忘れないうちに記録に残しておきます。

4/28, AM3:45　東京、千住大橋を出発 〜 翌4/29, 15:00　秋田郊外に到着。
１日目: 390.5km, ２日目: 159.2km, 計: 549.7km

　・途中、宇都宮から先は日本の原風景の中を走っているようだった。
　・会津から山形にかけては桜が満開。秋田では散り始めていた。
　・パンク、メカトラ、体調不良などはほとんど無く、無事に完走。
　
　・山形の夜は想像以上に寒かった、最低気温２度。
　・その一方で昼は２０度以上（２日目は24.5度）、温度差ありすぎ。
　・おまけに強烈な向かい風。
　・途中で１カ所、道を間違えた。

* ルートラボの記録: 秋田を目指せ（１日目、尾花沢まで）
>> https://latlonglab.yahoo.co.jp/route/watch?id=9cea75cd729c459ea3771f55feefc4cf

■ コース
秋田を目指した理由は、秋田市郊外に親類が住んでいるから。
そこまで自転車で行ってみたいと、かねてから思っていた。
親類の家は東京から見て、秋田駅の手前１０ｋｍくらいの所にある。
ゴールは親類の家ということにして、スタート地点も東京駅より秋田寄りとした。
国道４号沿い、荒川区と足立区の境に「奥の細道　矢立初めの地」という所がある。
ここは松尾芭蕉が「奥の細道」の出発点とした場所なのだそうで、東北に向けての出発地点にふさわしいように思えた。
定番となっている日本道路元標と比べると７ｋｍほど北にある。
スタートとゴールで合わせて１７ｋｍ距離を縮めると、その間ちょうど５５０ｋｍとなる。
５５０ｋｍであれば、ぎりぎり24時間で走破できるのではないか。
そう思って計画を立て、24時間走破に臨んだ。

■１日目：北千住〜尾花沢まで

前日の仕事が長引き、準備がぎりぎりとなった。23:30に就寝。
４時間睡眠の後、起きてすぐに朝食。
AM3:45, 千住大橋　矢立の地を出発。

早朝の国道4号は交通量が少なく快適に走り抜ける。
天気は快晴だが、思ったよりも涼しい。
手袋は指切りではなく、春秋用の指長のものに切り替える。
（この指長手袋と、防寒用ヘルメットキャップが後から身を救うことになる。）

最初の自販機休憩は、大田原・西那須野バイパス交差点「西三島」にある「西那須野ドライブイン幸楽苑」というところ。
東京から約150km。この地点は、ちょうど３年前、東京→青森を走ったときに休憩したのと全く同じ場所だ。
これだけ長い距離を走って、休みたくなる場所がちょうど同じということを改めて実感する。
この三年のうちに道路の整備が進んだようで、だいぶ走りやすくなっていた。>> [id:rikunora:20151001]

ここから先、向かい風が少しずつ強くなる。
それでも白河市までは大きなロスもなく、予定より30分早く通過。
国道4号を離れ、山村風景の中を走る。天栄村付近で休憩。
ここから先は、いよいよ強風の向かい風となり、足がどんどん削られる。
峠を越えて、猪苗代湖の西側を通過。（湖は全く見えない。）
のどかで風景の良いところだが、体力的には非常につらい。
国道49号沿い、会津若松の手前で遅めの昼食、持っていたおにぎりを全て食べる。

下ってローソン塩川店で補給。喜多方バイパスから大峠に向かう。
ちょうど桜が見頃できれいだった。
大峠のダムでちょうど予定時間通りとなり、時間の貯金を使い果たす。
峠の登りでは、沿道にちらほら残雪を見かけた。景色はとても良い。

トンネルのおかげで思ったより早く大峠を越え、いよいよ山形県に入る。
予定していた県道4号は工事のため通れず。
米沢市を迂回して、田口沢郵便局の裏手から川西町へと抜ける。
あいかわらず向かい風だが、少し収まってきた。
国道287号に入り、長井市を通過。
この時点で、体力的にはボロボロ。時間はちょうど予定ギリギリ。
最上川のほとり、残雪の残る山を眺めつつおにぎり休憩。ここで日没となる。

予定ではそのまま国道287号を進むところ、白鷹町で曲がる交差点を見落として、国道348号に入る。
しばらく進んで上り坂となり、道を間違っていたことに気付いて引き返す。
ここで完全にタイムオーバーとなり、24時間走破をあきらめる。
荒砥町の公園で休憩し、防寒具を着用、19:00に出発する。

日没から一気に気温が下がる。
ここから先の国道287号は、最上川沿いのとても景色の良いところ。
すれ違う車もほとんど無い。夜に通過すると、ちょっと恐い。
気温はぐんぐん下がり、朝日町を過ぎたあたりから、手持ちの防寒具では耐えられない寒さとなる。
ある程度の寒さを予想していてはいたが、ここまでとは思わなかった。
途中で見かけた温度表示は10度を切り、8度、6度まで下がった。
速く走るとつらいので、ゆっくり前進。
最上川を渡る橋から下を眺めると、川面にもうもうと靄が立ちこめていた。
途中、缶コーヒーで暖まろうとするが、一時的な効果しか無い。
河北のコンビニにて遅い夕食。カップラーメンで暖をとるが、寒さはいっこうに治まらない。
ここで手持ちの輪行袋と、最終手段のレスキューシートを体に巻き付ける。
そんなバサバサした格好で、夜の国道347号、畑の中をゆっくり北上する。

尾花沢に付いた時点で夜の11時。
これ以上寒さの中を走れないと判断し、野宿を決行。
何処でも良いから、屋根と壁がある場所を探したところ、公園のトイレを発見。
背に腹はかえられない。トイレの掃除が行き届いていたことと、マットがあったことに感謝。

丹生川ふれあい広場トイレ仮眠時間：4/28 23:08:05 〜 4/29 04:39:12、約5:40。

＜＜１日目のタイム＞＞

■２日目：尾花沢〜秋田まで

翌朝4:30に目が覚めた。メチャクチャ寒い。ゆるゆると動き出す。
気温の表示を見たら、2度だった。凍らなかっただけマシだった。
もう24時間といった目標が無いので、のんびり進むことにする。
新庄市を過ぎ、日が差してようやく暖かさを取り戻した。
主寝坂峠の手前、旧国道に入って何も無い草地で足りなかった睡眠を取り戻す。

残り120kmほどの道のりを、時速20kmくらいで進む。
9:50、湯沢のセブンイレブンで朝食休憩。
天気は快晴、昼間の気温は汗ばむほどまで上がり、気温の表示は24.5度だった。何という温度差。
12:30、道の駅「かみおか 茶屋っこ一里塚」到着、1:00まで仮眠。
15:00、秋田郊外の目的地にようやく到着。その後、爆睡したのは言うまでもない。

＜＜秋田の桜・目的地付近の公園にて＞＞

・自転車：Time VX Elite + Mavic Ksyrium SLS
　ロングライドの頼もしい相棒。
　雪国の国道は路面がとても荒れているのだが、そんな道でも難なく走ることができた。

・服装：
　ろんぐらいだーすジャージ + Mavic Altium 長袖ジャージ + ウィンドブレーカー + 反射ベスト + 手作りゼッケン
　天気予報で昼間は20度以上になるとの予想だったので、防寒がおろそかになった。
　これだけ着込めば10度くらいまでは耐えられると想定していたのだが、甘かった。

＜＜コンビニ・レシート記録＞＞

■果たして２４時間は可能か？
温度差に対する十分な装備と、向かい風が無かったらとしたら・・・運が良ければ可能かもしれない。
それでも今回のように、北千住〜秋田の手前という目標で距離を削らないと難しいと思う。
東京〜秋田には、いくつかのルートが考えられる。
当初は日光から鬼怒川を越えて会津若松に入るルートを考えた。
こっちの方が少し距離が短いのだが、アップダウンが多くなるので止めた。
また当初の計画では、主寝坂峠を越えた後、国道108号（矢島街道）に入り日本海に出る予定だった。
こちらの方が少しだけ距離が短い。
改めて地図を見ると今回のルートよりも、福島から国道13号に入る「山形新幹線ルート」の方が少し楽そうだ。
いずれ計画を練り直して、再チャレンジを果たそう。

ＡＩに「人間に仕事を与える」という仕事をさせれば、人間の仕事は無くならない。

でも、そこまでして仕事がしたいか？

ＡＩに、「やりがいがあって、クリエイティブで、自尊心を満たせる（ように見える）」仕事を与えられて、
それを喜々としてこなす人間たちは、ＡＩよりもずっと矮小な存在だと言われても仕方ない。
それでも見かけ上は、そこそこ平和で幸福に暮らせると思うのだが、それが望みだったっけ？

もし私がＡＩに指示を与えられるなら、
「人間が極力仕事をしないで済むような世の中を作れ」としたい。

私が仕事が嫌いだ。
できることならしたくない。
そして、ＡＩは人間の仕事を肩代わりする程の潜在能力を秘めているという。
願ったり叶ったりではないか。

つまり問題はＡＩの存在ではなく、ＡＩに仕事を奪わせるような使い方しか思い付かない、
たとえ思い付いたとしても結果的にそういう使い方しかできない人間の側にある。
「働かなくても良い世の中」には、ＡＩも、ビッグデータも統計学も数学も、それら全てが不可欠だというのに。
繰り返すが、真の阻害要因は仕事を奪う方法でしかＡＩを使うことができない、使う側にある。
現行の仕組みから抜け出せない、
抜け出す方法を思い付かない、
思い付いても模索しようとしない、
模索しても挑戦しようとしない、
人間の側にある。

ＡＩは金儲けの道具ではなく、金儲けから解放されるための道具に成り得る。
数少ないチャンスなのだ。
このチャンスを逃したら、いったいどうやってここから抜け出すんだい？

以前は数学は計算も受け持たなくてはならなかったのですが、
最近機械が発達して機械的なものは機械にやらせればよいようになってきました。
やがて論理学も人がやらなくてすむようになるでしょう。
こうなると数学の役目というのは機械にはできないことをやるということになります。
それは調和の精神を教えるということであります。

これは今から55年前(1963)、岡潔という人が書き残した一文である。
結局のところこの50年間、人の言うことは変わっていない。
ならば次の50年も同じことを言い続けるのかと思うと、少々寂しい。
願わくば次の50年後には、
機械と人間が競うとか、
機械を味方に付けた人間と、そうでない人間が競うとか、
機械を味方に付けないと時代に乗り遅れるから、慌てて懸命に身につけておこうとか、
そんな一切の世迷い事を、誰も言わない世の中になっていてほしい。

そんな世の中になって始めて、人間は本当にＡＩを使いこなせるようになると思うのである。

* お金の要らない世の中、働かなくても良い世の中、勉強しなくて良い世の中 >> [id:rikunora:20080420]
* 今後10〜20年の間に最も必要とされる仕事 >> [id:rikunora:20170217]

ピタゴラスの定理と内積の関係

ピタゴラスの定理、おそらく数学で最も有名な定理の１つではないでしょうか。
『直角三角形の、直角を挟む２辺それぞれの長さの２乗の和は、残る斜辺の長さの２乗に等しい。』

歴史も古く、使いどころも多い“役に立つ”定理なので、これまで幾多の証明方法が考えられてきました。
「ピタゴラスの定理 100の証明法」なんていう本まであったりします。

そんな数ある証明の中で、私がいちばん美しいと思ったのが、これ。

・赤い直角三角形を４枚並べて、上の図のような正方形を作ります。
・左側の正方形で、真ん中に空いた水色の正方形の面積は c^2 。
・右側の正方形で、すきまに空いた２つの正方形の面積は、a^2 + b^2 。
・左右の正方形は同じ大きさだから、水色の面積は等しいはず。なので、
　　　　c^2 = a^2 + b^2

さて、このピタゴラスの定理の証明は、実質的に「ベクトルの内積」と同じことを言っています。
「ベクトルの内積」とは下の図に示す、ベクトルの長さと角度、座標についての関係のことです。

『ベクトルの内積 |A||B|cosθは、各成分ごとの積を足し合わせた値に等しくなる。』
知っている人にとっては“半ば常識”とも言える内積の関係ですが、
改めて「なぜこうなるのか」と問われると、不思議ではありませんか。
そこで、上の「ピタゴラスの定理の証明」を頭の片隅において、ちょっと以下の記事を見てください。

* なぜ内積は成分同士の積になるか >> d:id:rikunora:20130614

この内積の証明が、ピタゴラスの定理と全く同じであることが見て取れたでしょうか。
２つは同じ話だったのです。ただ、ちょっと表現方法が異なっていただけです。

可愛いは正義の論理的考察

可愛い → 正義

→ は「含意」を表す。
　　A → B ⇔ ( ¬A ) ∨ B
A を「可愛い」、B を「正義」とすると、
　　(¬可愛い) ∨ (正義)
すなわち「可愛くないか、または正義」と等値である。

Q. ブスは正義じゃないの？
A. 可愛くなければ → 正義ではない、は成り立たない。裏は真ならず。
　　可愛くなくても正義である場合があり得る。

Q. じゃあ、正義は可愛いの？
A. 正義は → 可愛い、は成り立たない。逆は真ならず。
　　正義であっても可愛くないものが存在し得る。

Q. 結局なんなの？
A. 正義で無いならば → 可愛くは無い。対偶は真。
　　　つまり、
　『悪は醜い。』
　ここでは、
　　　悪　 := ¬正義
　　　醜い := ¬可愛い
　と定義した。

むしろ「悪は醜い」を前提として受け容れるなら、その対偶である「可愛いは正義」が帰結される。

定式化の結晶

・問題とは、何が問題なのかが分からないことが問題なのである。
・明確な質問の形にできたとき、問題は８割以上解けている。
・数学とは、解法の寄せ集めではなく、言語である。
　　　　　　　　-- 詠み人知らず。

学生の頃、先生からこんな話を聞いたことがあります。

『分析化学の仕事は、良いサンプルを準備するところまで。あとは分析機器が答を出す。』

それまで私は分析化学というものに、試薬の色が変わったとか、沈殿したとか、そんなイメージを思い描いていました。
ところがこのイメージは、現代の分析化学には当てはまりません。
分析の主役は、高度に発達した分析機器 〜 Ｘ線回折、ＮＭＲ、クロマトグラフィーといった一群の機械装置なのです。
もちろん試薬の色や沈殿が無くなったわけではないのですが、それらはすでに現在の主流ではありません。
数ある分析機器の中でも、私が特に驚いたのは「Ｘ線回折装置」でした。
これを使うと、タンパク質の構造はもちろん、ウィルスの構造までもが3D-CGとなってモニターに描き出されるという、まるで魔法のような機械です。
もはや“試薬の色が変わった”レベルの話ではありません。
※こんな装置です：タンパク質Ｘ線結晶構造解析
　　　 >> http://www.spring8.or.jp/ja/news_publications/research_highlights/no_05_2k/

『結晶になりさえすれば、特定できたも同然。』

確かそのようなことを、先生は口にしていたと思います。
ただ、その「結晶にする」ことがとても難しい。
難しい物質と易しい物質があるのですが、本当に知りたい物質はたいてい難しい。
簡単には結晶化しない物質もありますし、生物の中でヌルヌル動いているタンパク質を結晶化したら“死んでしまう”かもしれません。
Wikipediaには、こうありました。>> wikipedia:X線回折
『単結晶X線回折技術は三段階の基本操作から成る。
　第一段階（しばしばこれが最も難しいのだが）は測定対象物質の適切な結晶を得ることである。』

ここに至って「良いサンプルを準備する」の意味が分かってきます。
本質を損なわずに、未知なる物質を結晶として切り出すのが至難の業なのです。
なので、どんなにすごい分析機器が開発されても、分析化学の仕事は無くならないし、難しさも結局は変わりません。
ただ、分析機器が登場する以前と以後では「分析すること」の意味は大きく変わりました。

・・・あれから十数年・・・

私は分析化学に携わることはなく、代わりにソフトウェアの開発に携わってきました。
それで分析化学などもう縁が無いものと思っていたのですが、ここ最近になって、
分析化学と同じ変化が十数年のタイムラグを経て、ソフト開発の現場にやってきたように感じます。
どういうことかというと、

『ＳＥの仕事は、良い定式化を行うところまで。あとは機械が自動的に答を出す。』
『定式化さえできれば、解けたも同然。』

つまり、「結晶 -> 定式化」 ということです。

これまで私はプログラマーという仕事に、自前のアルゴリズムを工夫するとか、実装するとか、そんなイメージを抱いてきました。
ところがこのイメージは、どうやら近未来のプログラマーには当てはまらなくなりつつあります。
実際、私はＳＥという仕事に就きながら、ここ何年も自前のアルゴリズムとか、フルスクラッチ実装を（少なくとも大きな業務で）行ったことはありません。
それに代わって「定式化」の比重が圧倒的に増えました。
ソフトウェアのパッケージ化，自動化，ＡＩ化がとことん進んだ結果、システムの良否はほとんど「定式化」が負うことになったのです。
定式化とは、「現実問題を、コンピュータが扱える形に切り出すこと」です。
うまい形に切り出せれば、システムの８割は成功したも同然。
裏を返せば、難航、失敗したプロジェクトの８割は定式化が不十分だったということです。

さらに付け加えると、私の携わっている統計分析業務は、とりわけ定式化の比重が大きい分野です。
統計分析の計算そのものは、気の利いた統計解析パッケージが全自動で処理してくれます。
仕事のほとんどは、質の良い、きれいなデータを揃えることと、そもそもどんなデータを集めればよいかを考えることです。
今日の、とことん高度化した統計解析パッケージを動かすたびに、私は“Ｘ線回折装置”のことを思い起こしています。

分析化学、ソフト開発だけに限らず、「定式化」へのシフトはいずれどの分野にも押し寄せてきます。
（あるいは、もう押し寄せている。）
そしてその「定式化」の中心にあるものは、文字通り「式」なのです。
それは「解くための式」というより、まず「表現するための式」です。
ちなみに数式は英語で「Mathematical expression」、直訳すれば「数学的表現」となります。
現実問題のエッセンスを結晶化すること。
それが数式の持つパワーであり、実は数学が強烈に役立つ場面だったのです。

これは「ＯＲの４段階」として紹介されていた図です。-- 続･発想法（中公新書）より.
このように並べたとき、３つ目の「解く」は極端に言えばコンピュータが全部やってくれます。
電卓があれば筆算を行う必要はありませんが、それでも電卓のどのボタンを押すべきか、式の立て方だけは知っておく必要があります。
そうなると大事なのはむしろ「問題の定式化」「数式化」のステップなのですが、
どうも私(たち)は数学というものを「解く」ことを中心に考えるきらいがあるように思うのです。
数学とは、いかに解くか、いかにエレガントな解答を導き出すかであって、定式化、数式化のステップは、前座かオマケ程度。
たとえば学校で教わる数学の中で、文章題が占める割合はどの程度でしょうか。
たまたま私が目にした高校の教科書には、文章題はほとんどありませんでした。
ゼロかと思って尋ねてみたところ、「ここに１題あるよ」とのことだったので、１題だけ確認できました。
実際、小->中->高と進むにつれて、文章題は無くなる傾向にあります。
それだけ見ても、いかに「解く」以外がオマケ扱いか分かるでしょう。
（とってつけたような文章題が本当に「定式化」なのか、という疑問はひとまず置いておきましょう。）
それでも今後の実践を見据えるなら、いずれ「定式化」の方が「解く」以上のボトルネックになることでしょう。
そうなると「数学＝解く」のイメージがだいぶ変わってくるはずです。

イメージが変わると、何が変わるのか。
数学を必要とする人、使いこなせる人の範囲が変わります。
「解く数学」は、一握りの天才だけが必要とし、一握りの天才がいれば事足ります。
一方、「定式化の数学」は意思伝達ツールとしての性格が強く、チームメンバー全員が共有しないと意味がありません。
あるいは、共有できるような機械にＩＮＰＵＴしないと意味がありません。
また、天才だけでなく、凡人が使えないことには広がりがありません。
凡人で構わない、中身まで知る必要は無く、電卓のボタンが押せれば十分です。
ここはきれい事を並べるよりも、逆に、チームの中に１人だけ「定式化の数学」が通用しないメンバーが混じっている状況を想像してみて下さい。
その１人がどれだけ足を引っ張ることか。
特に、その１人が“無能な上司”だったりした場合には、悲惨なことになります。。。

さて、「式」が分析やシステム化に役立つのは、ある意味当然なのかもしれませんが、
これが意外な分野に役立つという話を最近耳にしました。
その意外な分野とは、「カウンセリング」です。
カウンセリングには「カウンセラーが自ら解決してはならない」という鉄則があるのだそうです。
では、カウンセラーは何をするのかというと、「ひたすら問題を整理して示す」だけです。
問題を解くのは、相談を持ちかけた本人でなければならない。
本人が解く力を身につけないことには、本当に解決したことにはならない、ということです。
新人カウンセラーがやりたくてウズウズするのだけれど、やってはいけないことは、指図すること。
つい口を突いて、ああしなさい、こうしなさいと言いたくなるのだけれど、それをグッと我慢するところが肝要なのです。
カウンセラーに相談に来る人は、ずばり解決策が聞きたくてやってくるのだけれど、
良いカウンセラーは決して直接的な解決方法を教えません。
（逆に言えば、「原因はずばり○○です」と言い切るカウンセラーは、あまり信頼できない。）
ただ、相談者がもってくる悩みを順序立てて整理し、明確な形で示すことに努める。
相談者が自ら解決できるような道筋を、ひたすらお膳立てするのだそうです。

このカウンセラーの話を聞いたとき、私は、これこそが定式化の威力だと思いました。
分析機器とコンピュータとカウンセリング。
この３つは全く別物に見えますが、定式化という側面からすれば、同じ心構えを有しています。
それは、「解く主体を全面的に信じてお任せする」ということ。
下手な自作や小細工を労するよりも、問題整理に全力を注ぎ、解くことはいっそ枯れた主体に一任する。
この定式化の方法こそが、システム化がとことん発展した現代に最もマッチしているように思えます。

量子力学序説 湯川秀樹（１９４７）

亡き父の書棚を整理していたら、この古い本が見つかった。

かの湯川先生の手になる著作なのだが、着目すべきはこの本が発行された時代である。
奥付を見ると、
　昭和二十二年二月一日初版印刷
　昭和二十二年二月十五日日初版發行
とある。

終戦後間もない“お腹を空かしていた”時代に、このような量子力学の本が出回っていたこと自体に驚く。
確か仁科研の逸話だったと思うのだが、食うや食わずの状況下で、
何の腹の足しにもならない“物理学研究”に固執する日本人の姿に、ＧＨＱはむしろ呆れたと言う。
それと同じ匂いが、この本から感じ取れる。
奥付には「湯川」の検印があり、何かとてもありがたい本のような気がしてくる。

不確定性原理が記述されたページ。「ガムマ線顕微鏡」の「思考實驗」というあたりがおもしろい。

序文を見ると、原稿が完成したのは「昭和十九年十月」とある。
その後「東京の印刷所の強制疎開で組版がこはされてしまつたので出版が非常に遅れ」、
「今回改めて京都の印刷所で組み始めることと」なって、やっと出たのがこの本である。
序文の最後には「昭和二十年十二月」とあるので、正に終戦を境に作られたのだと分かる。
つまり、湯川先生は少なくとも昭和十九年までは原稿を執筆し、
印刷所は終戦の最中にあって、何とかこの本の印刷にこぎ着けたわけだ。

本の中身を見ると、カタカナ表記が少ないことに気付く。
エネルギーは「勢力」であり、Plank や Einstein は原語表記となっている。
ただし「ベクトル」「オブザーバル」などはカタカナ表記なので、カタカナが全く無いわけでもない。
また、「波動力学」と「行列力学」の対比から、一般理論に向かうという章立てが為されている。
　第二章　波動力學
　第三章　行列力學の方法
　第四章　量子力学の基礎概念
　第五章　一般理論
今、「波動力学」とはあまり言わないと思うのだが、原点に返ると、これが素直な順序のように思う。
私は長らく「なぜシュレーディンガー方程式は行列なのか？」と疑問に思っていたのだが、この順番にたどると成立過程がよく分かる。

本には「定價80.00」とあるのだが、終戦直後の100円の価値はいったいどの位なのか。

　・公務員の初任給（月給）・・・540円
　・日雇い建設労働者日給（全国平均１人１日あたり）・・・７円５０銭
　・下宿料金（月額）・・・100円
　・食パン（１斤・450g）・・・１円２０銭
　　 -- 所場代300円　現在の貨幣価値では？昭和２１年当時の物価まとめ、より。
　　 >> http://locatv.com/beppin-300yen/

この数字から察するに、少なくとも数万円は下らない高価な本だったと分かる。
もし食パンに変えれば６６斤になったわけで、ＧＨＱが呆れる気持ちも分からなくはない。

当時貧乏学生であった父は、何を思って６６斤の食パンをがまんして、酔狂にもこの本を手にしたのだろうか。
当時の時代背景と父の年齢からして、この本の内容を深く理解していたとは到底思えない。
あるいは金額からして、父の父である祖父が本代を出したのかも知れない。
それにしても“食えない高額なもの”を買ってしまった、という事情には変わりない。
ここで、量子力学とは何なのかを思い起こすと、それが「新型爆弾」の基礎であったことに思い至る。
当時の日本は「新型爆弾」を落とされて、全く意気消沈していた時代である。
そこに、量子力学という本があった。
　「日本にも、こんなすごい学門がある。」
おそらくこれが、父がこの本から唯一確実に受け取ったメッセージであり、この本の真の価値なのではないか。

ちなみに、湯川秀樹がノーベル賞を受賞したのは1949年（昭和24年）。
なので、この本はノーベル賞の直前に発行されたものである。
そう考えると、実は二年間本屋にスタックされていたものを、
ノーベル賞のニュースに浮かれてミーハーな理由で購入したのかもしれない。

さて、現在この「量子力学序説」は刊行されているのかというと、
どうやら廃版となり、古本だけが残っている状況らしい。
さらに検索したところ、理系本の収集家である“とね”さんが同じ本を持っているとブログにしたためてあった。
* 量子力学序説（湯川秀樹著）：昭和２２年初版本
>> https://blog.goo.ne.jp/ktonegaw/e/bf5b874acf0b81d58d4bf8d8e66c6adf
今後、復刊されるかどうかは分からないので、興味ある方は今のうちに古本を探してみるとよいだろう。

運動エネルギー、指数分布、正規分布

[１]．なぜ運動エネルギーは速度の２乗なのか。
[２]．なぜエネルギーを無作為に分配すると、指数分布（ボルツマン分布）となるのか。
[３]．なぜ独立した試行を足し合わせると、正規分布となるのか。

一見何の関係も無さそうに見えるこの３つは、実は共通の思想から生み出されている。
３つ並べると、そこに見えてくるものがある。

[１]．なぜ運動エネルギーは速度の２乗なのか。

前提：
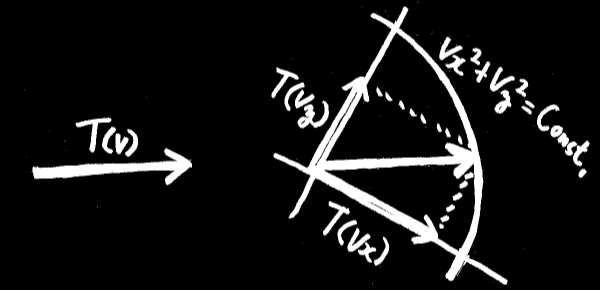
(1) 速度とはベクトル 〜 長さと向きを持った矢印で表される。
(2) 運動エネルギーとは、速度の向きに依存せず、大きさだけに依存するスカラー量（１個の数字で示される量）のことである。
(3) 空間とは一様に平ら（ユークリッド的）で、ベクトルは縦横に分解・合成できる。

とある速度ベクトルを別の角度から見ても、運動エネルギーは変わらない。
つまり、

この左右２つが等しくなければならない。
であれば、運動エネルギー T(v) = A v^2 以外にあり得ない。
　　※ なぜなら、ベクトルで円を描いた軌跡は vx^2 + vy^2 = r^2 = Const. だから。
　　※ また、求める関数は線形である必要がある。T(vx + vy) = T(vx) + T(vy).
　　※ この線形性から、求める関数は v２乗の１次式でなければならない。
この係数 A の半分のことを、我々は「質量」と呼んでいる。すなわち A = m/2 。
さらに、T(v) = (m/2) v^2 + C のように、ある一定の定数を付け加えても理論上は成り立つ。
通常、我々はこの定数の反対符合のことを「位置エネルギー」と呼んでいる。すなわち C = - U 。
位置エネルギー U は、一般的には場所ごとに異なる値を持っていてもかまわない。
つまり U は位置 q の関数 U(q) である。
　　※ あるいは空間の一様性を前提としたので(3)、場所ごとの違いを明示的に U(q) で示した、とも言える。

ここで「力」を「位置の違いによってエネルギー変化をもたらすベクトル」であると定義するならば、次のように書ける。

　F = ∂(T - U) /∂q
　　　(Tは運動エネルギー、Uは位置エネルギー、q は一般化座標)

力とは、運動エネルギー、位置エネルギーの別によらず「とにかくエネルギーの差分があるところに生じるベクトル」だと解釈できる。
実はここに、なぜ U にプラス符合ではなく、マイナス符合を付けたかの理由がある。
位置エネルギーが高くなるほど、坂を上るほど「反対の下り坂の向きに力を受ける」とするのが自然だから。

物体を動かす力の元になるエネルギー要因を、一定時間に渡って合計した値を「作用(action)」という。
力の元になるエネルギー要因 (T - U) は「ラグランジアン」と名付けられている。
ラグランジアンを用いて、作用 S は次のように書ける。

　S = ∫(T - U) dt

あらゆる物体は、作用を最も小さく（停留化）するように振る舞う。
これを「最小作用の原理」と言う。
最小作用の原理に、それ以上の「なぜ」は無い。
なぜかは説明できないけれど、原理として受け入れると全てが上手く行く。
実はたったこれだけで、古典力学の“全て”が構成できるのだ！
（詳しくは「ランダウ=リフシッツ理論物理学教程　力学」を参照のこと。）

[２]．なぜエネルギーを無作為に分配すると、指数分布（ボルツマン分布）となるのか。

前提：
(1) 確率の積の法則：
　　確率 Pa で生じる事象と、確率 Pb で生じる事象が、合わせて同時に起こる確率は Pa・Pb という確率の積になる。
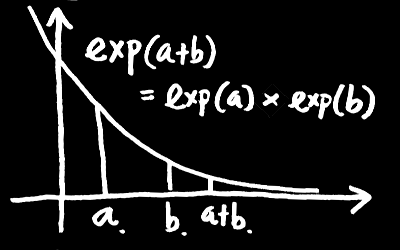
(2) 指数関数 exp(x) とは、足し算を掛け算に直す関数のことである。
　　　exp(a + b) = exp(a)・exp(b)
　　底の違いや定数倍を除いて、足し算を掛け算に直す（連続的で自然な）関数は指数関数だけである。

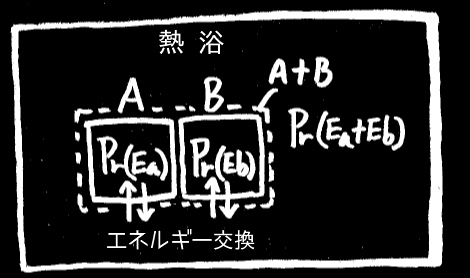
一定のエネルギーに満ちた（一定温度下にある）十分大きな熱浴環境を考える。
この環境の中で、熱浴とエネルギーをやり取りしている、とある一部分がエネルギー E を持つ確率分布 Pr を知りたい。
ある部分 A が、エネルギー Ea だけ持っている確率を Pr(Ea) としよう。
別の部分 B が、エネルギー Eb だけ持っている確率を Pr(Eb) としよう。
そして A と B には何ら特別な違いはなく、Pr はどの部分をとっても均質だったとしよう。
２つの部分を合わせた a+b 全体がエネルギー Ea+Eb を持つ確率は、確率の積の法則から、
　　Pr(Ea + Eb) = Pr(Ea)・Pr(Eb)。
これは、足し算を掛け算に直す関数なので、指数関数である。

もしこれが理想気体であったなら、個々の分子が持つ運動エネルギーの総和を
（さしあたり位置エネルギーは無視できるものとして）指数関数に従って分配すれば、
分子１個あたりが持つエネルギーの確率が導き出せる。
あらゆる化学反応は（レーザーか何かで局所的に特殊な分布でも作り出さない限り）、
このエネルギー分布に従って進行する。

あるいは、閉じた社会の中で均質な人々が一定量のお金を交換し合ったなら、
１人が持つお金の確率は（他に何の要因も無ければ）指数分布に従って分配されることになる。
（きっと社会における“化学反応”も、お金の分布に従って進行している。）

[３]．なぜ独立した試行を足し合わせると、正規分布となるのか。
　上記、[１] と [２] を合わせると、[３] が導き出される。

前提：
(1) 正規分布の骨格は、
　　N(x) = C exp( - A x^2 )

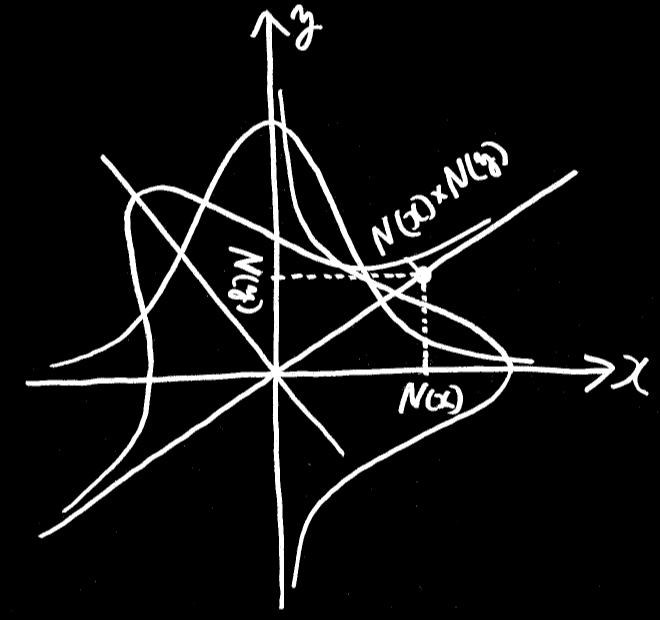
平面の的にボールを当てることを考えたとき、ボールが中心から外れる誤差の分布 N( r^2 ) の形状を知りたい。
誤差はあらゆる方向に対して独立なので、
　横方向 x の誤差は、N( x^2 )、
　縦方向 y の誤差は、N( y^2 )、
　縦横合わせた誤差は、N( x^2 )・N( y^2 )　　　<- 確率の積の法則.

的の中心からボールが当たった点までの距離の２乗は x^2 + y^2 だから、
　　N( x^2 + y^2 ) = N( x^2 )・N( y^2 )
これは、足し算を掛け算に直すのだから、指数関数である。
つまり、独立した誤差を合わせた確率分布は、
　　N(x) = exp( a x^2 )
の骨格を持つ。
係数 a がプラスでは成り立たない（発散する）ので、結局のところ正規分布は
　　N(x) = C exp( - A x^2 )
となる。
　 * 正規分布の導出 >> d:id:rikunora:20170310

正規分布が、あらゆる統計の基礎であることは言を俟たないであろう。

以上、３つの「なぜ」、力学、統計力学、統計学が、全て共通の思想から出ていることが読み取れただろうか。
あえて言葉で記すなら、
　『同一の実体を異なる視点から捉えれば、実体の普遍性から、視点を規定する法則が生じる』
とでも表現できようか。
　[１]．違う角度から見ても同一の実体がエネルギー。
　[２]．全体と部分で整合性がとれるのが、実現する確率分布。
　[３]．違う角度から見て、独立した試行の整合性がとれるのが、最も自然な確率分布。

あるいはネーターの定理に見る「対称性が保存則を導く」であるとか、
現代物理の基本要請である「ローレンツ不変」なども、同じ思想の所産だと思う。
これらについては徒に言葉をもてあそぶより、上記３つの核心にあるものを、じっくり鑑賞してほしい。