運動エネルギー、指数分布、正規分布
[1].なぜ運動エネルギーは速度の2乗なのか。
[2].なぜエネルギーを無作為に分配すると、指数分布(ボルツマン分布)となるのか。
[3].なぜ独立した試行を足し合わせると、正規分布となるのか。
一見何の関係も無さそうに見えるこの3つは、実は共通の思想から生み出されている。
3つ並べると、そこに見えてくるものがある。
[1].なぜ運動エネルギーは速度の2乗なのか。
前提:
(1) 速度とはベクトル 〜 長さと向きを持った矢印で表される。
(2) 運動エネルギーとは、速度の向きに依存せず、大きさだけに依存するスカラー量(1個の数字で示される量)のことである。
(3) 空間とは一様に平ら(ユークリッド的)で、ベクトルは縦横に分解・合成できる。
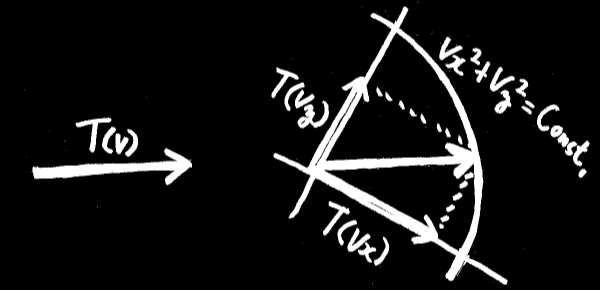
とある速度ベクトルを別の角度から見ても、運動エネルギーは変わらない。
つまり、
この左右2つが等しくなければならない。
であれば、運動エネルギー T(v) = A v^2 以外にあり得ない。
※ なぜなら、ベクトルで円を描いた軌跡は vx^2 + vy^2 = r^2 = Const. だから。
※ また、求める関数は線形である必要がある。T(vx + vy) = T(vx) + T(vy).
※ この線形性から、求める関数は v2乗の1次式でなければならない。
この係数 A の半分のことを、我々は「質量」と呼んでいる。すなわち A = m/2 。
さらに、T(v) = (m/2) v^2 + C のように、ある一定の定数を付け加えても理論上は成り立つ。
通常、我々はこの定数の反対符合のことを「位置エネルギー」と呼んでいる。すなわち C = - U 。
位置エネルギー U は、一般的には場所ごとに異なる値を持っていてもかまわない。
つまり U は位置 q の関数 U(q) である。
※ あるいは空間の一様性を前提としたので(3)、場所ごとの違いを明示的に U(q) で示した、とも言える。
ここで「力」を「位置の違いによってエネルギー変化をもたらすベクトル」であると定義するならば、次のように書ける。
F = ∂(T - U) /∂q
(Tは運動エネルギー、Uは位置エネルギー、q は一般化座標)
力とは、運動エネルギー、位置エネルギーの別によらず「とにかくエネルギーの差分があるところに生じるベクトル」だと解釈できる。
実はここに、なぜ U にプラス符合ではなく、マイナス符合を付けたかの理由がある。
位置エネルギーが高くなるほど、坂を上るほど「反対の下り坂の向きに力を受ける」とするのが自然だから。
物体を動かす力の元になるエネルギー要因を、一定時間に渡って合計した値を「作用(action)」という。
力の元になるエネルギー要因 (T - U) は「ラグランジアン」と名付けられている。
ラグランジアンを用いて、作用 S は次のように書ける。
S = ∫(T - U) dt
あらゆる物体は、作用を最も小さく(停留化)するように振る舞う。
これを「最小作用の原理」と言う。
最小作用の原理に、それ以上の「なぜ」は無い。
なぜかは説明できないけれど、原理として受け入れると全てが上手く行く。
実はたったこれだけで、古典力学の“全て”が構成できるのだ!
(詳しくは「ランダウ=リフシッツ理論物理学教程 力学」を参照のこと。)
[2].なぜエネルギーを無作為に分配すると、指数分布(ボルツマン分布)となるのか。
前提:
(1) 確率の積の法則:
確率 Pa で生じる事象と、確率 Pb で生じる事象が、合わせて同時に起こる確率は Pa・Pb という確率の積になる。
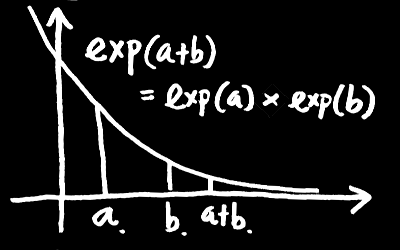
(2) 指数関数 exp(x) とは、足し算を掛け算に直す関数のことである。
exp(a + b) = exp(a)・exp(b)
底の違いや定数倍を除いて、足し算を掛け算に直す(連続的で自然な)関数は指数関数だけである。
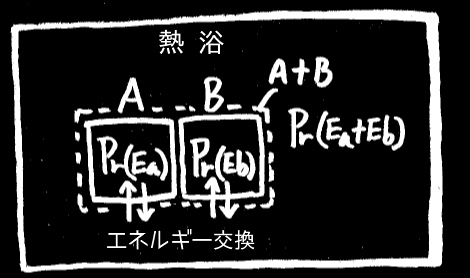
一定のエネルギーに満ちた(一定温度下にある)十分大きな熱浴環境を考える。
この環境の中で、熱浴とエネルギーをやり取りしている、とある一部分がエネルギー E を持つ確率分布 Pr を知りたい。
ある部分 A が、エネルギー Ea だけ持っている確率を Pr(Ea) としよう。
別の部分 B が、エネルギー Eb だけ持っている確率を Pr(Eb) としよう。
そして A と B には何ら特別な違いはなく、Pr はどの部分をとっても均質だったとしよう。
2つの部分を合わせた a+b 全体がエネルギー Ea+Eb を持つ確率は、確率の積の法則から、
Pr(Ea + Eb) = Pr(Ea)・Pr(Eb)。
これは、足し算を掛け算に直す関数なので、指数関数である。
もしこれが理想気体であったなら、個々の分子が持つ運動エネルギーの総和を
(さしあたり位置エネルギーは無視できるものとして)指数関数に従って分配すれば、
分子1個あたりが持つエネルギーの確率が導き出せる。
あらゆる化学反応は(レーザーか何かで局所的に特殊な分布でも作り出さない限り)、
このエネルギー分布に従って進行する。
あるいは、閉じた社会の中で均質な人々が一定量のお金を交換し合ったなら、
1人が持つお金の確率は(他に何の要因も無ければ)指数分布に従って分配されることになる。
(きっと社会における“化学反応”も、お金の分布に従って進行している。)
[3].なぜ独立した試行を足し合わせると、正規分布となるのか。
上記、[1] と [2] を合わせると、[3] が導き出される。
前提:
(1) 正規分布の骨格は、
N(x) = C exp( - A x^2 )
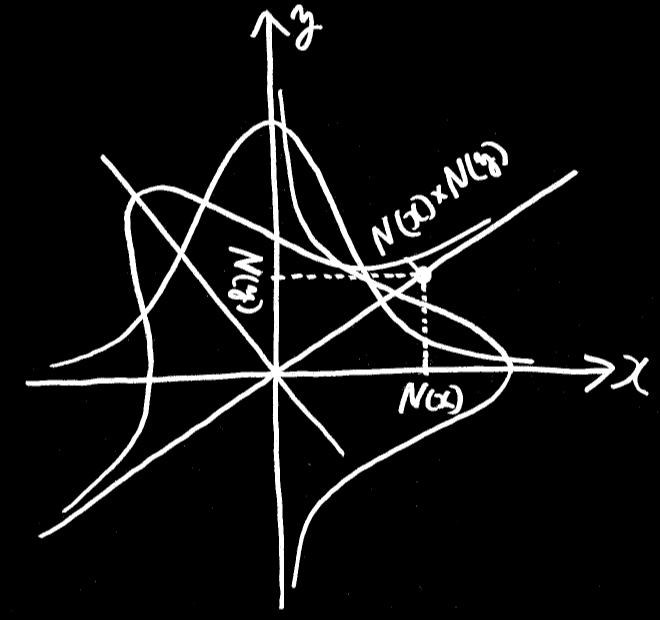
平面の的にボールを当てることを考えたとき、ボールが中心から外れる誤差の分布 N( r^2 ) の形状を知りたい。
誤差はあらゆる方向に対して独立なので、
横方向 x の誤差は、N( x^2 )、
縦方向 y の誤差は、N( y^2 )、
縦横合わせた誤差は、N( x^2 )・N( y^2 ) <- 確率の積の法則.
的の中心からボールが当たった点までの距離の2乗は x^2 + y^2 だから、
N( x^2 + y^2 ) = N( x^2 )・N( y^2 )
これは、足し算を掛け算に直すのだから、指数関数である。
つまり、独立した誤差を合わせた確率分布は、
N(x) = exp( a x^2 )
の骨格を持つ。
係数 a がプラスでは成り立たない(発散する)ので、結局のところ正規分布は
N(x) = C exp( - A x^2 )
となる。
* 正規分布の導出 >> d:id:rikunora:20170310
正規分布が、あらゆる統計の基礎であることは言を俟たないであろう。
以上、3つの「なぜ」、力学、統計力学、統計学が、全て共通の思想から出ていることが読み取れただろうか。
あえて言葉で記すなら、
『同一の実体を異なる視点から捉えれば、実体の普遍性から、視点を規定する法則が生じる』
とでも表現できようか。
[1].違う角度から見ても同一の実体がエネルギー。
[2].全体と部分で整合性がとれるのが、実現する確率分布。
[3].違う角度から見て、独立した試行の整合性がとれるのが、最も自然な確率分布。
あるいはネーターの定理に見る「対称性が保存則を導く」であるとか、
現代物理の基本要請である「ローレンツ不変」なども、同じ思想の所産だと思う。
これらについては徒に言葉をもてあそぶより、上記3つの核心にあるものを、じっくり鑑賞してほしい。