平均と分散の物理モデル

以下は、前エントリー「なぜ分散は２乗の和なのか」d:id:rikunora:20190409 から出たオマケの与太話。

なぜ分散は２乗なのか、と問われたとき、「分散を最も小さくする点が平均値だから」というのが１つの答でした。
この答を物理的なモデルに当てはめると、こんな絵が描けます。

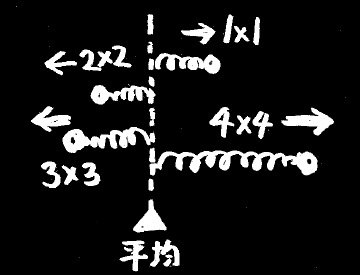
・各データと、とある１点をバネで結んだとき、１点は平均点で止まる。

このモデルで分散は、「バネに溜まったエネルギー」に対応付けられます。
分散が足し算できること（加法性）は、「エネルギー保存則」として理解できます。

ところが分散は、こんな物理モデルに当てはめることもできます。

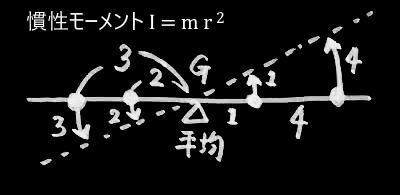
・各データに重みを付けてバランスをとったとき、重心は平均点と一致する。

このモデルの場合、分散は「慣性モーメント」に対応付けられます。
分散が足し算できること（加法性）は、「角運動量保存則」として理解できます。

以下、確率・統計入門（小針あき宏）という本からの引用。

これだけを見ていると何でもないようだが、これは‘平均の持つ意味’についての、一つの思想を物語っている。
・・・平均値をその分布の代表とする理由は、そのまわりの分散が最小ということによって特徴づけられているわけである。
ρ(x)を質量密度と考えると、分散は慣性能率に対応していることは、説明を待たないであろう。
そして自由な剛体の運動は、加えられた力をＦ，質量をＭとするとき、
　　　Ｆ＝Ｍｘ''
によって記述される、重心の曲線運動と、
慣性能率をＩ，重心からの力の加えられたところまでの距離をｒとすると
　　　Ｆｒ＝Ｉθ''
によって記述される、重心回りの回転運動によって完全に決定されるが、
どうして《重心のまわり》に回転がおこるか、というと、そのまわりの慣性能率が最小だから、に他ならない。
そして重心～平均、慣性能率～分散、の対応を見るとき、平均の持つ意味について、新たな理解が生ずるだろう。

エネルギーとは、「物理的に、時間変化に対して不変な保存量」のことです。
角運動量とは、「物理的に、角度の変化に対して不変な保存量」のことです。
物理学には“ネーターの定理”と名付けられた定理があります。
標語的に言うと、「対称性あるところに保存則がある」といった主張です。
ネーターの定理によると、
　・時間並進の対称性から「エネルギー保存則」が、
　・回転の対称性から「角運動量保存則」が、
　・空間並進の対称性から「運動量保存則」が、
それぞれ導かれます。

ならば、分散を「運動量保存則」に結びつけるような物理モデルは無いものだろうか・・・
少し考えてみたのですが、うまいモデルは思いつきませんでした。
それもそのはず、エネルギーと角運動量が２次式なのに対し、運動量保存則は１次式なので、土台あてはまらないのです。
※ 運動量保存則は、”分散”ではなく”平均”に結びつけられます。
※ 平均は、確かに平衡移動について対称、一斉にゲタを履かせても不変ですが、あまりにもアタリマエなので意識されません。

話はこれだけなのですが、以上は何も分散だけに限った話ではなく、２次式で表されるような量全般に言えるように思えます。
もともと２次式に当てはまるような量であれば何であれ、
エネルギーや角運動量に関連付いたもっともらしい物理モデルとして表される、ということです。
一般に、理解の仕方や解釈は、個々人の感性やセンス、才能といったものに委ねられると言われがちです。
しかし、この分散の物理モデルを見て思うことは、
「思考の筋道とは全くの自由奔放ではなくて、自ずと規定されている」ということです。
不自然さを感じさせない発想は、文字通り“物の理”に叶っているのです。
そうした“物の理”に叶った発想だけが、分かりやすく、人に伝えやすく、結果的に生き残るのではないか。
そんな風に思えるのです。

確率・統計入門