サイコロの和と多次元立方体の関係

複数個の一様分布の和は、厳密にはどのような分布に従うのか。

２個のサイコロを同時に振ったとき、最も出やすいのは合計が７のとき。
なぜなら、1+6, 2+5, 3+4, 4+3, 5+2, 6+1 と、６通りの出方があるからです。
それに比べて合計が２となるのは、1+1 の１通り。合計が１２となるのは 6+6 の１通りしかありません。
グラフにすれば、このようなテント型になります。

同じようにして、３個のサイコロの和をグラフにまとめると、こんな形になります。

* 計算サイト・サイコロの和の確率
>> http://www.calc-site.com/probabilities/dice_total

さらにサイコロの数を１０個、２０個と増やしていくと、グラフは滑らかな釣り鐘型曲線へと近づきます。
この釣り鐘型のカーブが「正規分布」なのだ、という話は統計学の教科書に譲るとして、
ここで問題にしたいのは正規分布に至るまでの途中の段階です。
たとえば上のサイコロが３個 ～ 一様分布を３個足し合わせた結果は、厳密にはどのようなカーブなのでしょうか。
あるいは一様分布を７個足し合わせた結果は、正確にはどのような分布なのでしょうか。

先に結果を示します。
以下は、Mathematicaというソフトで一様分布を１～７個まで足し合わせた結果を描いたものです。
（※ただしグラフの高さは正規化されていません。）

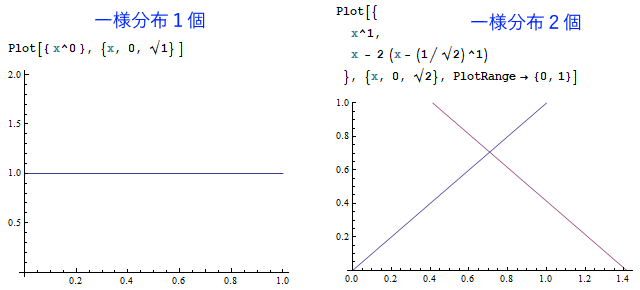
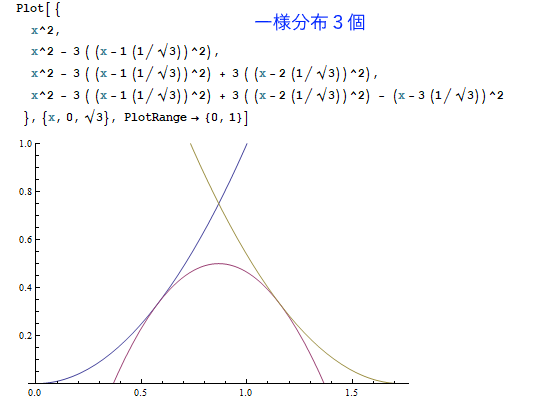
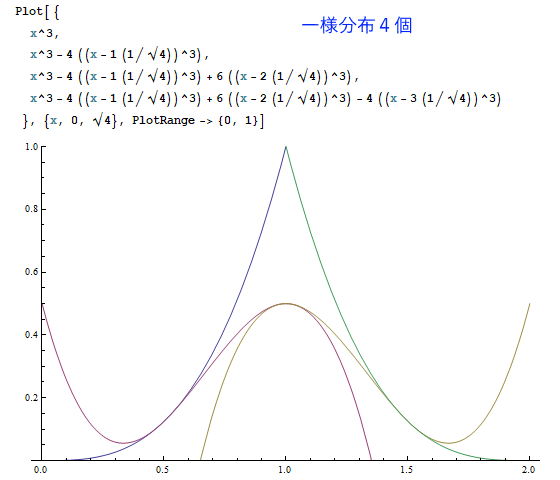
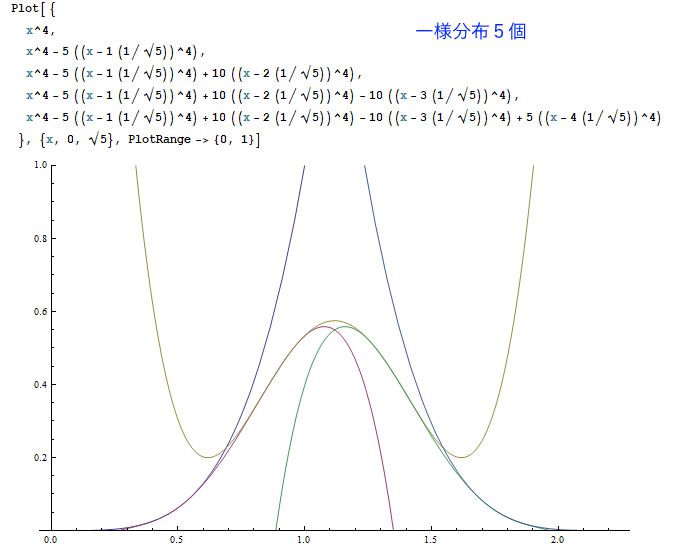
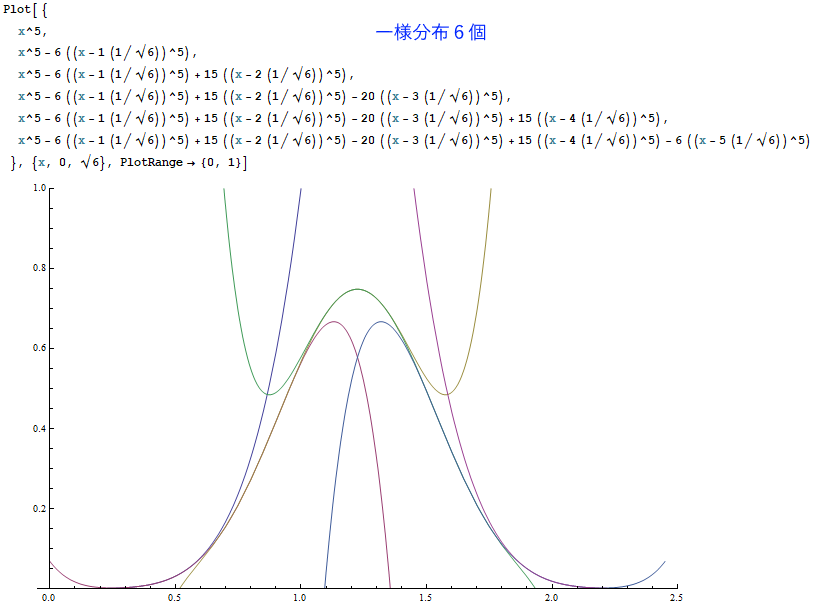
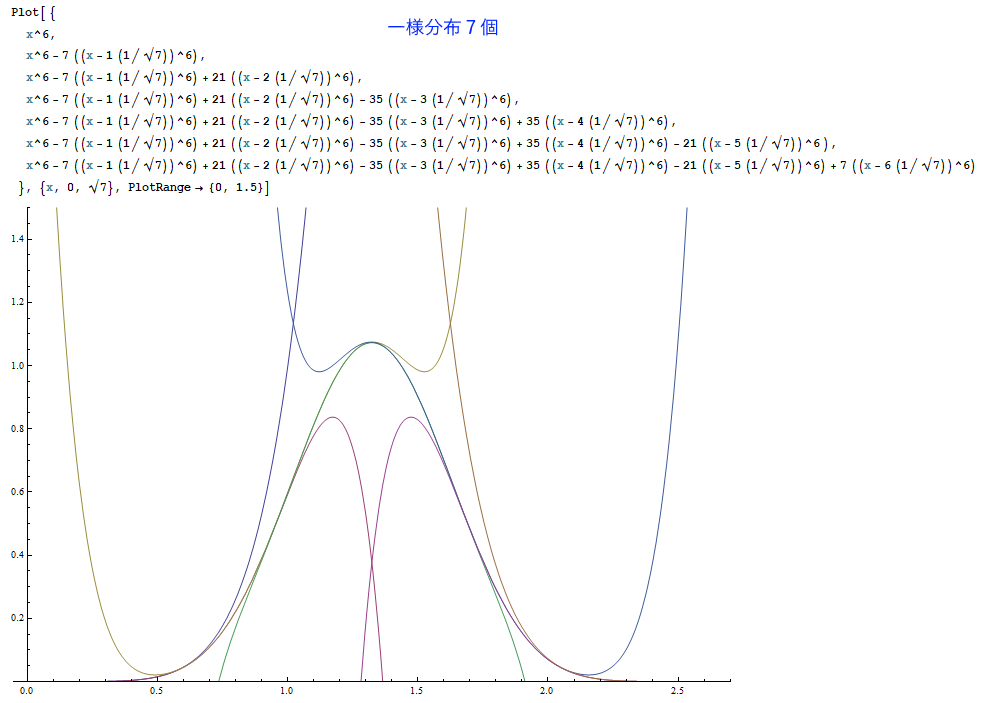
一定の美しい規則に従って、釣り鐘型曲線が削り出される様子が見て取れたでしょうか。
Ｎ個の一様分布の和は、Ｎ本の（Ｎ－１）次曲線の組み合わせから成り立ちます。
たとえばＮ＝３（サイコロ３個）の場合、次の３本の２次曲線で、３つの区間をカバーしています。

　y = x^2　　　-- {x = 0～√3/3 の区間}
　y = x^2 - 3 ( (x-1(1/√3))^2 )　　　-- {x = √3/3～2√3/3 の区間}
　y = x^2 - 3 ( (x-1(1/√3))^2 ) + 3 ( (x-2(1/√3))^2 )　　　-- {x = 2√3/3～√3 の区間}

では、どうやってこれらの曲線を求めたのか。
実はこれらの曲線は、Ｎ次元の立方体を、対角線に直行して切った切断面の面積のグラフなのです。
まず２個のサイコロで考えてみましょう。

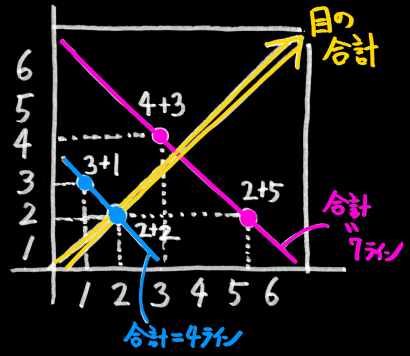
１個目のサイコロの目を横軸に、２個目のサイコロを縦軸に、全ての出目を図示すると６×６の正方形となります。
この正方形の上で、２つの目の合計が一定となる線は、右下がり45度の直線となります。
たとえば、上の図で青で引いた線は合計が４となる直線。
赤で引いた線は合計が７となる直線です。
そして、これらの合計が一定となる直線の長さは、その合計値が出る場合の数＝確率に比例しています。
そこで、改めて正方形の黄色い対角線を横軸にして見れば（つまり図を45度傾けて見れば）、
正方形がそのままテント型の分布を形作っていることに気付きます。

次に次元を１つ上げて、３個のサイコロの和を考えてみましょう。

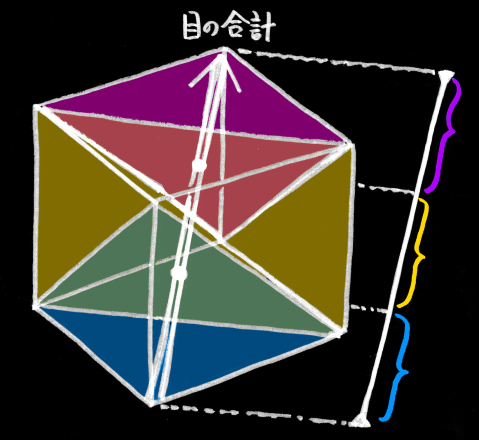
３個のサイコロを３次元の縦、横、高さに配置すれば、６×６×６の立方体となります。
この立方体の上で、３つの目の合計が一定となる面は、立方体の対角線に直行する面となります。
立方体の対角線を軸にして、切断面の面積をグラフに描けば、３個のサイコロ（一様分布）の和の分布となります。
立方体の切断面は、図の手前から順に３つのパートに分かれます。
１番手前の青色のパートは、１つの頂点からスタートし、三角錐がどんどん大きくなる過程。
２番目の中間にある黄色のパートは、断面の正三角形から、もう一方の反対向きの正三角形に向けて、６角形の断面が徐々に変形する過程。
３番目の赤色のパートは、１番目と反対に三角錐がどんどん小さくなる過程です。
１番目と３番目のパートが２次曲線となることは、断面積が辺の長さの２乗となることから想像が付くでしょう。
ちょっと悩むのは２番目の、中間にある６角形断面のパートです。

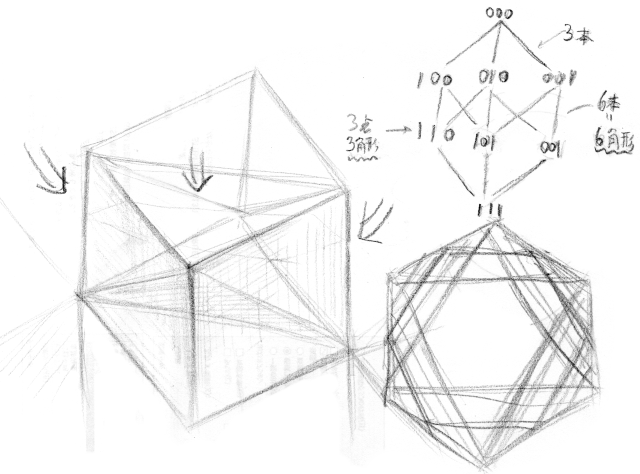
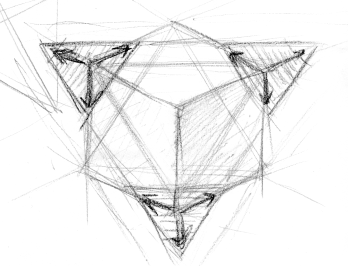
この２枚のスケッチは、６角形断面のパートを取り出して描いたものです。
特に２枚目のスケッチをよく見てください。
断面の６角形とは、拡大する１つの正三角形の３つの頂点から、３つの正三角形を差し引いた残りだと見なせます。
拡大する１つの正三角形と、差し引く３つの正三角形は、実は全く同じ図形を空間的にずらしたものです。
というのも、差し引く３つの正三角形は、元の立方体の隣に位置する、同じ形の立方体の断面だからです。
空間を埋め尽くしている立方体の群れを切断することを想像すれば、
とある１つの立方体の断面積は、同じ形の正三角形を足したり引いたりすることで算出できるのです。
より具体的に、６角形断面の中間パートは次のように定式化できます。

　(１番目のパートの正三角形) - ３×(途中から始まった２番目のパートの正三角形）

立方体の対角線の長さは √3 です。
そして、対角線に対する３つのパートの幅はそれぞれ等しく √3/3 ずつです。
なので (途中から始まった…）とは、数字の上では √3/3 だけずらすことを意味します。
以上に基づいて式を完成させたものが、当初に挙げた「一様分布３個」のグラフだったのです。

※３個のサイコロについては、以下がわかりやすいです。
※『ちょっとした「つり鐘型曲線」を描いてみる』
※ https://teenaka.at.webry.info/201704/article_12.html
※『ちょっとした「つり鐘型曲線」と正規分布の関係』
※ https://teenaka.at.webry.info/201704/article_13.html

４個のサイコロ（一様分布）の足し合わせは、４次元立方体を対角線に直行するように切断した断面として表わされます。

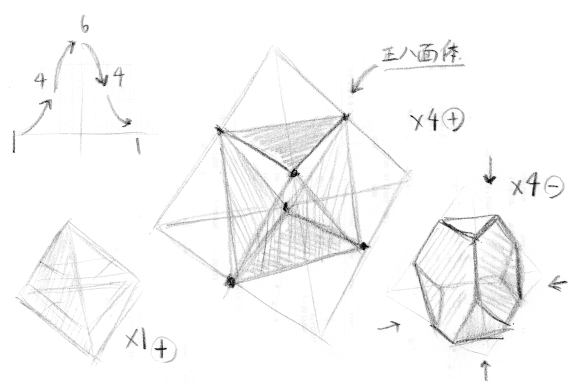
４次元立方体を直接描くことはできませんが、断面である３次元図形を想像することは可能です。
４次元立方体の断面は、以下の４つのパートから成り立ちます。

　第１パート：正４面体がだんだん大きくなる過程。
　第２パート：正４面体の各頂点が削れ、正８面体となる過程。
　第３パート：正８面体の４つの面が成長して、正４面体となる過程。
　第４パート：正４面体がだんだん小さくなる過程。

これらの過程は、３次元の場合と同じように、最初の正４面体の足し引きによって定式化できます。

　第１パート：(正４面体)
　第２パート：(正４面体) - ４×(１つずらした正４面体)
　第３パート：(正４面体) - ４×(１つずらした正４面体) + ６×(２つずらした正４面体)
　第３パート：(正４面体) - ４×(１つずらした正４面体) + ６×(２つずらした正４面体) - ４×(３つずらした正４面体)

式中に登場する正四面体の数、４、６、４ は、二項係数となっています。
二項係数とは、ｎ個の中からｋ個の要素を取り出す組み合わせの数のことです。
なぜ二項係数となるのか。
４次元立方体の各頂点に、４桁の０または１で番号を付けることを考えます。
４つの頂点は４つの次元に対して、それぞれ手前と奥のどちらか（あるいは上下、右左などの）一方に位置付けられます。
最も手前にある頂点 0000 から出発して、1111に向かって辺で結ばれた頂点を線で結んでたどってゆくと、以下のような図形が描かれます。

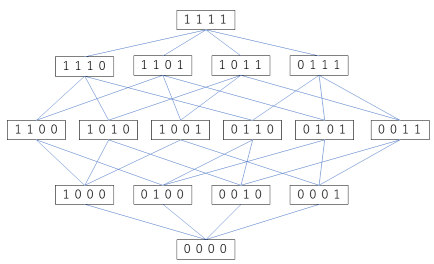
（このような図を“ハッセ図”と言います。）
この図から、同一切断面に並ぶ頂点の数は「４つの桁の中に何個かの１が入る組み合わせの数」になっていることが分かります。
そしてこの頂点の数は、そのまま足し引きすべき図形（正四面体）の数となっているわけです。

以上で見てきた関係は、そのまま次元数が上がっても変わりません。

・最初のパートはＮ次元の角錐から始まる。グラフの上で、最初の区画は(Ｎ－１)次の曲線となる。
・最初のパートの図形（Ｎ次元の角錐）を、二項係数に従って足し引することによって、２番目以降のパートをつなげる。
　（足し引きは、プラスマイナスを交互に繰り返せばよい。）

こうして、Ｎ次元立方体の断面から、Ｎ個の一様分布の和が描き出されます。
※ 最初のパートとなるＮ次元の角錐の体積は、前の記事に記載しました >> d:id:rikunora:20190210

サイコロの数をうんと増やした極限が正規分布になる、ということは、正規分布とは“無限次元立方体の切断面”の形だということになります。
単なるサイコロの足し合わせを、多次元立方体の切断面として捉えるならば、また違った風景が見えてくる。