コーシー分布とarctan微分
目隠しをしたアーチェリー選手が、長い壁に向かってランダムにたくさんの矢を放ったら、矢の当たった点はどのような分布に従うか。
答は「コーシー分布」(Cauchy distribution) になります。
コーシー分布は、よく知られている正規分布とは、似たようなベル型カーブであってもかなり性質が異なります。
特に際だった性質は、“平均も分散も無い”ということ。
たとえ1本であっても、うんと遠くに矢が当たったなら、それに引っ張られて平均が安定しないということです。
* そんなの常識、あたりまえでない大数の法則 >> http://miku.motion.ne.jp/stories/08_LargeNum.html
この図から、コーシー分布がどんな数式で表されるか、考えてみましょう。
矢の角度θを動かしたとき、矢のあたる場所は tan(θ) となります(定数は省略)。
矢の当たった数、つまり当たった点の密度は、tan(θ) のグラフの曲線の変化が大きいところほど濃くなります。
tan(θ) のグラフの曲線を横から見たものは tanの逆関数 arctan(θ) ですから、
当たった点の密度は arctan(θ) の変化、すなわち arctan(θ) の微分ということになります。
arctan の微分はどうなるか。
WolframAlpha (https://www.wolframalpha.com/) という計算サイトに行って、
「arctan(x)'」と入力すると、以下の答が得られます。
(d/dx) arctan(x) = 1 / (x^2 + 1) ・・・これがコーシー分布の実質的な骨格です。
この arctanの微分の意味を、アーチェリーから問い直してみましょう。
まず、矢の代わりにサーチライトで長い壁を照らすことを考えます。
壁の正面を照らしたとき、サーチライトのスポットの大きさが1だったとましょう。
正面から x だけ離れた位置をサーチライトで照らしたなら、スポットの大きさはピタゴラスの定理から √(x^2+1)だけ大きくなります。
今考えたサーチライトでは、距離が x だけ離れた様子を想定しましたが、
アーチェリーの場合は距離ではなく、角度が変動の元になっていました。
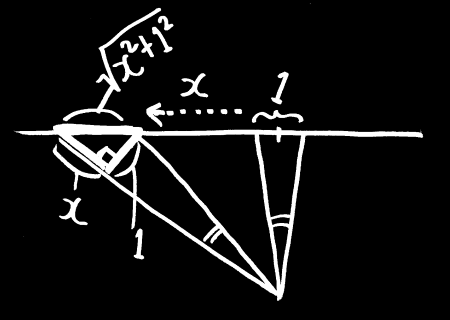
この距離と角度の関係を表したのが次の図です。
ある一定の角度が、正面の長さの1に対応していたとき、
x だけ離れた場所で対応する長さは、やはりピタゴラスの定理から √(x^2+1)となります。
コーシー分布=「角度の変化に対する、矢が当たった点の密度の変化」は、上記、
1.サーチライトのスポットの大きさ -- 密度そのものの変化
2.長さと角度の対応関係
の2つを掛け合わせた値に反比例するので、結局
コーシー分布 = 1 / { √(x^2+1) * √(x^2+1) } = 1 / (x^2+1)
となります。
なぜ反比例なのかというと、スポットが長くなればなるほど、密度は薄くなるから。
「目隠しされたアーチェリー選手」のたとえは、「禁断の市場(マンデルブロ著)」という本から引用したものです。
マンデルブロは、市場の変動は正規分布のように安定したものではなく、
むしろコーシー分布に近い“平均も分散も無い”世界なのだと主張しています。

- 作者: ベノワ・B・マンデルブロ,リチャード・L・ハドソン,高安秀樹,雨宮絵理,高安美佐子,冨永義治,山崎和子
- 出版社/メーカー: 東洋経済新報社
- 発売日: 2008/06/06
- メディア: 単行本
- 購入: 9人 クリック: 91回
- この商品を含むブログ (32件) を見る
ところで、正規分布とはどのようなものであったかと言うと、
「平面の的を目がけてボールを当てたとき、中心からのずれの大きさの分布」
ということでした。
* 正規分布の導出 >> [id:rikunora:20170310]
ということは、ボールだと正規分布で、矢だとコーシー分布なのか?
両者の違いは、ボールは距離(長さ)で測っているが、矢は角度で測っている、という点にあります。
正規分布の“長さ”で行っていた議論を、そっくりそのまま“角度”に置き換えようとしても、うまく行きません。
的の中心から、横方向に長さ x、縦方向に長さ y ずれた点にボールが当たる確率は x^2+y^2 と表せるのですが、
横方向に角度 θ、縦方向に角度 φ ずれた点に矢が当たる確率は、θとφの何らかの和にはなりません。
2つの分布の違いは結局のところ、測り方の違いに求められると思うのです。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
久々にブログ更新しました。
ここ最近雑事が多く、ブログを書くゆとりがありません。
頂いたコメントなど、ろくに返事もできず、すいません。