正規分布以外の区間推定

ｔ分布を用いた平均値の区間推定には、「正規母集団を仮定する」というただし書きが付いています。
ということは、母集団が正規分布でなかった場合、区間推定は使えないのでしょうか。
母集団の分布は未知であることが多いので、もし正規母集団という条件が絶対だったなら、
区間推定は実際の現場ではほとんど使えない理屈ということになってしまいます。

結論から言えば、たとえ母集団が正規分布で無くても、
母集団から抜き出した標本の平均値が正規分布に従うなら、区間推定の方法を使うことができます。
中心極限定理によれば、ほとんどの分布は（コーシー分布やべき分布といった“平均の無い”分布を除けば）
標本の平均が正規分布に近づくので、区間推定は正規母集団以外にも広く適用可能なのです。
ただし、正規分布から外れるほど大きなサンプルサイズ（データの数）が必要です。
目安は以下の通りです。
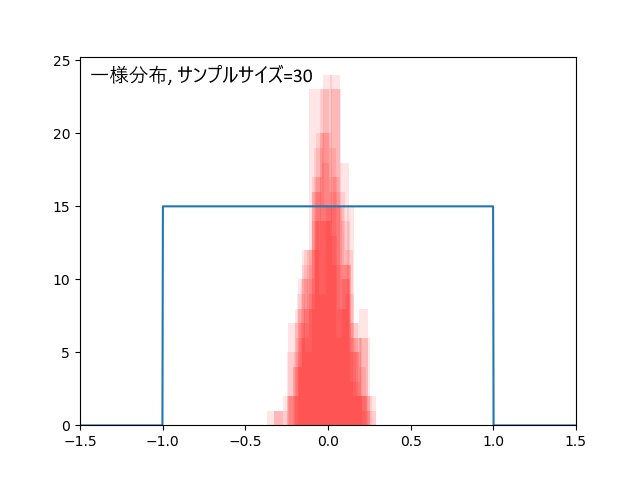
　・一様分布なら３０個以上
　・ベータ分布(a=4,b=2)くらい歪んだ分布なら１００個以上
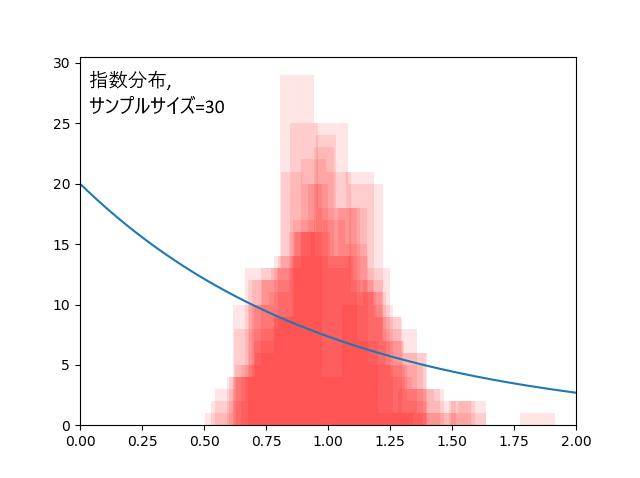
　・指数分布のように一方的に偏った分布なら３００個以上

これらの目安はどうやって得られたのかというと、ひたすらシミュレーションを繰り返した結果です。
以下に掲げる図は、正規分布以外の特定の分布から、何度も繰り返しサンプルを抜き出して区間推定を行った結果です。
図に示す曲線が元になった母集団の分布。
赤でぼんやり描かれているのは、標本を抜き出す操作を１００回繰り返したときの、標本平均のヒストグラムです。
１００回の繰り返しを１０セット行い、ヒストグラムは１０枚重ねて描いてあります。

●正規分布


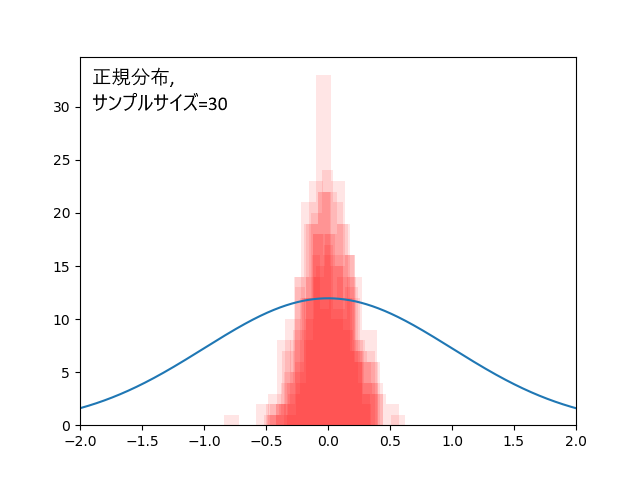
まずこれが正規分布、サンプルサイズ３０個の場合。
95%信頼区間であれば、100回のうち95回は真の平均値が信頼区間の中に含まれます。逆に言えば、5回は外れます。
データ30個の場合、外れ回数は5.2回。標本平均の標準偏差=0.18。

●一様分布

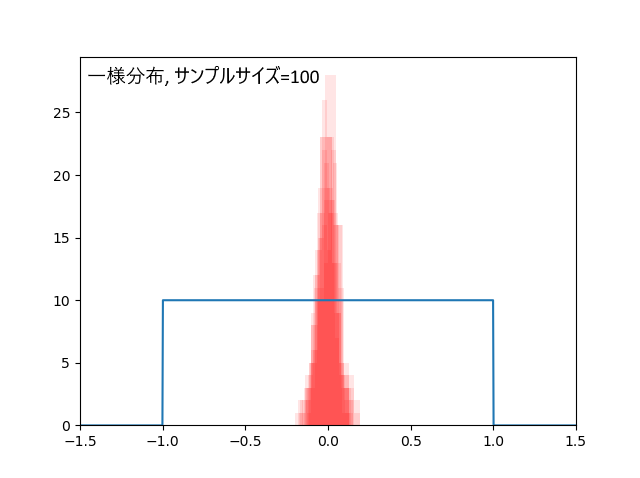
一様分布、データ30個の場合と、100個の場合。
データ数が増えるほど平均値の推定幅が小さくなる様子が見てとれます。
データ30個の場合、外れ回数は4.5回。標本平均の標準偏差=0.10。
データ100個の場合、外れ回数は5.2回。標本平均の標準偏差=0.06。
データ数30個であっても区間推定は十分有用でした。

●ベータ分布(4,2)

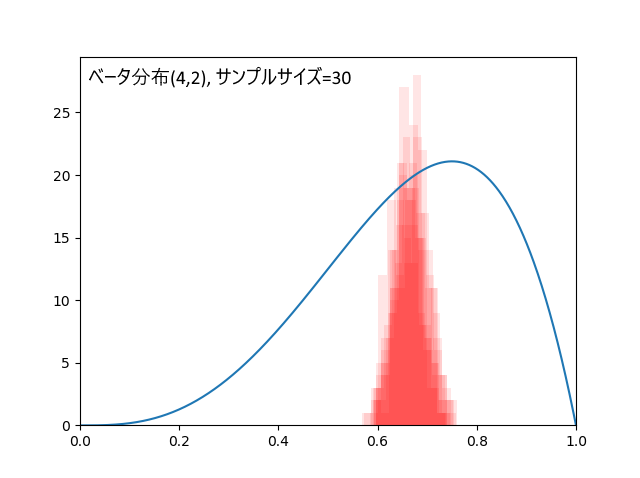
ベータ分布(4,2)、真の平均値は0.666...、歪んだ分布の例として取り上げました。
データ30個の場合、外れ回数は4.2回。標本平均の標準偏差=0.031。
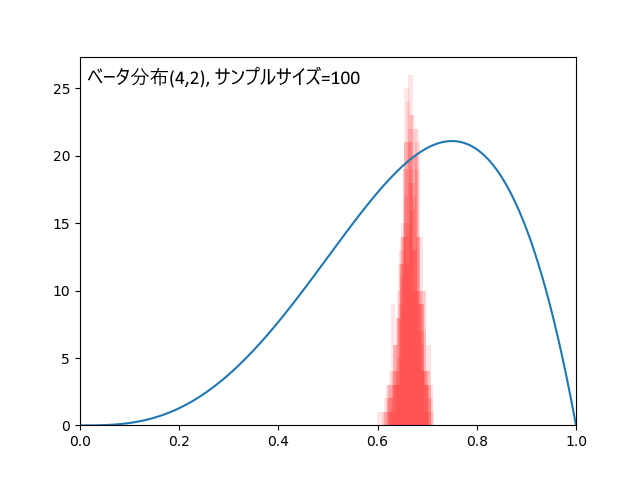
データ100個の場合、外れ回数は5.5回。標本平均の標準偏差=0.018。
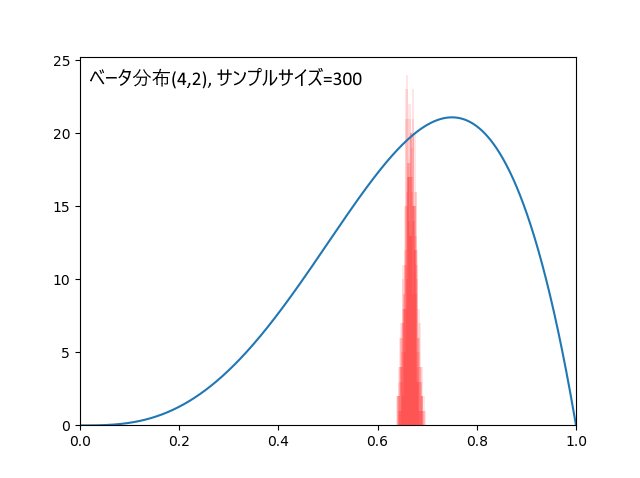
データ300個の場合、外れ回数は4.9回。標本平均の標準偏差=0.010。
30個だと結果が不安定（ばらつきが大きい）でしたが、100個あればかなり安定します。

●指数分布

指数分布、真の平均値は1。
データ30個の場合、外れ回数は8.7回。標本平均の標準偏差=0.18。
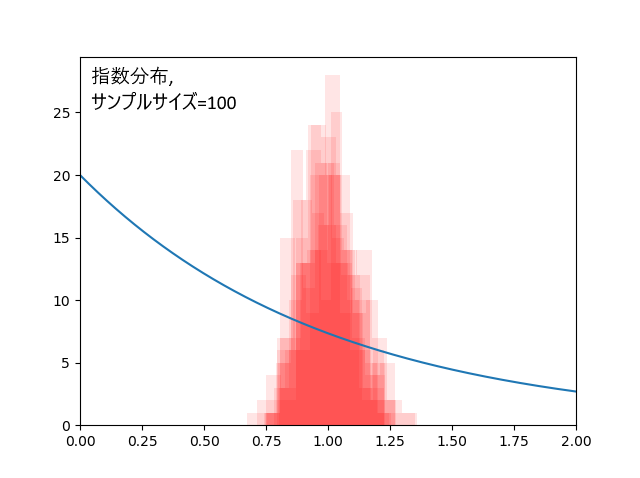
データ100個の場合、外れ回数は6.6回。標本平均の標準偏差=0.10。
データ300個の場合、外れ回数は5.3回。標本平均の標準偏差=0.06。
元の分布がここまで偏っていたなら、安定した結果には300個のデータが欲しいところです。

●コーシー分布

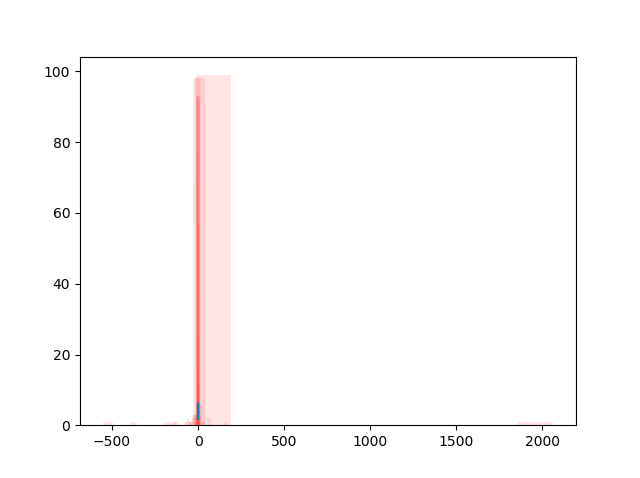
コーシー分布には“平均値がありません”。なので、区間推定は使えません。
上はデータ30個の場合ですが、確かに見ての通り、区間推定は適用できません。
* コーシー分布とarctan微分 >> [id:rikunora:20171210]

検索したところ、ここに詳しく書かれていました。
* 大人の知らない統計学 ６　　非正規分布の信頼区間
>> https://blogs.yahoo.co.jp/pironotakarabako/63655916.html

以下にシミュレーションのソースを示します。
（分布や数値の付け替えはコメントで行っています。わかりずらい。）
シミュレーションといっても、要は区間推定をひたすら繰り返しているだけです。

# -*- coding: utf-8 -*-
"""
区間推定の頑健性、正規母集団以外では、どれほどサンプルがあれば妥当なのか。
"""
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

class IntervalCheck:

    N_TRIAL_SET =  10   # 試行セット回数
    N_TRIAL     = 100   # 試行回数
    N_SAMPLE    = 30    # 100   # 300   # サンプルサイズ＝データ数
    
    up_miss   = 0   # 上側に失敗した回数
    down_miss = 0   # 下側に失敗した回数
    
    x_min = -2.0    # -1.5    # 0.0     # グラフの範囲
    x_max = +2.0    # +1.5    # 1.0
    y_scale = 20    # 10    # 分布曲線をｙ方向に拡大して描く
    
    # N_TRIAL_SET だけ試行セットを繰り返す
    def run(self):
        misses = np.zeros( self.N_TRIAL_SET )
        
        for i in range( self.N_TRIAL_SET ):
            misses[i] = me.each_run()
        
        print( u"信頼区間からの外れ, mean={:.03f}, stdev={:.03f}".format( np.mean(misses), np.std(misses) ) )
        
        plt.xlim( self.x_min, self.x_max )
        self.draw_dist()    # 分布曲線を描き足す
        plt.show()
        
        return
    
    # 分布曲線を描く
    def draw_dist(self):
        n = np.linspace( self.x_min, self.x_max, 1000 )
        p = []
        for i in range(len(n)):
            x = stats.norm.pdf( x=n[i], loc=0, scale=1 )    # 正規分布
            # x = stats.uniform.pdf( n[i], loc=-1, scale=2 )  # 一様分布
            # x = stats.beta.pdf( n[i], 4, 2 )    # ベータ分布
            # x = stats.expon.pdf( n[i], loc=0, scale=1 )  # 指数分布
            # x = stats.cauchy.pdf( n[i] )    # コーシー分布
            p.append( self.y_scale * x )
        
        plt.plot( n, p )
        return
    
    # １回の試行セット
    def each_run(self):
        # print( 'sample_size={}'.format(self.N_SAMPLE) )
        self.up_miss = self.down_miss = 0
        
        means = np.zeros( self.N_TRIAL )
        
        for i in range(self.N_TRIAL):
            means[i] = self.trial()
        
        miss_ratio = (self.up_miss + self.down_miss) / self.N_TRIAL
        print( 'miss_ratio={:.02f}, up_miss={}, down_miss={}, '.format( miss_ratio, self.up_miss, self.down_miss ), end="")
        
        plt.hist( means, color='r', alpha=0.1, histtype='stepfilled' )  # 半透明で重ね書き
        print( 'mean_means={:.05f}, std_means={:.05f}'.format( np.mean(means), np.std(means) ) )
        
        return miss_ratio
    
    # １回の試行
    def trial(self):
        sample = np.random.normal( 0, 1, self.N_SAMPLE ) # N個の正規分布 (平均, 分散, 出力数)
        # sample = np.random.rand( self.N_SAMPLE ) * 2 - 1 # N個の一様乱数
        # sample = np.random.beta( 4, 2, self.N_SAMPLE )   # β分布、非対称でやってみよう
        # sample = np.random.exponential( scale=1.0, size=self.N_SAMPLE )    # 指数分布
        # sample = np.random.standard_cauchy( size=self.N_SAMPLE )    # コーシー分布は平均が無い
        
        real_mean = 0   # 理論上の平均
        # real_mean = 4/(4+2) # a/(a+b) ベータ分布の平均はこうなる
        # real_mean = 1   # 指数分布の平均はscale
        
        # ｔ分布による区間推定
        mean = np.mean(sample)  # 標本平均
        t_dist = stats.t( loc = mean,
                 scale = np.sqrt( np.var(sample, ddof=1) / self.N_SAMPLE ), # √(不偏分散/サンプルサイズ)
                 df= self.N_SAMPLE - 1 )    # 自由度
        down, up = t_dist.interval(alpha=0.95)
        # print( '95% interval: {:.3f} < x < {:.3f}'.format(down, up) )
        
        # 区間推定の結果が当たっているかどうか
        if up < real_mean :
            self.up_miss += 1
        elif down > real_mean :
            self.down_miss += 1
        
        return mean # 標本平均を返す

if __name__ == '__main__':
    me = IntervalCheck()
    me.run()

今年はブログを書くヒマがほとんど無かった。来年はもっと時間のゆとりが欲しい。
それでは、よいお年を！