いまひとつの連分数展開 - 小人さんの妄想

連分数展開という、ちょっとおもしろい計算があります。
こんな感じです。

規則的な連分数展開として、最も有名なのは黄金比 (1+√5)/2 でしょう。
* なぜ黄金比は美しいのか >> d:id:rikunora:20090401
平方根の連分数展開は、規則的に一定の周期を繰り返すということが知られています。
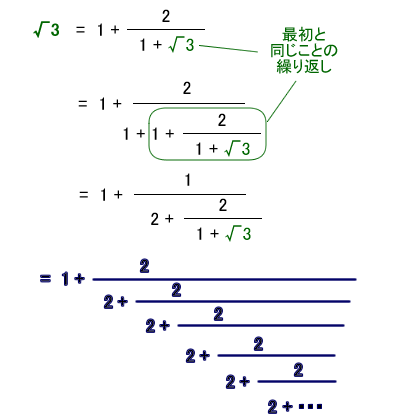
それでは、√3 の連分数展開は、どうなるでしょうか。
ここで私は、√2 の真似をして、こんな計算をしてみました。

見ての通り、分数の部分には２がズラッっと並ぶ形をしています。
なるほど、おもしろい形です。
ところが、ネット上で √3 の連分数展開の結果を検索してみると、たいてい上とは違った答が書いてあります。
試しに、Wolfram|Alpha あたりに"√3" と入力してみて下さい >> http://www.wolframalpha.com/
こんな結果が出てきます。

Wolfram|Alpha では、連分数をこんな記号で書いてあります。
[ 1; 1,2 ]
これは「最初が１で、分数の部分は１と２の繰り返し」という意味です。

上で私の出した、２がズラッっと並ぶ形と、ネット上にある [ 1; 1,2 ] という形は、見かけ上違っています。
まず、[ 1; 1,2 ] という連分数展開ですが、次のように考えれば正しいことがわかります。

ならば、私の出した、２がズラッっと並ぶ形は間違いなのだろうか？
そう思って、２がズラッっと並ぶ形の方を Wolfram|Alpha に入力してみたところ、どうやらこれはこれで合っているようです。
2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/(2 + 2/2))))))))))))))))))))))
0.7320508075689422839681907039419992787868435536829319212738...
√3 の数値は次の通りです。小数点以下12桁まで一致してますね。
1.7320508075688772935274463415058723669428052538103806280558...
つまり、連分数展開の表し方は、１通りではないということです。
その中でも、分子を全て１に揃っているものは特に「正則連分数」と言うのだそうです。wikipedia:連分数
普通に連分数、と呼んでいるものは、正則なもののことだったのですね。

正則ということにこだわらなければ、平方根の連分数展開は、上記の方法で安直にできます。
以下に、√７を３つの方法で連分数展開した結果を挙げます。

この３つは、見かけは異なりますが、どれも√７（に整数を加えたもの）を展開したものになっています。
ちなみに、√７の正規な連分数展開は [ 2 : 1,1,1,4 ] といった４つの数の周期になります。

この「安直な方法」の、最初の式変形は、次のようにして行っています。
例えば √7 - 2 を考えた場合、
　　(√7 - 2)(√7 + 2) = 7 - 2^2 = 3
という式に着目します。
この式の両辺を (√7 + 2) で割れば、√7 - 2 = 3 / (2 + √7) ですね。

１つ疑問に思ったのが、連分数は“約分”できるのだろうか？ということです。
例えば最初の√３の、２がズラッっと並んだ形の式を見てください。
ここに登場する全ての２という数字を、“約分”して一斉に１にできるのでしょうか？
値を確かめてみればわかるのですが、ここで２を１に変えることはできません。
（この√３の連分数展開に現れる２を一斉に１に変えたなら、それは黄金比を表す連分数となってしまいます。）
なので、連分数の“約分”はできないのです。
これも不思議と言えば不思議なことです。
連分数で見えている数字は「足跡」のようなもので、たとえ「足跡」を約分したとしても、
無限の彼方にある「本体」を割ることができないのかな？・・・そんな風に私は思っています。

さて、これで「安直な方法」で平方根を連分数展開する方法はわかったのですが、
反対に、連分数を平方根に戻す方法というものはあるのでしょうか。
実は、上に示したような連分数は、全て二次方程式の答になっています。
なので、繰り返し周期が１の単純な連分数であれば、わりと簡単に値を求めることができます。