サイコロの和と多次元立方体の関係
複数個の一様分布の和は、厳密にはどのような分布に従うのか。
2個のサイコロを同時に振ったとき、最も出やすいのは合計が7のとき。
なぜなら、1+6, 2+5, 3+4, 4+3, 5+2, 6+1 と、6通りの出方があるからです。
それに比べて合計が2となるのは、1+1 の1通り。合計が12となるのは 6+6 の1通りしかありません。
グラフにすれば、このようなテント型になります。

同じようにして、3個のサイコロの和をグラフにまとめると、こんな形になります。

* 計算サイト・サイコロの和の確率
>> http://www.calc-site.com/probabilities/dice_total
さらにサイコロの数を10個、20個と増やしていくと、グラフは滑らかな釣り鐘型曲線へと近づきます。
この釣り鐘型のカーブが「正規分布」なのだ、という話は統計学の教科書に譲るとして、
ここで問題にしたいのは正規分布に至るまでの途中の段階です。
たとえば上のサイコロが3個 ~ 一様分布を3個足し合わせた結果は、厳密にはどのようなカーブなのでしょうか。
あるいは一様分布を7個足し合わせた結果は、正確にはどのような分布なのでしょうか。
先に結果を示します。
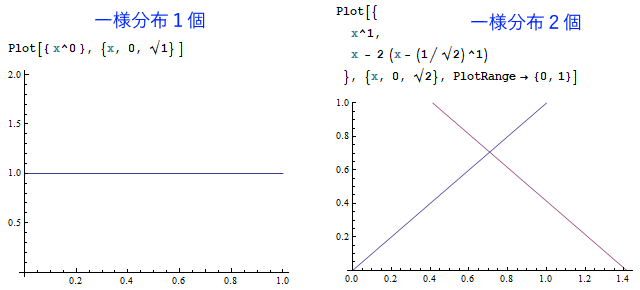
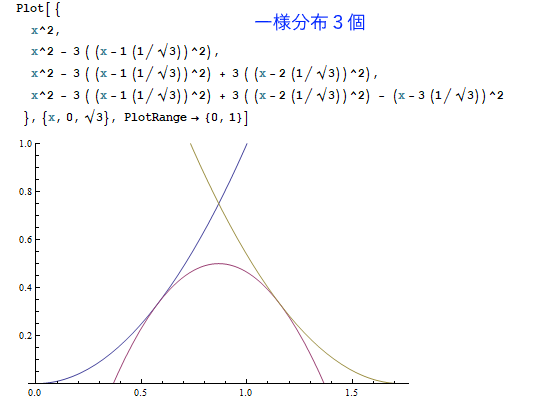
以下は、Mathematicaというソフトで一様分布を1~7個まで足し合わせた結果を描いたものです。
(※ただしグラフの高さは正規化されていません。)
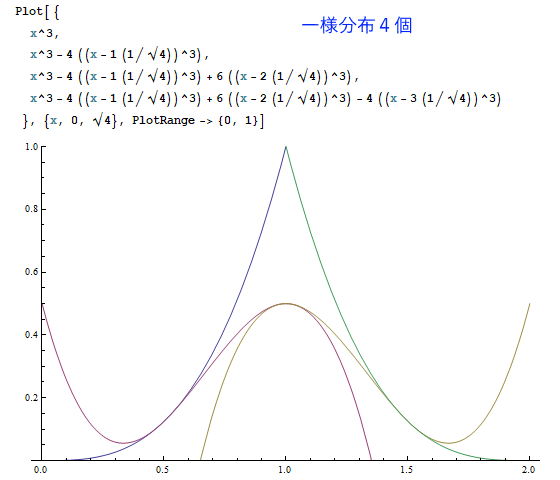
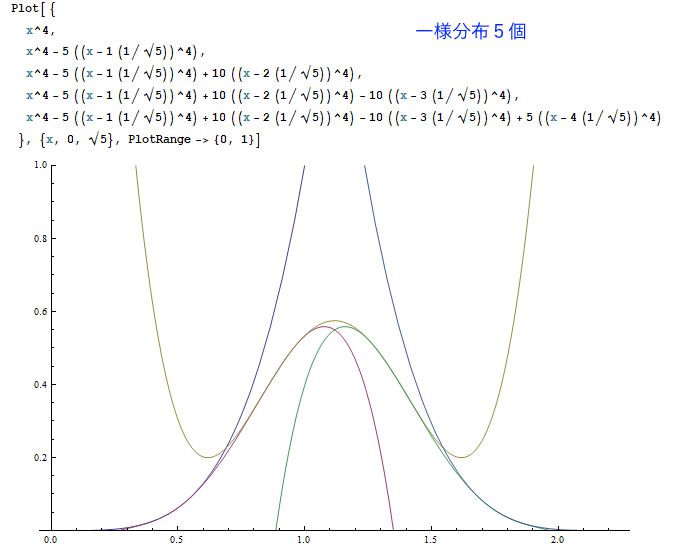
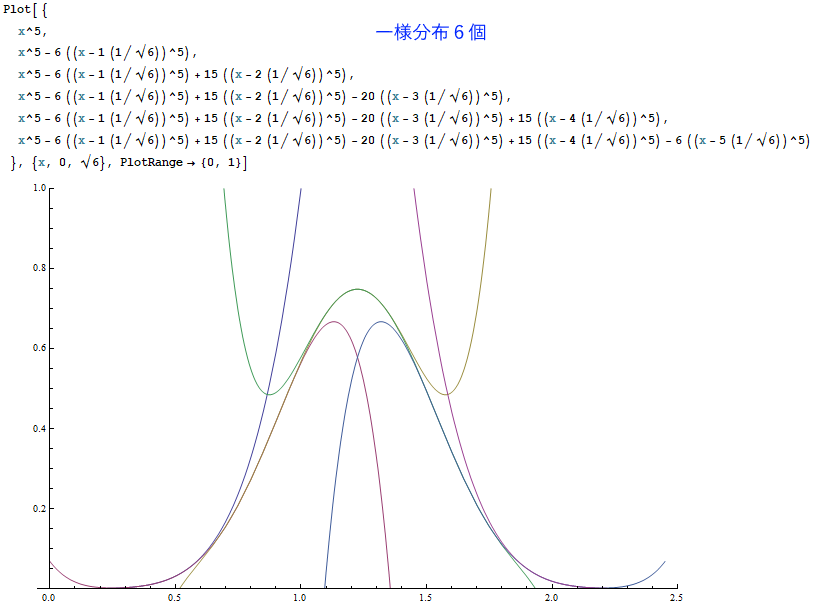
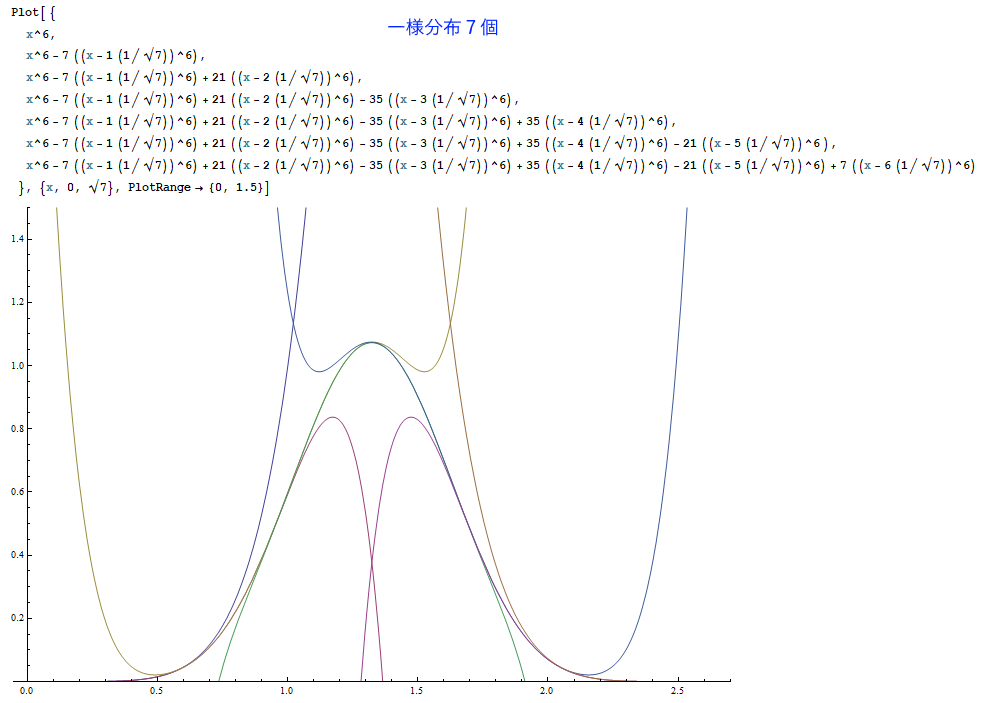
一定の美しい規則に従って、釣り鐘型曲線が削り出される様子が見て取れたでしょうか。
N個の一様分布の和は、N本の(N-1)次曲線の組み合わせから成り立ちます。
たとえばN=3(サイコロ3個)の場合、次の3本の2次曲線で、3つの区間をカバーしています。
y = x^2 -- {x = 0~√3/3 の区間}
y = x^2 - 3 ( (x-1(1/√3))^2 ) -- {x = √3/3~2√3/3 の区間}
y = x^2 - 3 ( (x-1(1/√3))^2 ) + 3 ( (x-2(1/√3))^2 ) -- {x = 2√3/3~√3 の区間}
では、どうやってこれらの曲線を求めたのか。
実はこれらの曲線は、N次元の立方体を、対角線に直行して切った切断面の面積のグラフなのです。
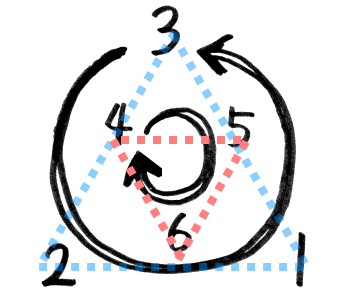
まず2個のサイコロで考えてみましょう。
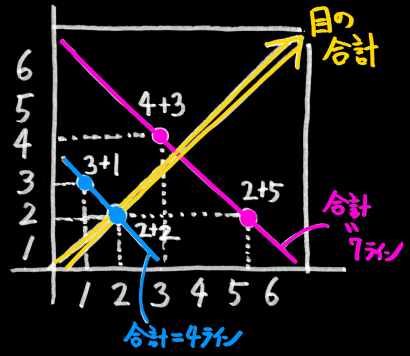
1個目のサイコロの目を横軸に、2個目のサイコロを縦軸に、全ての出目を図示すると6×6の正方形となります。
この正方形の上で、2つの目の合計が一定となる線は、右下がり45度の直線となります。
たとえば、上の図で青で引いた線は合計が4となる直線。
赤で引いた線は合計が7となる直線です。
そして、これらの合計が一定となる直線の長さは、その合計値が出る場合の数=確率に比例しています。
そこで、改めて正方形の黄色い対角線を横軸にして見れば(つまり図を45度傾けて見れば)、
正方形がそのままテント型の分布を形作っていることに気付きます。
次に次元を1つ上げて、3個のサイコロの和を考えてみましょう。
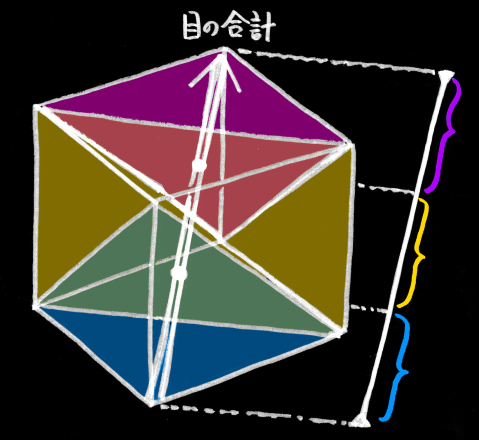
3個のサイコロを3次元の縦、横、高さに配置すれば、6×6×6の立方体となります。
この立方体の上で、3つの目の合計が一定となる面は、立方体の対角線に直行する面となります。
立方体の対角線を軸にして、切断面の面積をグラフに描けば、3個のサイコロ(一様分布)の和の分布となります。
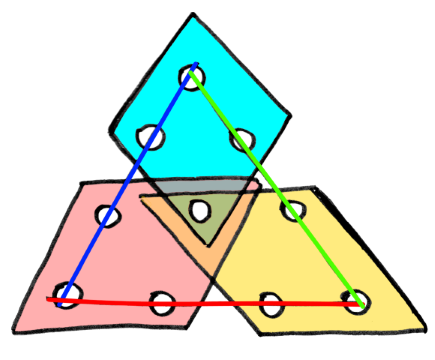
立方体の切断面は、図の手前から順に3つのパートに分かれます。
1番手前の青色のパートは、1つの頂点からスタートし、三角錐がどんどん大きくなる過程。
2番目の中間にある黄色のパートは、断面の正三角形から、もう一方の反対向きの正三角形に向けて、6角形の断面が徐々に変形する過程。
3番目の赤色のパートは、1番目と反対に三角錐がどんどん小さくなる過程です。
1番目と3番目のパートが2次曲線となることは、断面積が辺の長さの2乗となることから想像が付くでしょう。
ちょっと悩むのは2番目の、中間にある6角形断面のパートです。
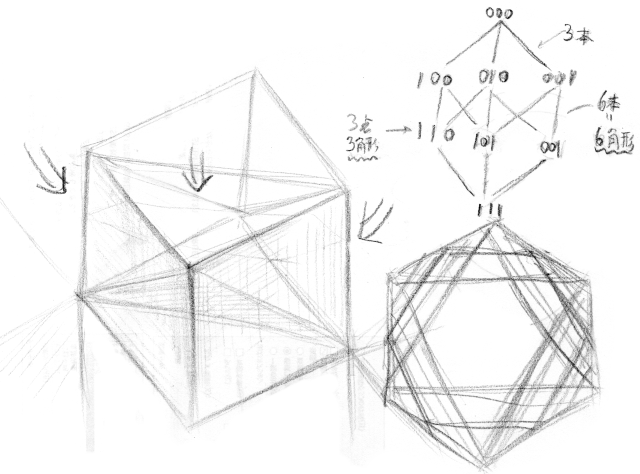
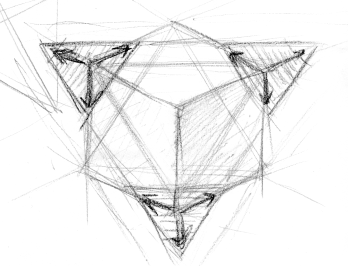
この2枚のスケッチは、6角形断面のパートを取り出して描いたものです。
特に2枚目のスケッチをよく見てください。
断面の6角形とは、拡大する1つの正三角形の3つの頂点から、3つの正三角形を差し引いた残りだと見なせます。
拡大する1つの正三角形と、差し引く3つの正三角形は、実は全く同じ図形を空間的にずらしたものです。
というのも、差し引く3つの正三角形は、元の立方体の隣に位置する、同じ形の立方体の断面だからです。
空間を埋め尽くしている立方体の群れを切断することを想像すれば、
とある1つの立方体の断面積は、同じ形の正三角形を足したり引いたりすることで算出できるのです。
より具体的に、6角形断面の中間パートは次のように定式化できます。
(1番目のパートの正三角形) - 3×(途中から始まった2番目のパートの正三角形)
立方体の対角線の長さは √3 です。
そして、対角線に対する3つのパートの幅はそれぞれ等しく √3/3 ずつです。
なので (途中から始まった…)とは、数字の上では √3/3 だけずらすことを意味します。
以上に基づいて式を完成させたものが、当初に挙げた「一様分布3個」のグラフだったのです。
※3個のサイコロについては、以下がわかりやすいです。
※『ちょっとした「つり鐘型曲線」を描いてみる』
※ https://teenaka.at.webry.info/201704/article_12.html
※『ちょっとした「つり鐘型曲線」と正規分布の関係』
※ https://teenaka.at.webry.info/201704/article_13.html
4個のサイコロ(一様分布)の足し合わせは、4次元立方体を対角線に直行するように切断した断面として表わされます。
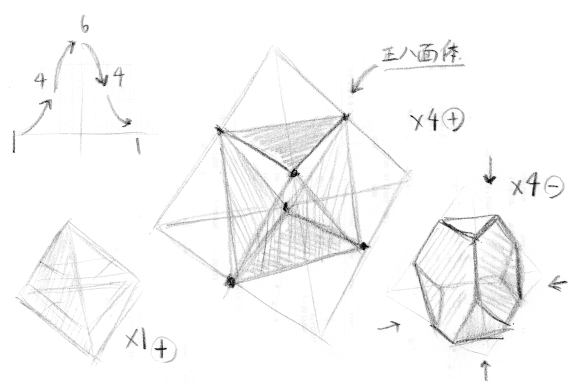
4次元立方体を直接描くことはできませんが、断面である3次元図形を想像することは可能です。
4次元立方体の断面は、以下の4つのパートから成り立ちます。
第1パート:正4面体がだんだん大きくなる過程。
第2パート:正4面体の各頂点が削れ、正8面体となる過程。
第3パート:正8面体の4つの面が成長して、正4面体となる過程。
第4パート:正4面体がだんだん小さくなる過程。
これらの過程は、3次元の場合と同じように、最初の正4面体の足し引きによって定式化できます。
第1パート:(正4面体)
第2パート:(正4面体) - 4×(1つずらした正4面体)
第3パート:(正4面体) - 4×(1つずらした正4面体) + 6×(2つずらした正4面体)
第3パート:(正4面体) - 4×(1つずらした正4面体) + 6×(2つずらした正4面体) - 4×(3つずらした正4面体)
式中に登場する正四面体の数、4、6、4 は、二項係数となっています。
二項係数とは、n個の中からk個の要素を取り出す組み合わせの数のことです。
なぜ二項係数となるのか。
4次元立方体の各頂点に、4桁の0または1で番号を付けることを考えます。
4つの頂点は4つの次元に対して、それぞれ手前と奥のどちらか(あるいは上下、右左などの)一方に位置付けられます。
最も手前にある頂点 0000 から出発して、1111に向かって辺で結ばれた頂点を線で結んでたどってゆくと、以下のような図形が描かれます。
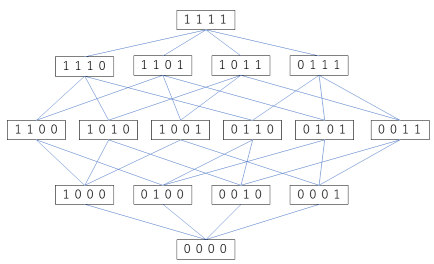
(このような図を“ハッセ図”と言います。)
この図から、同一切断面に並ぶ頂点の数は「4つの桁の中に何個かの1が入る組み合わせの数」になっていることが分かります。
そしてこの頂点の数は、そのまま足し引きすべき図形(正四面体)の数となっているわけです。
以上で見てきた関係は、そのまま次元数が上がっても変わりません。
・最初のパートはN次元の角錐から始まる。グラフの上で、最初の区画は(N-1)次の曲線となる。
・最初のパートの図形(N次元の角錐)を、二項係数に従って足し引することによって、2番目以降のパートをつなげる。
(足し引きは、プラスマイナスを交互に繰り返せばよい。)
こうして、N次元立方体の断面から、N個の一様分布の和が描き出されます。
※ 最初のパートとなるN次元の角錐の体積は、前の記事に記載しました >> d:id:rikunora:20190210
サイコロの数をうんと増やした極限が正規分布になる、ということは、正規分布とは“無限次元立方体の切断面”の形だということになります。
単なるサイコロの足し合わせを、多次元立方体の切断面として捉えるならば、また違った風景が見えてくる。
多次元正三角錐の体積
2次元の正3角形、3次元の正4面体を延長した、4次元空間にある正三角錐の体積はいくつになるか。
さらに延長して、一般にN次元の正三角錐の体積はいくつになるか。
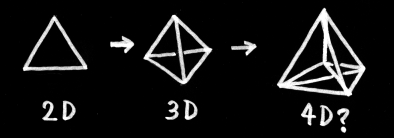
4次元空間にある正三角錐のような図形は、正五胞体というのだそうだ >> wikipedia:正五胞体。
ウィキペディアには『超体積: (√5/96)a^4』と書かれているが、これはどうやって計算したのだろうか。
いきなり4次元では想像が付かないので、目に見える2次元、3次元から類推しよう。
まず2次元の正方形、3次元の立方体を考える。
とある1つの頂点から伸びる辺を全て含むように平面で切り取った角錐のことを“コーナーブロック”と呼ぶことにしよう。
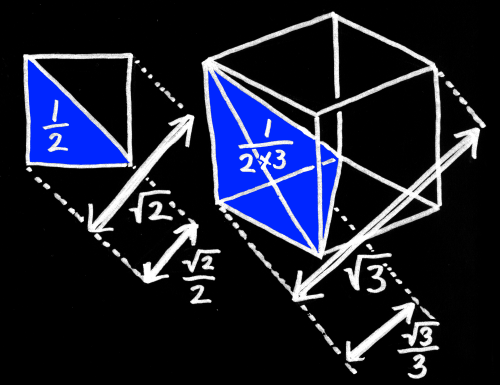
“コーナーブロック”とは、上の図で青く塗った部分のことだ。
2次元の場合は直角2等辺三角形、3次元の場合は切り口が正三角形となるような三角錐である。
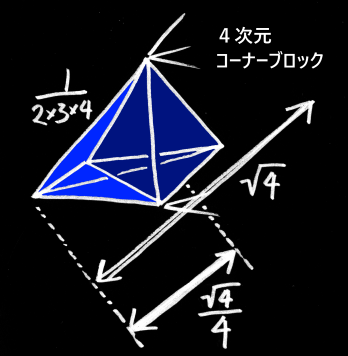
4次元の場合、コーナーブロックの切り口は正4面体になる。
そして5次元であれば、コーナーブロックの切り口は4次元空間にある正三角錐(正五胞体)となる。
つまり、コーナーブロックの切り口が、知りたかったN次元の正三角錐の体積となっているわけだ。
そこで、[コーナーブロックの体積] -> [コーナーブロックの切り口] -> [N次元の正三角錐] という方針で、
N次元の正三角錐の体積を計算してみよう。
コーナーブロックが、もとの立方体の何分の1を占めるかを考えてみる。
2次元の正方形の場合には、見ての通り 1/2 だ。
3次元の立方体の場合には、(1/2)×(1/3) = 1/3! となる。
この延長で、4次元のコーナーブロックを考えると (1/2)×(1/3)×(1/4) = 1/4! になる。
なぜ (1/N次元) が掛け合わされるのか。
たとえば3次元空間の角錐は、1つの立方体を3つの方向に、同じ形に切り分けた一部分なので、元の立方体の 1/3 だと分かる。
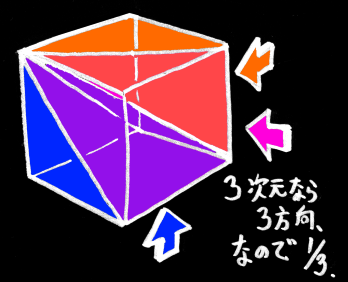
3次元のコーナーブロックは、2次元のコーナーブロックの底面に対して (1/3) を掛けるので、
結局のところ元の立方体の (1/2) × (1/3) となる。
4次元空間は絵には描けないが、きっと4つの方向に同じ形に切り分けた部分なのだから、
3次元のコーナーブロックの底面体に対して 1/4 を掛けたものになる。
以下、N次元空間ならコーナーブロックの体積は、元の立方体の 1/N! になる。
次に、コーナーブロックの、立方体の対角線に対する高さを考える。
2次元の(1辺の長さが1の)正方形の対角線の長さは√2、
3次元の(1辺の長さが1の)立方体の対角線の長さは√3、
N次元の(1辺の長さが1の)超立方体の対角線の長さは√N 。
コーナーブロックの高さは、その対角線の長さの 1/N となる。
2次元であれば、(高さ) = √2/2、
3次元であれば、(高さ) = √3/3 となる。
なぜ、コーナーブロックの高さが、ちょうど対角線の 1/N となっているのか。
その理由は、N次元立方体が等間隔に空間を埋め尽くすからである。
3次元で考えてみよう。
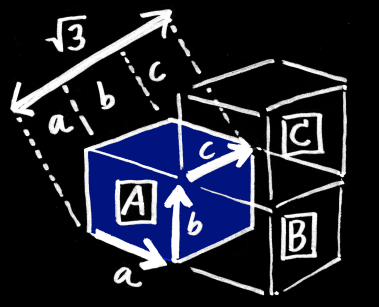
図の立方体[A]に着目して、1つの頂点から反対側の頂点まで、→a, →b, →c と、3本の辺を伝って移動することを考える。
この →a, →b, →c 3本の辺の長さを、立方体[A] の対角線に投影したとき、3本の長さは等しくなる。
たとえば →b を取り上げてみたとき、立方体[A] の隣にある立方体[B] を想像すれば、
→b とは、ちょうど「立方体[B] にとって、立方体[A] の →a 」と同じ位置にある。
なので、→a と →b の、対角線に投影した長さは等しい。
→c についても同じである。
→c とは、ちょうど「立方体[C] にとって、立方体[A] の →a 」と同じ位置にある。
なので結局のところ、元の立方体[A] の対角線は、→a, →b, →c の投影によって3等分される。
この、「立方体が空間を埋め尽くす」という事情は、次元が幾つ上がっても変わらない(だろう)。
なので、N次元のコーナーブロックの高さは、いつでも対角線の 1/N となるわけだ。
以上で、コーナーブロックの体積と高さが分かった。
この体積を高さで微分することによって、切り口の面積(体積?!)を知ることができる。
まず馴染み深い(?!)3次元空間でやってみる。
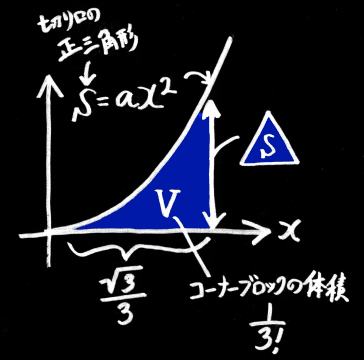
グラフの横軸xは対角線方向の長さ(高さ)、縦軸は切り口の面積S、Sの積分がコーナーブロックの体積Vに相当する。
3次元の場合、切り口の面積は高さの2乗に比例するので、S = a x^2 と置く。(今の時点で a は未知の定数。)
あとは高さxと、体積Vに、上の値を入れて a を計算すればよい。
∫[0~(√3/3)]{ a x^2 }dx = 1/3!
a/3 (√3/3)^3 = 1/6
a = 3√3 / 2
切り口の面積Sは、
a x^2 = (3√3 / 2) (√3/3)^2 = √3/2
これが切り口の正三角形の面積に一致するはずだ。
一辺が1の正三角形の面積は √3/4 なのだが、今考えているコーナブロックの切り口にある正三角形の1辺の長さは√2である。
なので、
S = (√3/4) (√2)^2 = √3/2
確かに一致しているので、どうやらこの方法で良さそうだ。
上と同じことを4次元でやってみよう。
この場合、切り口S には正4面体の体積が現れる。
∫[0~(√4/4)]{ a x^3 }dx = 1/4!
a/4 (1/2)^4 = 1/24
a = 8/3
S = a x^3 = (8/3) (√4/4)^3 = 1/3
1辺が1の正4面体の体積は √2/12。
今求めた切り口S は、一辺が√2の正四面体なので、(√2/12) (√2)^3 = 1/3
確かに一致している。
さらに、5次元でやってみよう。
これで、知りたかった4次元正三角錐の体積が得られる。
∫[0~(√5/5)]{ a x^4 }dx = 1/5!
a/5 (√5/5)^5 = 1/120
a = 25√5/24
S = a x^4 = (25√5/24) (√5/5)^4 = √5/24
これは一辺が√2の4次元正三角錐なので、一辺が1の体積は、
S = (√5/24) / (√2)^4 = √5/96
確かに、Wikipediaに書かれている値と一致した。
以上を一般化して、(N-1)次元の正三角錐の体積が知りたかったなら、
∫[0~(√N/N)]{ a x^(N-1) }dx = 1/N!
a = (√N)^N / (N-1)!
S = a (√N/N)^(N-1) = N^N / {(N-1)! N^(N-1) √N} <-- 一辺が√2 の(N-1)次元の正三角錐
一辺の長さを1にするには、このS を (√2)^(N-1) で割ればよい。
V = S / (√2)^(N-1) = N^N / {(N-1)! (N √2)^(N-1) √N}
正規分布以外の区間推定
t分布を用いた平均値の区間推定には、「正規母集団を仮定する」というただし書きが付いています。
ということは、母集団が正規分布でなかった場合、区間推定は使えないのでしょうか。
母集団の分布は未知であることが多いので、もし正規母集団という条件が絶対だったなら、
区間推定は実際の現場ではほとんど使えない理屈ということになってしまいます。
結論から言えば、たとえ母集団が正規分布で無くても、
母集団から抜き出した標本の平均値が正規分布に従うなら、区間推定の方法を使うことができます。
中心極限定理によれば、ほとんどの分布は(コーシー分布やべき分布といった“平均の無い”分布を除けば)
標本の平均が正規分布に近づくので、区間推定は正規母集団以外にも広く適用可能なのです。
ただし、正規分布から外れるほど大きなサンプルサイズ(データの数)が必要です。
目安は以下の通りです。
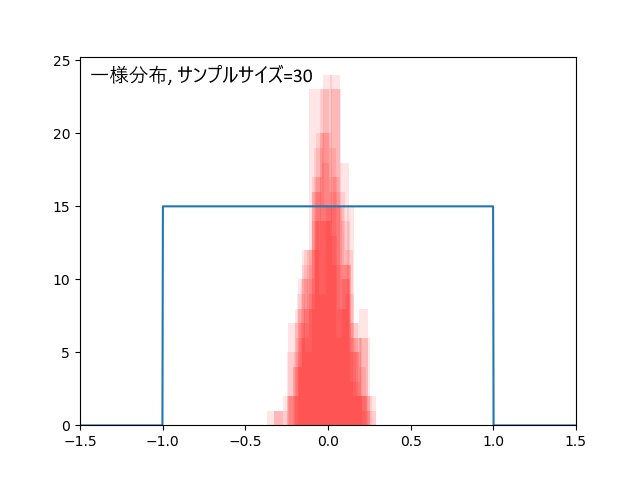
・一様分布なら30個以上
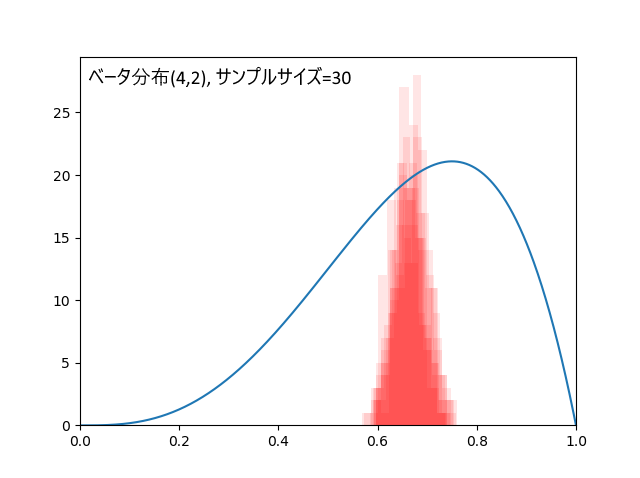
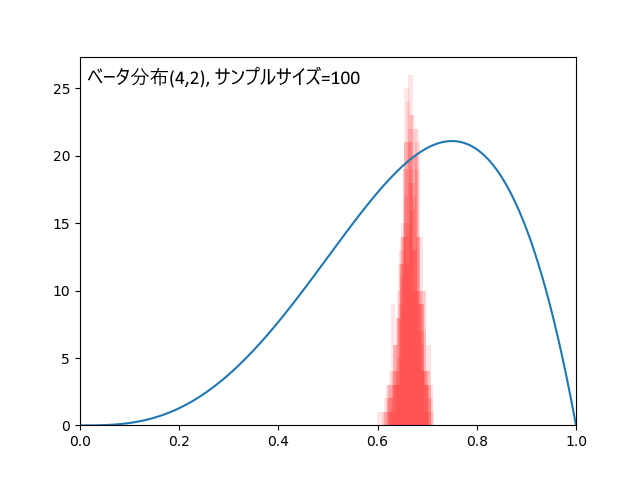
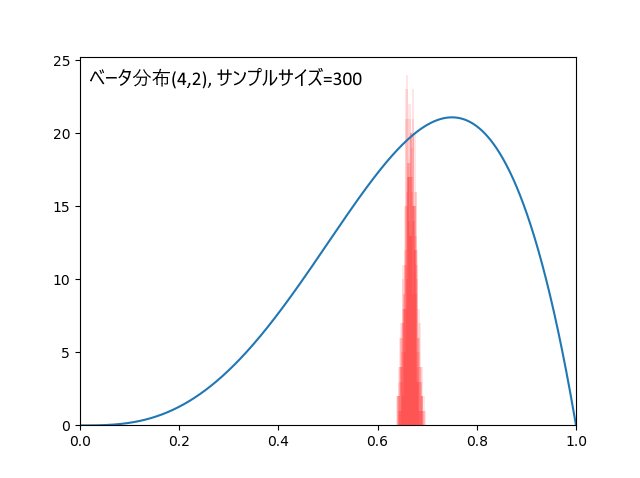
・ベータ分布(a=4,b=2)くらい歪んだ分布なら100個以上
・指数分布のように一方的に偏った分布なら300個以上
これらの目安はどうやって得られたのかというと、ひたすらシミュレーションを繰り返した結果です。
以下に掲げる図は、正規分布以外の特定の分布から、何度も繰り返しサンプルを抜き出して区間推定を行った結果です。
図に示す曲線が元になった母集団の分布。
赤でぼんやり描かれているのは、標本を抜き出す操作を100回繰り返したときの、標本平均のヒストグラムです。
100回の繰り返しを10セット行い、ヒストグラムは10枚重ねて描いてあります。
●正規分布
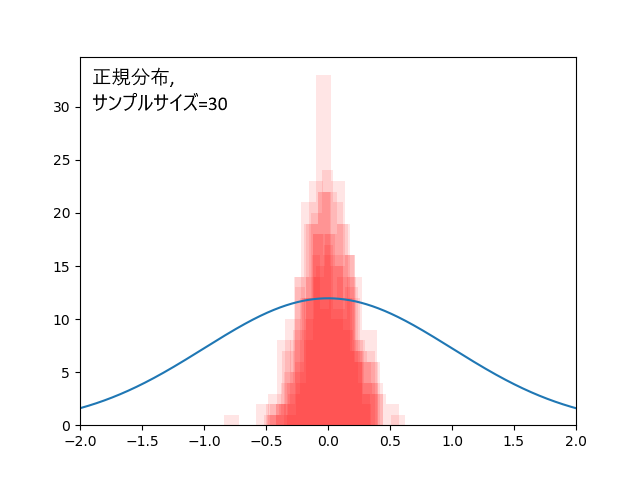
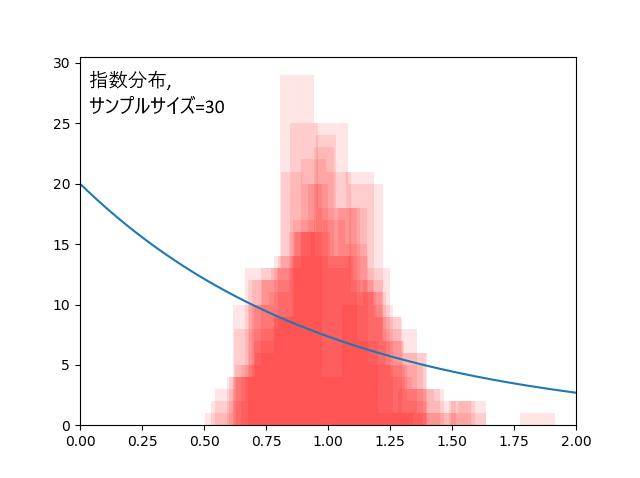
まずこれが正規分布、サンプルサイズ30個の場合。
95%信頼区間であれば、100回のうち95回は真の平均値が信頼区間の中に含まれます。逆に言えば、5回は外れます。
データ30個の場合、外れ回数は5.2回。標本平均の標準偏差=0.18。
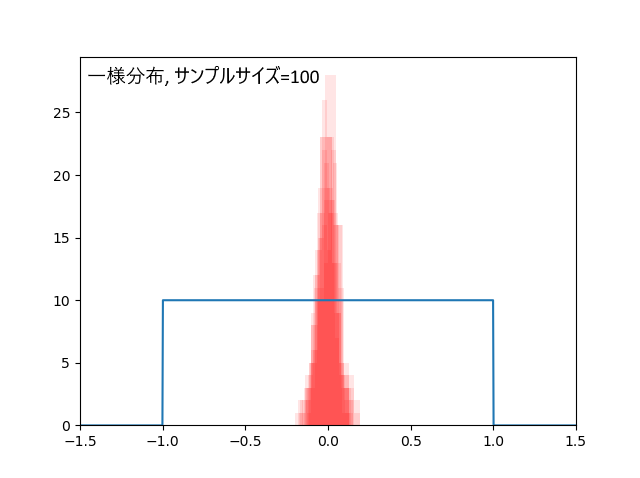
一様分布、データ30個の場合と、100個の場合。
データ数が増えるほど平均値の推定幅が小さくなる様子が見てとれます。
データ30個の場合、外れ回数は4.5回。標本平均の標準偏差=0.10。
データ100個の場合、外れ回数は5.2回。標本平均の標準偏差=0.06。
データ数30個であっても区間推定は十分有用でした。
ベータ分布(4,2)、真の平均値は0.666...、歪んだ分布の例として取り上げました。
データ30個の場合、外れ回数は4.2回。標本平均の標準偏差=0.031。
データ100個の場合、外れ回数は5.5回。標本平均の標準偏差=0.018。
データ300個の場合、外れ回数は4.9回。標本平均の標準偏差=0.010。
30個だと結果が不安定(ばらつきが大きい)でしたが、100個あればかなり安定します。
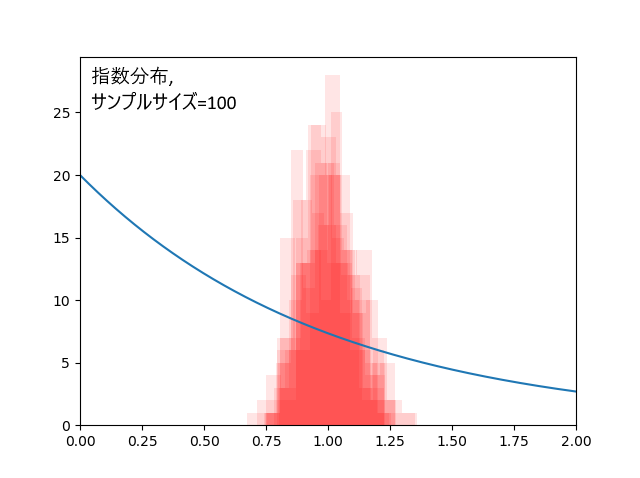
指数分布、真の平均値は1。
データ30個の場合、外れ回数は8.7回。標本平均の標準偏差=0.18。
データ100個の場合、外れ回数は6.6回。標本平均の標準偏差=0.10。
データ300個の場合、外れ回数は5.3回。標本平均の標準偏差=0.06。
元の分布がここまで偏っていたなら、安定した結果には300個のデータが欲しいところです。
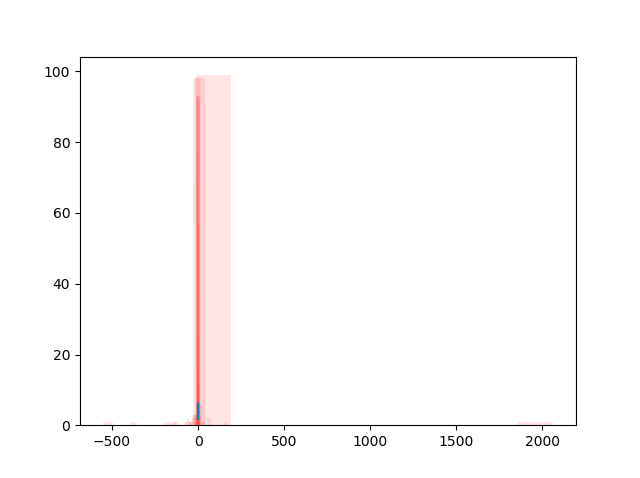
コーシー分布には“平均値がありません”。なので、区間推定は使えません。
上はデータ30個の場合ですが、確かに見ての通り、区間推定は適用できません。
* コーシー分布とarctan微分 >> [id:rikunora:20171210]
検索したところ、ここに詳しく書かれていました。
* 大人の知らない統計学 6 非正規分布の信頼区間
>> https://blogs.yahoo.co.jp/pironotakarabako/63655916.html
以下にシミュレーションのソースを示します。
(分布や数値の付け替えはコメントで行っています。わかりずらい。)
シミュレーションといっても、要は区間推定をひたすら繰り返しているだけです。
# -*- coding: utf-8 -*- """ 区間推定の頑健性、正規母集団以外では、どれほどサンプルがあれば妥当なのか。 """ import numpy as np from scipy import stats import matplotlib.pyplot as plt class IntervalCheck: N_TRIAL_SET = 10 # 試行セット回数 N_TRIAL = 100 # 試行回数 N_SAMPLE = 30 # 100 # 300 # サンプルサイズ=データ数 up_miss = 0 # 上側に失敗した回数 down_miss = 0 # 下側に失敗した回数 x_min = -2.0 # -1.5 # 0.0 # グラフの範囲 x_max = +2.0 # +1.5 # 1.0 y_scale = 20 # 10 # 分布曲線をy方向に拡大して描く # N_TRIAL_SET だけ試行セットを繰り返す def run(self): misses = np.zeros( self.N_TRIAL_SET ) for i in range( self.N_TRIAL_SET ): misses[i] = me.each_run() print( u"信頼区間からの外れ, mean={:.03f}, stdev={:.03f}".format( np.mean(misses), np.std(misses) ) ) plt.xlim( self.x_min, self.x_max ) self.draw_dist() # 分布曲線を描き足す plt.show() return # 分布曲線を描く def draw_dist(self): n = np.linspace( self.x_min, self.x_max, 1000 ) p = [] for i in range(len(n)): x = stats.norm.pdf( x=n[i], loc=0, scale=1 ) # 正規分布 # x = stats.uniform.pdf( n[i], loc=-1, scale=2 ) # 一様分布 # x = stats.beta.pdf( n[i], 4, 2 ) # ベータ分布 # x = stats.expon.pdf( n[i], loc=0, scale=1 ) # 指数分布 # x = stats.cauchy.pdf( n[i] ) # コーシー分布 p.append( self.y_scale * x ) plt.plot( n, p ) return # 1回の試行セット def each_run(self): # print( 'sample_size={}'.format(self.N_SAMPLE) ) self.up_miss = self.down_miss = 0 means = np.zeros( self.N_TRIAL ) for i in range(self.N_TRIAL): means[i] = self.trial() miss_ratio = (self.up_miss + self.down_miss) / self.N_TRIAL print( 'miss_ratio={:.02f}, up_miss={}, down_miss={}, '.format( miss_ratio, self.up_miss, self.down_miss ), end="") plt.hist( means, color='r', alpha=0.1, histtype='stepfilled' ) # 半透明で重ね書き print( 'mean_means={:.05f}, std_means={:.05f}'.format( np.mean(means), np.std(means) ) ) return miss_ratio # 1回の試行 def trial(self): sample = np.random.normal( 0, 1, self.N_SAMPLE ) # N個の正規分布 (平均, 分散, 出力数) # sample = np.random.rand( self.N_SAMPLE ) * 2 - 1 # N個の一様乱数 # sample = np.random.beta( 4, 2, self.N_SAMPLE ) # β分布、非対称でやってみよう # sample = np.random.exponential( scale=1.0, size=self.N_SAMPLE ) # 指数分布 # sample = np.random.standard_cauchy( size=self.N_SAMPLE ) # コーシー分布は平均が無い real_mean = 0 # 理論上の平均 # real_mean = 4/(4+2) # a/(a+b) ベータ分布の平均はこうなる # real_mean = 1 # 指数分布の平均はscale # t分布による区間推定 mean = np.mean(sample) # 標本平均 t_dist = stats.t( loc = mean, scale = np.sqrt( np.var(sample, ddof=1) / self.N_SAMPLE ), # √(不偏分散/サンプルサイズ) df= self.N_SAMPLE - 1 ) # 自由度 down, up = t_dist.interval(alpha=0.95) # print( '95% interval: {:.3f} < x < {:.3f}'.format(down, up) ) # 区間推定の結果が当たっているかどうか if up < real_mean : self.up_miss += 1 elif down > real_mean : self.down_miss += 1 return mean # 標本平均を返す if __name__ == '__main__': me = IntervalCheck() me.run()
今年はブログを書くヒマがほとんど無かった。来年はもっと時間のゆとりが欲しい。
それでは、よいお年を!
エクセル近似曲線の罠
エクセル近似曲線の「指数近似」「累乗近似」は、いわゆる非線形最小二乗法ではない。
・エクセルで用いているのは、データの対数に直線をあてはめるという方法。
・いわゆる非線形最小二乗法とは、残差(誤差)の2乗和を最小にする方法。
詳しいことは以下のページで尽きているのだが、エクセルの近似曲線は便利だと、
私自身多くの人に勧めている手前、注意を忘れないよう記載しておく。
* Excelグラフ累乗,指数,多項式近似の論文記載の注意(生物科学研究所 井口研究室)
>> https://biolab.sakura.ne.jp/excel-graph.html
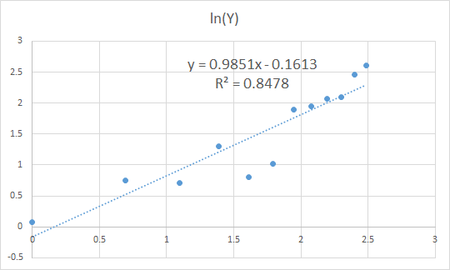
赤い点で描かれているのが元になるデータ、
Y = 0.8 * exp( 0.3 * X ) に、Xに比例する大きさで正規乱数を加えたもの。
下側の青い線がエクセルの指数近似曲線。
上側の緑の線はR言語による非線形回帰。
赤い点で描かれているのが元になるデータ、
Y = 0.3 * X ^ 1.5 に正規乱数を加えたもの。
直線に近い青い線がエクセルの累乗近似曲線。
よりカーブのきつい、緑の線はR言語による非線形回帰。
ぱっと見に、あてはまりが良さそうなのはR言語の方に思える。
だからといってエクセルが“間違っている”というわけでもない。
エクセルはR言語と異なる方法で線を引いているのである。
R言語がもともとの回帰式の上で誤差を最小化するのに対し、
エクセルは両辺対数をとった式の上で誤差を最小化する。
* 指数近似
Y = a * X ^ b -- もともとの回帰式
ln(Y) = ln(a) + b ln(X) -- 両辺対数をとった式
* 累乗近似
Y = a * exp(b * X) -- もともとの回帰式
ln(Y) = ln(a) + b * X -- 両辺対数をとった式
もともとの回帰式は曲線だが、両辺対数をとった式は直線となる。
誤差の最小化は、直線の方がずっと簡単だ。
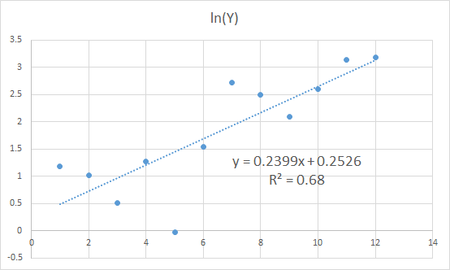
直線に直した上での回帰は以下のようになる。
この直線で求めたパラメータが、エクセル近似曲線のものに一致していることが見て取れる。
※ exp(0.2526)=1.2874, exp(-0.1613)=0.851
エクセル近似曲線は、直線回帰にちょっとオマケを付け足して実現した機能だったのだ。
エクセルの指数近似、累乗近似では、ゼロやマイナスを含むデータに線を引くことができない。
なぜできないかというと、ゼロやマイナスの対数がとれないからである。
また、エクセルには指数回帰を行う"LOGEST"という関数があるが、この関数で求めた数字も、近似曲線で求めた数字と同じである。
(もう1つの、直線回帰のための"LINEST"関数は特に問題無い。)
さらに、エクセルでは近似曲線に対して決定係数R2を計算することができるのだが、
決定係数R2は本来、線形回帰についてのあてはまり指標であり、非線形回帰に用いることはできない。
では、エクセルに出てくる決定係数は何なのかというと、対数をとって直線に直したときの決定係数だったのだ。
なので、この数字をうのみにして、そのまま用いるべきではない。
非線形回帰であてはまりの良さを評価するには、決定係数ではなく、
残差の2乗和、あるいは(回帰分析の)標準誤差を用いるのが妥当だ。
以上の懸念は、指数近似、累乗近似の話であって、他の種類の曲線「対数近似」「多項式近似」では心配しなくてよい。
実際試してみると、対数近似、多項式近似の結果はR言語と一致する。
なぜそうなるかというと、
・対数近似,多項式近似 は 線形回帰
・指数近似,累乗近似 は 非線形回帰
だからである。
形の上で、線形=直線、非線形=曲線、と思い込んでいる人もいるかもしれないが、
回帰分析の場合、回帰式が推定パラメータについて1次のものが線形、そうでないものが非線形である。
・対数近似の回帰式: y = a ln(X) + b
・多項式近似の回帰式: y = a X^2 + b X + c
いずれの回帰式も(Xではなく)a, b, c については1次式となっている。
で、指数近似,累乗近似がやりたかったとき、結局のところどうすれば良いのか。
・エクセルを使ったときは、エクセルの結果だと明記しておく。
・できればR言語、あるいは信頼できる統計用ソフトを使った方が良い。
・実はエクセルの「ソルバー」機能を使えば、非線形回帰も不可能ではない。
でも、そこまでするなら素直にR言語使えば良いのではないかな。
* Excelのチャートオプション"近似曲線の追加"機能の評価
>> https://ci.nii.ac.jp/naid/110007025777
以下はR言語上での操作です。
### 累乗近似、非線形回帰 # データを用意 x <- c(1:12) y <- c( 1.075513124, 2.104125184, 2.045615008, 3.70051273, 2.221801362, 2.769819828, 6.656385201, 7.037107115, 7.976938733, 8.150842204, 11.70331758, 13.66264136 ) nonline <- nls( y ~ a * x^b, ,start=c(a=1,b=1)) # 非線形回帰 summary(nonline) # 結果の要約 Formula: y ~ a * x^b Parameters: Estimate Std. Error t value Pr(>|t|) a 0.2680 0.1204 2.226 0.0502 . b 1.5587 0.1959 7.957 1.23e-05 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 1.132 on 10 degrees of freedom Number of iterations to convergence: 8 Achieved convergence tolerance: 2.96e-06 # プロットしてみる a <- coef(nonline)[1] b <- coef(nonline)[2] plot( y ~ x) curve( a*x^b, add=T, col="red") ### 指数近似、非線形回帰 # データを用意 x <- c(1:12) y <- c( 3.283583359, 2.754235941, 1.674398192, 3.556187361, 0.976339451, 4.652897765, 15.21122786, 12.09124224, 8.109277666, 13.59872153, 23.046961, 24.17609857 ) nonline <- nls( y ~ a * exp(b*x), ,start=c(a=1,b=1)) # 非線形回帰 summary(nonline) # 結果の要約 Formula: y ~ a * exp(b * x) Parameters: Estimate Std. Error t value Pr(>|t|) a 1.53717 0.67319 2.283 0.045521 * b 0.23269 0.04152 5.605 0.000226 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 3.404 on 10 degrees of freedom Number of iterations to convergence: 15 Achieved convergence tolerance: 3.005e-07 # プロットしてみる a <- coef(nonline)[1] b <- coef(nonline)[2] plot( y ~ x) curve(a * exp(b*x), add=T, col="red")
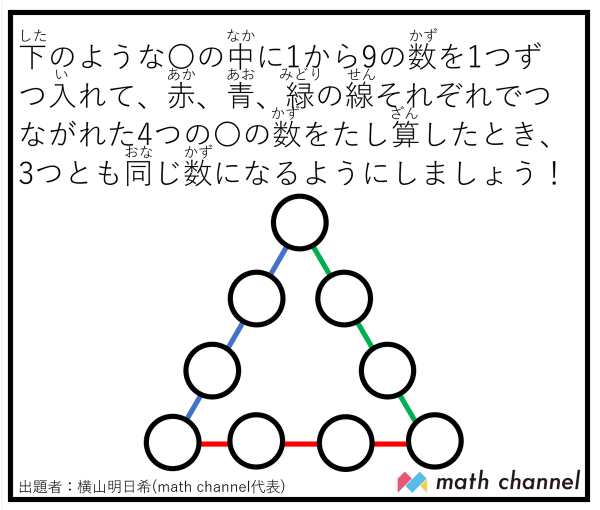
10個の数字の計算パズル
「日本お笑い数学協会」というTwitterに流れていた問題 >> https://twitter.com/owaraisugaku?lang=ja
気になったのでメモを書き残して仕事に出かけて、帰ってきたら家族がものすごく計算してた!

>> https://ameblo.jp/rikunora/entry-12420444729.html
で、私と言えばオヤジのメンツを保つため、こっそりパソコンの力で解いたのはここだけの秘密です。
※ 以前紹介した Coprisで解けます(下を参照)>> [id:rikunora:20181025]
※(答えるときはリプライは避け、引用RTなどでお願いします!)とあったので、答は載せません。
同じTwitterに、こんな問題もありました。
やはりパソコンの力を借りて答を列挙したところ、
合計 17 となる答が 2 通り、
合計 19 となる答が 4 通り、
合計 20 となる答が 6 通り、
合計 21 となる答が 4 通り、
合計 23 となる答が 2 通り、
全部で18通りの答がありました。
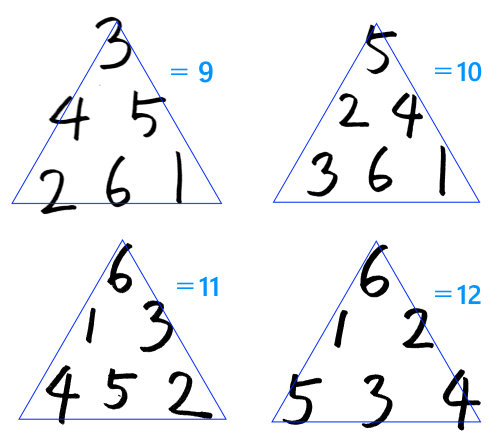
いきなり上の三角形に挑むのは少々しんどいので、もう1段簡単にした問題で考えてみました。
答は以下の4通り。
よく見ると並び方に規則があります。
これをもとにすれば、先の1段階大きな三角形でも何とかなると思う。
せっかくなので、私も1問考えてみました。
答は2通りある。
ヒント:合計は 19 になる。
/** * □□÷□=□□÷□=□×□=□□を解く Scala + Copris スクリプト. */ import jp.kobe_u.copris._ import jp.kobe_u.copris.dsl._ // 10個の変数を用意する for( n <- 0 until 10 ){ int('x(n), 0, 9) // 0〜9の整数 } // 10個は全て異なる var lst = List[Term]() for( n <- 0 until 10 ){ lst :+= 'x(n) } add( Alldifferent( lst ) ) // 問題の式 var last_term = 'x(8) * 10 + 'x(9) add( ('x(0) * 10 + 'x(1)) === 'x(2) * last_term ) // 割り算は直接書けないので add( ('x(3) * 10 + 'x(4)) === 'x(5) * last_term ) add( 'x(6) * 'x(7) === last_term ) /* 10の位は0にならない。0で割り算しない。この条件は無くても可 ** 'x(0) !== 0 'x(2) !== 0 'x(3) !== 0 'x(5) !== 0 'x(8) !== 0 **/ find printf( "%d%d ÷ %d = %d%d ÷ %d = %d × %d = %d%d\n", solution('x(0)), solution('x(1)), solution('x(2)), solution('x(3)), solution('x(4)), solution('x(5)), solution('x(6)), solution('x(7)), solution('x(8)), solution('x(9)) )
公平な不平等、不公平な平等
長さ1000cmの棒を一様乱数で1000個に切り分けたら、どんな長さの破片ができるか?
1cmの破片が1000個できるのかな、と想像しがちなところですが、実際にはこうなります。
これはパソコンでシミュレーションした結果のヒストグラムです。
確かに破片1個の“平均”は1cmなのですが、数で言えば平均以下の小さい破片の方がずっと多く、
その一方で、ごく小数の極端に長い破片があります。
最も数が多いのは、最も短い0.0〜0.18cmで、ここに160個以上の破片が含まれています。
反対に、最も長いものは 8cm以上、次いで7cm台、6cm台にも、ごく少数の破片があります。
以上は、ほんの数行のPythonスクリプトで確かめることができます。
# 長い棒を一様乱数で切ったら、破片の分布はどうなる? import numpy as np import matplotlib.pyplot as plt rds = np.sort(np.random.rand(1000) * 1000) # 1000個の乱数をソート sample = [ rds[i+1] - rds[i] for i in range(rds.size-1) ] # 乱数の間隔を取得する sample[-1] = rds[0] + (1000 - rds[-1]) # 最後は末尾と先頭をつなげる plt.hist( sample, bins=50 ) plt.show()
たとえPytonを知らなくても、エクセルで1000個の乱数を作って試すこともできます。
手間を厭わなければ、実験して確かめることもできます。 >> [id:rikunora:20091213]
これがタイトルに掲げた「公平な不平等」です。
乱数は公平です。しかし、公平な乱数で分配した結果は、不平等なのです。
“公平=平等”という思い込みは、必ずしも正しくありません。
似たようなことを、交換によって確かめてみましょう。
・1000人が当初1.0ずつの財産を持ち、お互いにランダムに財産を交換する。
・交換は、ランダムに選んだ2人がお互いの財産を出し合い、それを一様乱数によって振り分ける。
・交換を10万回繰り返す。
結果はこうなりました。
赤い線は「指数分布」と呼ばれている曲線で、理論上はこうなる、という形です。
さらに、交換のルールを少し変えてみましょう。
・1000人が当初1.0ずつの財産を持ち、お互いにランダムに財産を交換する。
・交換は、ランダムに選んだ2人が少ない方を越えない財産を出し合い、それを一様乱数によって振り分ける。
・交換を10万回繰り返す。
先ほどとの違いは「少ない方を越えない」という点で、たとえ少ない方が負けても全財産を失わないようにとの配慮からです。
結果は極端で、ごく一握りの勝ち組以外、大半はほとんど0になります。
なぜこうなるかと言うと、いったん財産が0近くになると、そこから抜け出すのが極めて困難だからです。
これでは余りにも勝ち負けがはっきりしているので、ハンディを付けましょう。
・交換は、ランダムに選んだ2人の財産の2乗の和が一定になるように乱数で振り分ける。
どういうことかと言うと、金持ちは持てる財産の大きさに比例してハンディを負え、というルールです。
先ほどより、だいぶ平等に近づきました。
※ 赤い線は「ガンマ分布」と呼ばれている曲線です。
※ なんとなく当てはまりそうですが、理論的にこれが正解なのかどうか、私にはよく分かりません。
もっともっとハンディを付けたら、どうなるか。
・交換は、ランダムに選んだ2人の財産の3乗の和が一定になるように乱数で振り分ける。
金持ちは持てる財産の2乗に比例してハンディを負えという、かなり金持ちに厳しいルールです。
さらに平等に近づいてきました。
反対に、金持ちが有利になるようなハンディを付けてみたら、どうなるか。
・交換は、ランダムに選んだ2人の財産の平方根の和が一定になるように乱数で振り分ける。
予想通り、かなり不平等な結果となりました。
以上の結果をまとめて描くと、こうなります。
このグラフは、分配ルールのハンディ乗数を0.5(平方根)〜4.0まで、0.5刻みに変えた結果を重ねて描いたものです。
(人数は8000人に増やしています。)
ハンディの大きさに応じて、結果が格差から平等に変わる様子が見て取れることと思います。
昔から言い古されてきたことなのですが、自由とは格差社会であり、かといって出る杭を打つ社会に生まれた天才は不幸です。
この事実は今も昔も変わりませんが、今が昔と違うところは、分配ルールによって平等が調整できる姿を、誰もがパソコン1つで試せるようになったことです。
不平等とは、地震や台風のようにコントロール不能な災害ではなく、人がコントロールできる問題です。
もし効率を求める組織だったなら、結果としての不平等より、チャンスとしての公平を敷くべきかもしれません。
あるいは調和を求める社会だったなら、結果としての平等を重んじ、方法としての不公平を受け入れるべきかもしれません。
ひょっとすると、全体最適化のためには適切なセグメンテーション、クラス分けや階級化が必要なのかもしれません。
いずれにせよ、目的に叶ったルールは数字の上で選択可能であり、
たとえそのモデル化が不完全だったとしても、感情にまかせた言葉をぶつけ合うよりずっと合理的だと思うのです。
* なぜ統計学では釣り鐘型の分布が使われ、物理現象では右肩下がりの分布が使われるのか
>> [id:rikunora:20170321]
# 交換のルールを変えてみたら、分布はどのように変わるのか import numpy as np import random import scipy.optimize import matplotlib.pyplot as plt class ExchgRule: # 2つの数の合計をランダムに分配する def exchg(self, a, b): rd = np.random.rand() s = a + b p = (s * rd) q = (s * (1.0 - rd)) return ( p, q ) # 小さい方の数と等量(双方が出せるだけの金額)をランダムに分配する def exchg_min(self, a, b): rd = np.random.rand() mn = min( a, b ) mx = max( a, b ) p = 2 * mn * rd q = 2 * mn * (1-rd) return ( p, q + mx - mn ) # 2つの数のn乗の和が一定になるように分配する def exchg_pwn(self, a, b, n): rd = np.random.rand() s = np.power(a, n) + np.power(b, n) p = np.power(s * rd, 1/n ) q = np.power(s * (1.0 - rd), 1/n ) ratio = (a+b) / (p+q) # 合計が一定となるように標準化 return( ratio * p, ratio * q ) def run(self): N_SAMPLE = 1000 # 粒子数 N_EXCHG = 100000 # 交換回数 # フィットさせたい関数、指数分布 def exfunc(x, a, b): return a * np.exp( - x * b ) # TypeError: only size-1 arrays can be converted to Python scalars # mathパッケージのlogやexpを用いるとエラーが出ます。 # numpyパッケージのlogやexpを用いればオッケーです。 # フィットさせたい関数、正規分布 def nmfunc(x, a, b, c): return a * np.exp( - (x-c)**2 * b ) # フィットさせたい関数、ガンマ分布っぽいもの def gmfunc(x, a, b, c): return a * np.power(x, b) * np.exp( - x * c ) # いろんな分布からスタートしてみる sample = np.random.rand(N_SAMPLE) # 一様分布 # sample = np.random.randn(N_SAMPLE) # 標準正規分布 # sample = np.random.normal( 10, 2, N_SAMPLE ) # 正規分布、平均をずらした # sample = np.random.exponential( scale=1.0, size=N_SAMPLE ) # 指数分布 sample = np.abs( sample ) # 絶対値に直す for i in range(N_EXCHG): a, b = random.sample( range(N_SAMPLE), 2 ) # ランダムに2つの数を選ぶ # p, q = self.exchg( sample[a], sample[b] ) # p, q = self.exchg_min( sample[a], sample[b] ) # 双方が出せるだけを分配 p, q = self.exchg_pwn( sample[a], sample[b], 2 ) # n乗だったらどうなる sample[a] = p sample[b] = q ret = plt.hist( sample, bins=50 ) # ヒストグラムを描く # 曲線あてはめを試みる fit_func = exfunc # exfunc # gmfunc # 関数名が直接代入できるって便利. hist_x = ret[1][:-1] # ヒストグラムの結果は返り値に入っている hist_y = ret[0] param, cov = scipy.optimize.curve_fit( fit_func, hist_x, hist_y ) print( param ) fit_y = fit_func( hist_x, *param ) plt.plot( hist_x, fit_y, '-', color="red") # 曲線を描く plt.show() print( "ave={:.05f}, std={:.05f}, {:.05f}〜{:.05f}".format( \ np.mean(sample), np.std(sample), np.min(sample), np.max(sample)) ) if __name__ == '__main__': me = ExchgRule() me.run()
総合順位が個々の最高順位よりも上となる確率
たとえばトライアスロン3種目で、総合順位が個々の種目のどの順位よりも上になることがある。
これはちょっと意外に思えるので、問題をうんと単純化して2種目で考えてみよう。
赤、青、黄の3人の、数学と英語のテスト結果が上の図のようだったとすると、
青は数学でも2位、英語でも2位でありながら総合順位は1位だ。
なので、(総合順位) > (個々の種目の最高順位) はあり得ることなのだ。
しかし下の図のような状況だと、青が総合1位となるには、英語、数学のどちらかで1位を取らないといけない。
なので、総合順位が上になるかどうかは、周囲の状況で変わってくる問題だったのだ。
さて、トライアスロン3種目の場合は、2種目で線で描いた状況を、立体化して面で描けば良いわけだ。
赤と黄に足を引っ張る不得意種目があったなら、平均的な青が総合1位なることだってあり得る。
では、総合順位が個々の最高順位よりも上となる人は、全体のうちどれくらい居るのだろうか。
ちょっと考えても分からなかったので、パソコンでシミュレーションを行った結果がこれ。
2科目の場合、全体の 1/3 が、
3種目の場合、全体の 1/4 が、
N種類の場合、全体の 1/(N+1) が、
個別の順位よりも総合順位の方が上という、シンプルな結果となった。
この結果からすると、
・種目数が少なければ、突出せずとも満遍なくこなす人が上位に行くことがある。
・種目数が多くなるにつれて、どの分野でも負けないだけでは不十分で、突出した得意分野が望まれる。
以上、シミュレーションの結果は間違い無いだろうと思っているが、
ではなぜ全体の 1/(N+1) となるのか、きちんとした証明ができていない。
2科目、3種目の図を見ると、なんとなく分かるような気もするのだが、うまく説明できない。
誰か賢い人、考えてみて。
# -*- coding: utf-8 -*- """ 総合力ってどのくらいあるの? たとえばトライアスロン3種目で、総合順位が個々の種目の最高順位よりも上となる確率は? """ import numpy as np from statistics import mean class GeneOrder: N_MEMBER = 5000 # 参加人数 # 競技の数を2〜15まで変えて試してみる def run(self): for n_subj in range( 2, 16 ): # 競技の数を変えてみる results = [] for repeat in range( 10 ): # 10回繰り返して平均をとる ret = self.each_run( n_subj ) results.append( ret ) # print( results ) val = mean(results) pred = 1/(n_subj+1) # 結果はおそらく1/(競技数+1) になると予想 # 競技数, 実験値, 予想値, 食い違い print( "{}, {:.5f}, {:.5f}, {:.05f}".format( n_subj, val, pred, val-pred ) ) # 個々の試行 # n_sub: 競技の数 def each_run(self, n_subj): points = [] # 各種目ごとの得点配列 orders = [] # 各種目ごとの順位配列 # 各種目について得点を付ける for i in range( n_subj ): # いろんな分布で試してみよう x_arr = np.random.rand( self.N_MEMBER ) # N個の一様乱数 # x_arr = np.random.normal( 0, 1, self.N_MEMBER ) # N個の正規分布 (平均, 分散, 出力数) # x_arr = np.random.beta( 4, 2, self.N_MEMBER ) # β分布、非対称でやってみよう # 順位についての話なので、分布形状は関係ないようだ。 points.append(x_arr) # 各種目について順位を付ける for i in range( n_subj ): x_arr = points[i] n_order = x_arr.argsort() # 得点に対する順位を得る orders.append( n_order ) # 総合得点を付ける total_points = np.zeros( self.N_MEMBER ) for m in range( self.N_MEMBER ): sum = 0 for i in range( n_subj ): sum += points[i][m] total_points[m] = sum # 総合順位を付ける n_arr = np.array(total_points) total_order = n_arr.argsort() # Min(個別順位)を得る total_min = np.zeros( self.N_MEMBER ) for m in range( self.N_MEMBER ): min_order = self.N_MEMBER + 1 # 最小の順位を得る for i in range( n_subj ): if orders[i][m] < min_order: min_order = orders[i][m] total_min[m] = min_order # 出力してみよう """ for m in range( self.N_MEMBER ): row = [] for i in range( n_subj ): row.append( points[i][m] ) for i in range( n_subj ): row.append( orders[i][m] ) row.append( total_points[m] ) row.append( total_order[m] ) row.append( total_min[m] ) print( ",".join( map(str, row) ) ) """ # 総合順位 < Min(個別順位)をカウント cnt = 0 for m in range( self.N_MEMBER ): if total_order[m] < total_min[m]: cnt += 1 # 結果を返す ratio = cnt/self.N_MEMBER # print( "{}, {}, {}".format( n_subj, cnt, ratio ) ) return ratio if __name__ == '__main__': me = GeneOrder() me.run()