2018-04-10

定式化の結晶

・問題とは、何が問題なのかが分からないことが問題なのである。
・明確な質問の形にできたとき、問題は８割以上解けている。
・数学とは、解法の寄せ集めではなく、言語である。
　　　　　　　　-- 詠み人知らず。

学生の頃、先生からこんな話を聞いたことがあります。

『分析化学の仕事は、良いサンプルを準備するところまで。あとは分析機器が答を出す。』

それまで私は分析化学というものに、試薬の色が変わったとか、沈殿したとか、そんなイメージを思い描いていました。
ところがこのイメージは、現代の分析化学には当てはまりません。
分析の主役は、高度に発達した分析機器〜Ｘ線回折、ＮＭＲ、クロマトグラフィーといった一群の機械装置なのです。
もちろん試薬の色や沈殿が無くなったわけではないのですが、それらはすでに現在の主流ではありません。
数ある分析機器の中でも、私が特に驚いたのは「Ｘ線回折装置」でした。
これを使うと、タンパク質の構造はもちろん、ウィルスの構造までもが3D-CGとなってモニターに描き出されるという、まるで魔法のような機械です。
もはや“試薬の色が変わった”レベルの話ではありません。
※こんな装置です：タンパク質Ｘ線結晶構造解析
　　　 >> http://www.spring8.or.jp/ja/news_publications/research_highlights/no_05_2k/

『結晶になりさえすれば、特定できたも同然。』

確かそのようなことを、先生は口にしていたと思います。
ただ、その「結晶にする」ことがとても難しい。
難しい物質と易しい物質があるのですが、本当に知りたい物質はたいてい難しい。
簡単には結晶化しない物質もありますし、生物の中でヌルヌル動いているタンパク質を結晶化したら“死んでしまう”かもしれません。
Wikipediaには、こうありました。>> wikipedia:X線回折
『単結晶X線回折技術は三段階の基本操作から成る。
　第一段階（しばしばこれが最も難しいのだが）は測定対象物質の適切な結晶を得ることである。』

ここに至って「良いサンプルを準備する」の意味が分かってきます。
本質を損なわずに、未知なる物質を結晶として切り出すのが至難の業なのです。
なので、どんなにすごい分析機器が開発されても、分析化学の仕事は無くならないし、難しさも結局は変わりません。
ただ、分析機器が登場する以前と以後では「分析すること」の意味は大きく変わりました。

・・・あれから十数年・・・

私は分析化学に携わることはなく、代わりにソフトウェアの開発に携わってきました。
それで分析化学などもう縁が無いものと思っていたのですが、ここ最近になって、
分析化学と同じ変化が十数年のタイムラグを経て、ソフト開発の現場にやってきたように感じます。
どういうことかというと、

『ＳＥの仕事は、良い定式化を行うところまで。あとは機械が自動的に答を出す。』
『定式化さえできれば、解けたも同然。』

つまり、「結晶 -> 定式化」 ということです。

これまで私はプログラマーという仕事に、自前のアルゴリズムを工夫するとか、実装するとか、そんなイメージを抱いてきました。
ところがこのイメージは、どうやら近未来のプログラマーには当てはまらなくなりつつあります。
実際、私はＳＥという仕事に就きながら、ここ何年も自前のアルゴリズムとか、フルスクラッチ実装を（少なくとも大きな業務で）行ったことはありません。
それに代わって「定式化」の比重が圧倒的に増えました。
ソフトウェアのパッケージ化，自動化，ＡＩ化がとことん進んだ結果、システムの良否はほとんど「定式化」が負うことになったのです。
定式化とは、「現実問題を、コンピュータが扱える形に切り出すこと」です。
うまい形に切り出せれば、システムの８割は成功したも同然。
裏を返せば、難航、失敗したプロジェクトの８割は定式化が不十分だったということです。

さらに付け加えると、私の携わっている統計分析業務は、とりわけ定式化の比重が大きい分野です。
統計分析の計算そのものは、気の利いた統計解析パッケージが全自動で処理してくれます。
仕事のほとんどは、質の良い、きれいなデータを揃えることと、そもそもどんなデータを集めればよいかを考えることです。
今日の、とことん高度化した統計解析パッケージを動かすたびに、私は“Ｘ線回折装置”のことを思い起こしています。

分析化学、ソフト開発だけに限らず、「定式化」へのシフトはいずれどの分野にも押し寄せてきます。
（あるいは、もう押し寄せている。）
そしてその「定式化」の中心にあるものは、文字通り「式」なのです。
それは「解くための式」というより、まず「表現するための式」です。
ちなみに数式は英語で「Mathematical expression」、直訳すれば「数学的表現」となります。
現実問題のエッセンスを結晶化すること。
それが数式の持つパワーであり、実は数学が強烈に役立つ場面だったのです。

これは「ＯＲの４段階」として紹介されていた図です。-- 続･発想法（中公新書）より.
このように並べたとき、３つ目の「解く」は極端に言えばコンピュータが全部やってくれます。
電卓があれば筆算を行う必要はありませんが、それでも電卓のどのボタンを押すべきか、式の立て方だけは知っておく必要があります。
そうなると大事なのはむしろ「問題の定式化」「数式化」のステップなのですが、
どうも私(たち)は数学というものを「解く」ことを中心に考えるきらいがあるように思うのです。
数学とは、いかに解くか、いかにエレガントな解答を導き出すかであって、定式化、数式化のステップは、前座かオマケ程度。
たとえば学校で教わる数学の中で、文章題が占める割合はどの程度でしょうか。
たまたま私が目にした高校の教科書には、文章題はほとんどありませんでした。
ゼロかと思って尋ねてみたところ、「ここに１題あるよ」とのことだったので、１題だけ確認できました。
実際、小->中->高と進むにつれて、文章題は無くなる傾向にあります。
それだけ見ても、いかに「解く」以外がオマケ扱いか分かるでしょう。
（とってつけたような文章題が本当に「定式化」なのか、という疑問はひとまず置いておきましょう。）
それでも今後の実践を見据えるなら、いずれ「定式化」の方が「解く」以上のボトルネックになることでしょう。
そうなると「数学＝解く」のイメージがだいぶ変わってくるはずです。

イメージが変わると、何が変わるのか。
数学を必要とする人、使いこなせる人の範囲が変わります。
「解く数学」は、一握りの天才だけが必要とし、一握りの天才がいれば事足ります。
一方、「定式化の数学」は意思伝達ツールとしての性格が強く、チームメンバー全員が共有しないと意味がありません。
あるいは、共有できるような機械にＩＮＰＵＴしないと意味がありません。
また、天才だけでなく、凡人が使えないことには広がりがありません。
凡人で構わない、中身まで知る必要は無く、電卓のボタンが押せれば十分です。
ここはきれい事を並べるよりも、逆に、チームの中に１人だけ「定式化の数学」が通用しないメンバーが混じっている状況を想像してみて下さい。
その１人がどれだけ足を引っ張ることか。
特に、その１人が“無能な上司”だったりした場合には、悲惨なことになります。。。

さて、「式」が分析やシステム化に役立つのは、ある意味当然なのかもしれませんが、
これが意外な分野に役立つという話を最近耳にしました。
その意外な分野とは、「カウンセリング」です。
カウンセリングには「カウンセラーが自ら解決してはならない」という鉄則があるのだそうです。
では、カウンセラーは何をするのかというと、「ひたすら問題を整理して示す」だけです。
問題を解くのは、相談を持ちかけた本人でなければならない。
本人が解く力を身につけないことには、本当に解決したことにはならない、ということです。
新人カウンセラーがやりたくてウズウズするのだけれど、やってはいけないことは、指図すること。
つい口を突いて、ああしなさい、こうしなさいと言いたくなるのだけれど、それをグッと我慢するところが肝要なのです。
カウンセラーに相談に来る人は、ずばり解決策が聞きたくてやってくるのだけれど、
良いカウンセラーは決して直接的な解決方法を教えません。
（逆に言えば、「原因はずばり○○です」と言い切るカウンセラーは、あまり信頼できない。）
ただ、相談者がもってくる悩みを順序立てて整理し、明確な形で示すことに努める。
相談者が自ら解決できるような道筋を、ひたすらお膳立てするのだそうです。

このカウンセラーの話を聞いたとき、私は、これこそが定式化の威力だと思いました。
分析機器とコンピュータとカウンセリング。
この３つは全く別物に見えますが、定式化という側面からすれば、同じ心構えを有しています。
それは、「解く主体を全面的に信じてお任せする」ということ。
下手な自作や小細工を労するよりも、問題整理に全力を注ぎ、解くことはいっそ枯れた主体に一任する。
この定式化の方法こそが、システム化がとことん発展した現代に最もマッチしているように思えます。

2018-03-10

量子力学序説　湯川秀樹（１９４７）

亡き父の書棚を整理していたら、この古い本が見つかった。

かの湯川先生の手になる著作なのだが、着目すべきはこの本が発行された時代である。
奥付を見ると、
　昭和二十二年二月一日初版印刷
　昭和二十二年二月十五日日初版發行
とある。

終戦後間もない“お腹を空かしていた”時代に、このような量子力学の本が出回っていたこと自体に驚く。
確か仁科研の逸話だったと思うのだが、食うや食わずの状況下で、
何の腹の足しにもならない“物理学研究”に固執する日本人の姿に、ＧＨＱはむしろ呆れたと言う。
それと同じ匂いが、この本から感じ取れる。
奥付には「湯川」の検印があり、何かとてもありがたい本のような気がしてくる。

不確定性原理が記述されたページ。「ガムマ線顕微鏡」の「思考實驗」というあたりがおもしろい。

序文を見ると、原稿が完成したのは「昭和十九年十月」とある。
その後「東京の印刷所の強制疎開で組版がこはされてしまつたので出版が非常に遅れ」、
「今回改めて京都の印刷所で組み始めることと」なって、やっと出たのがこの本である。
序文の最後には「昭和二十年十二月」とあるので、正に終戦を境に作られたのだと分かる。
つまり、湯川先生は少なくとも昭和十九年までは原稿を執筆し、
印刷所は終戦の最中にあって、何とかこの本の印刷にこぎ着けたわけだ。

本の中身を見ると、カタカナ表記が少ないことに気付く。
エネルギーは「勢力」であり、Plank や Einstein は原語表記となっている。
ただし「ベクトル」「オブザーバル」などはカタカナ表記なので、カタカナが全く無いわけでもない。
また、「波動力学」と「行列力学」の対比から、一般理論に向かうという章立てが為されている。
　第二章　波動力學
　第三章　行列力學の方法
　第四章　量子力学の基礎概念
　第五章　一般理論
今、「波動力学」とはあまり言わないと思うのだが、原点に返ると、これが素直な順序のように思う。
私は長らく「なぜシュレーディンガー方程式は行列なのか？」と疑問に思っていたのだが、この順番にたどると成立過程がよく分かる。

本には「定價80.00」とあるのだが、終戦直後の100円の価値はいったいどの位なのか。

　・公務員の初任給（月給）・・・540円
　・日雇い建設労働者日給（全国平均１人１日あたり）・・・７円５０銭
　・下宿料金（月額）・・・100円
　・食パン（１斤・450g）・・・１円２０銭
　　 -- 所場代300円　現在の貨幣価値では？昭和２１年当時の物価まとめ、より。
　　 >> http://locatv.com/beppin-300yen/

この数字から察するに、少なくとも数万円は下らない高価な本だったと分かる。
もし食パンに変えれば６６斤になったわけで、ＧＨＱが呆れる気持ちも分からなくはない。

当時貧乏学生であった父は、何を思って６６斤の食パンをがまんして、酔狂にもこの本を手にしたのだろうか。
当時の時代背景と父の年齢からして、この本の内容を深く理解していたとは到底思えない。
あるいは金額からして、父の父である祖父が本代を出したのかも知れない。
それにしても“食えない高額なもの”を買ってしまった、という事情には変わりない。
ここで、量子力学とは何なのかを思い起こすと、それが「新型爆弾」の基礎であったことに思い至る。
当時の日本は「新型爆弾」を落とされて、全く意気消沈していた時代である。
そこに、量子力学という本があった。
　「日本にも、こんなすごい学門がある。」
おそらくこれが、父がこの本から唯一確実に受け取ったメッセージであり、この本の真の価値なのではないか。

ちなみに、湯川秀樹がノーベル賞を受賞したのは1949年（昭和24年）。
なので、この本はノーベル賞の直前に発行されたものである。
そう考えると、実は二年間本屋にスタックされていたものを、
ノーベル賞のニュースに浮かれてミーハーな理由で購入したのかもしれない。

さて、現在この「量子力学序説」は刊行されているのかというと、
どうやら廃版となり、古本だけが残っている状況らしい。
さらに検索したところ、理系本の収集家である“とね”さんが同じ本を持っているとブログにしたためてあった。
* 量子力学序説（湯川秀樹著）：昭和２２年初版本
>> https://blog.goo.ne.jp/ktonegaw/e/bf5b874acf0b81d58d4bf8d8e66c6adf
今後、復刊されるかどうかは分からないので、興味ある方は今のうちに古本を探してみるとよいだろう。

2018-03-02

運動エネルギー、指数分布、正規分布

[１]．なぜ運動エネルギーは速度の２乗なのか。
[２]．なぜエネルギーを無作為に分配すると、指数分布（ボルツマン分布）となるのか。
[３]．なぜ独立した試行を足し合わせると、正規分布となるのか。

一見何の関係も無さそうに見えるこの３つは、実は共通の思想から生み出されている。
３つ並べると、そこに見えてくるものがある。

[１]．なぜ運動エネルギーは速度の２乗なのか。

前提：
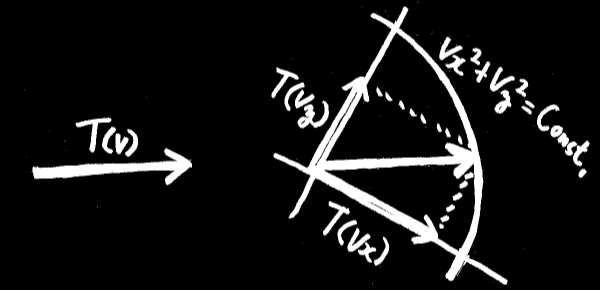
(1) 速度とはベクトル〜長さと向きを持った矢印で表される。
(2) 運動エネルギーとは、速度の向きに依存せず、大きさだけに依存するスカラー量（１個の数字で示される量）のことである。
(3) 空間とは一様に平ら（ユークリッド的）で、ベクトルは縦横に分解・合成できる。

とある速度ベクトルを別の角度から見ても、運動エネルギーは変わらない。
つまり、

この左右２つが等しくなければならない。
であれば、運動エネルギー T(v) = A v^2 以外にあり得ない。
　　※ なぜなら、ベクトルで円を描いた軌跡は vx^2 + vy^2 = r^2 = Const. だから。
　　※ また、求める関数は線形である必要がある。T(vx + vy) = T(vx) + T(vy).
　　※ この線形性から、求める関数は v２乗の１次式でなければならない。
この係数 A の半分のことを、我々は「質量」と呼んでいる。すなわち A = m/2 。
さらに、T(v) = (m/2) v^2 + C のように、ある一定の定数を付け加えても理論上は成り立つ。
通常、我々はこの定数の反対符合のことを「位置エネルギー」と呼んでいる。すなわち C = - U 。
位置エネルギー U は、一般的には場所ごとに異なる値を持っていてもかまわない。
つまり U は位置 q の関数 U(q) である。
　　※ あるいは空間の一様性を前提としたので(3)、場所ごとの違いを明示的に U(q) で示した、とも言える。

ここで「力」を「位置の違いによってエネルギー変化をもたらすベクトル」であると定義するならば、次のように書ける。

　F = ∂(T - U) /∂q
　　　(Tは運動エネルギー、Uは位置エネルギー、q は一般化座標)

力とは、運動エネルギー、位置エネルギーの別によらず「とにかくエネルギーの差分があるところに生じるベクトル」だと解釈できる。
実はここに、なぜ U にプラス符合ではなく、マイナス符合を付けたかの理由がある。
位置エネルギーが高くなるほど、坂を上るほど「反対の下り坂の向きに力を受ける」とするのが自然だから。

物体を動かす力の元になるエネルギー要因を、一定時間に渡って合計した値を「作用(action)」という。
力の元になるエネルギー要因 (T - U) は「ラグランジアン」と名付けられている。
ラグランジアンを用いて、作用 S は次のように書ける。

　S = ∫(T - U) dt

あらゆる物体は、作用を最も小さく（停留化）するように振る舞う。
これを「最小作用の原理」と言う。
最小作用の原理に、それ以上の「なぜ」は無い。
なぜかは説明できないけれど、原理として受け入れると全てが上手く行く。
実はたったこれだけで、古典力学の“全て”が構成できるのだ！
（詳しくは「ランダウ=リフシッツ理論物理学教程　力学」を参照のこと。）

[２]．なぜエネルギーを無作為に分配すると、指数分布（ボルツマン分布）となるのか。

前提：
(1) 確率の積の法則：
　　確率 Pa で生じる事象と、確率 Pb で生じる事象が、合わせて同時に起こる確率は Pa・Pb という確率の積になる。
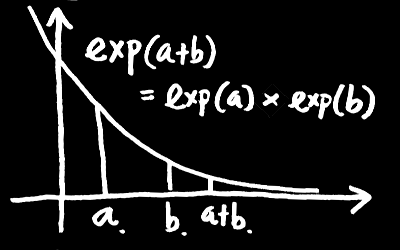
(2) 指数関数 exp(x) とは、足し算を掛け算に直す関数のことである。
　　　exp(a + b) = exp(a)・exp(b)
　　底の違いや定数倍を除いて、足し算を掛け算に直す（連続的で自然な）関数は指数関数だけである。

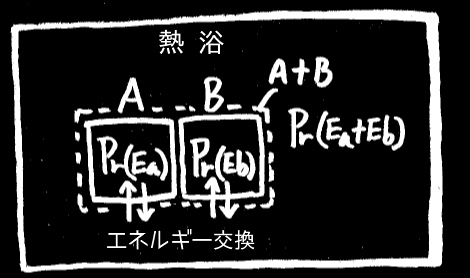
一定のエネルギーに満ちた（一定温度下にある）十分大きな熱浴環境を考える。
この環境の中で、熱浴とエネルギーをやり取りしている、とある一部分がエネルギー E を持つ確率分布 Pr を知りたい。
ある部分 A が、エネルギー Ea だけ持っている確率を Pr(Ea) としよう。
別の部分 B が、エネルギー Eb だけ持っている確率を Pr(Eb) としよう。
そして A と B には何ら特別な違いはなく、Pr はどの部分をとっても均質だったとしよう。
２つの部分を合わせた a+b 全体がエネルギー Ea+Eb を持つ確率は、確率の積の法則から、
　　Pr(Ea + Eb) = Pr(Ea)・Pr(Eb)。
これは、足し算を掛け算に直す関数なので、指数関数である。

もしこれが理想気体であったなら、個々の分子が持つ運動エネルギーの総和を
（さしあたり位置エネルギーは無視できるものとして）指数関数に従って分配すれば、
分子１個あたりが持つエネルギーの確率が導き出せる。
あらゆる化学反応は（レーザーか何かで局所的に特殊な分布でも作り出さない限り）、
このエネルギー分布に従って進行する。

あるいは、閉じた社会の中で均質な人々が一定量のお金を交換し合ったなら、
１人が持つお金の確率は（他に何の要因も無ければ）指数分布に従って分配されることになる。
（きっと社会における“化学反応”も、お金の分布に従って進行している。）

[３]．なぜ独立した試行を足し合わせると、正規分布となるのか。
　上記、[１] と [２] を合わせると、[３] が導き出される。

前提：
(1) 正規分布の骨格は、
　　N(x) = C exp( - A x^2 )

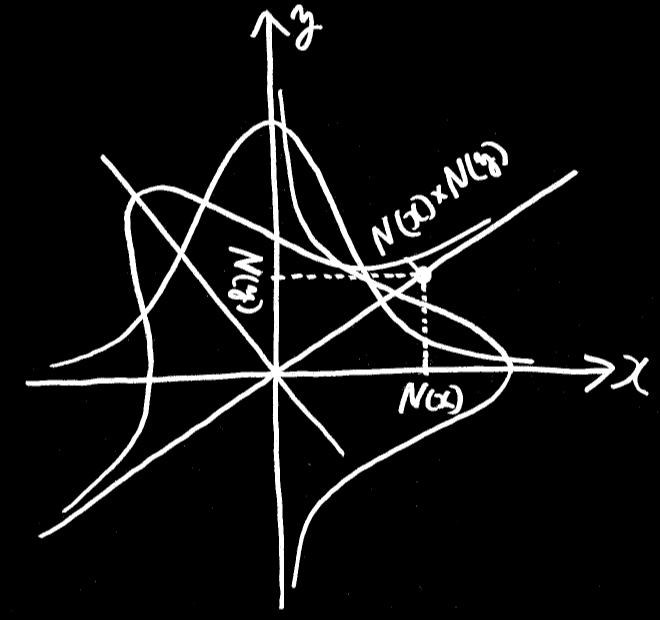
平面の的にボールを当てることを考えたとき、ボールが中心から外れる誤差の分布 N( r^2 ) の形状を知りたい。
誤差はあらゆる方向に対して独立なので、
　横方向 x の誤差は、N( x^2 )、
　縦方向 y の誤差は、N( y^2 )、
　縦横合わせた誤差は、N( x^2 )・N( y^2 )　　　<- 確率の積の法則.

的の中心からボールが当たった点までの距離の２乗は x^2 + y^2 だから、
　　N( x^2 + y^2 ) = N( x^2 )・N( y^2 )
これは、足し算を掛け算に直すのだから、指数関数である。
つまり、独立した誤差を合わせた確率分布は、
　　N(x) = exp( a x^2 )
の骨格を持つ。
係数 a がプラスでは成り立たない（発散する）ので、結局のところ正規分布は
　　N(x) = C exp( - A x^2 )
となる。
　 * 正規分布の導出 >> d:id:rikunora:20170310

正規分布が、あらゆる統計の基礎であることは言を俟たないであろう。

以上、３つの「なぜ」、力学、統計力学、統計学が、全て共通の思想から出ていることが読み取れただろうか。
あえて言葉で記すなら、
　『同一の実体を異なる視点から捉えれば、実体の普遍性から、視点を規定する法則が生じる』
とでも表現できようか。
　[１]．違う角度から見ても同一の実体がエネルギー。
　[２]．全体と部分で整合性がとれるのが、実現する確率分布。
　[３]．違う角度から見て、独立した試行の整合性がとれるのが、最も自然な確率分布。

あるいはネーターの定理に見る「対称性が保存則を導く」であるとか、
現代物理の基本要請である「ローレンツ不変」なども、同じ思想の所産だと思う。
これらについては徒に言葉をもてあそぶより、上記３つの核心にあるものを、じっくり鑑賞してほしい。

2017-12-10

コーシー分布とarctan微分

目隠しをしたアーチェリー選手が、長い壁に向かってランダムにたくさんの矢を放ったら、矢の当たった点はどのような分布に従うか。
答は「コーシー分布」(Cauchy distribution) になります。
コーシー分布は、よく知られている正規分布とは、似たようなベル型カーブであってもかなり性質が異なります。
特に際だった性質は、“平均も分散も無い”ということ。
たとえ１本であっても、うんと遠くに矢が当たったなら、それに引っ張られて平均が安定しないということです。
* そんなの常識、あたりまえでない大数の法則 >> http://miku.motion.ne.jp/stories/08_LargeNum.html

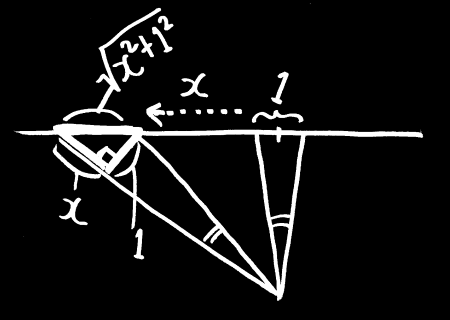
この図から、コーシー分布がどんな数式で表されるか、考えてみましょう。
矢の角度θを動かしたとき、矢のあたる場所は tan(θ) となります（定数は省略）。
矢の当たった数、つまり当たった点の密度は、tan(θ) のグラフの曲線の変化が大きいところほど濃くなります。
tan(θ) のグラフの曲線を横から見たものは tanの逆関数 arctan(θ) ですから、
当たった点の密度は arctan(θ) の変化、すなわち arctan(θ) の微分ということになります。
arctan の微分はどうなるか。
WolframAlpha (https://www.wolframalpha.com/) という計算サイトに行って、
「arctan(x)'」と入力すると、以下の答が得られます。

　 (d/dx) arctan(x) = 1 / (x^2 + 1)　　・・・これがコーシー分布の実質的な骨格です。

この arctanの微分の意味を、アーチェリーから問い直してみましょう。
まず、矢の代わりにサーチライトで長い壁を照らすことを考えます。

壁の正面を照らしたとき、サーチライトのスポットの大きさが１だったとましょう。
正面から x だけ離れた位置をサーチライトで照らしたなら、スポットの大きさはピタゴラスの定理から √(x^2+1)だけ大きくなります。
今考えたサーチライトでは、距離が x だけ離れた様子を想定しましたが、
アーチェリーの場合は距離ではなく、角度が変動の元になっていました。
この距離と角度の関係を表したのが次の図です。

ある一定の角度が、正面の長さの１に対応していたとき、
x だけ離れた場所で対応する長さは、やはりピタゴラスの定理から √(x^2+1)となります。

コーシー分布＝「角度の変化に対する、矢が当たった点の密度の変化」は、上記、
　１．サーチライトのスポットの大きさ -- 密度そのものの変化
　２．長さと角度の対応関係
の２つを掛け合わせた値に反比例するので、結局
　　コーシー分布＝ 1 / { √(x^2+1) * √(x^2+1) } = 1 / (x^2+1)
となります。
なぜ反比例なのかというと、スポットが長くなればなるほど、密度は薄くなるから。

「目隠しされたアーチェリー選手」のたとえは、「禁断の市場（マンデルブロ著）」という本から引用したものです。
マンデルブロは、市場の変動は正規分布のように安定したものではなく、
むしろコーシー分布に近い“平均も分散も無い”世界なのだと主張しています。

禁断の市場フラクタルでみるリスクとリターン

作者: ベノワ・B・マンデルブロ,リチャード・L・ハドソン,高安秀樹,雨宮絵理,高安美佐子,冨永義治,山崎和子
出版社/メーカー: 東洋経済新報社
発売日: 2008/06/06
メディア: 単行本
購入: 9人クリック: 91回
この商品を含むブログ (32件) を見る

ところで、正規分布とはどのようなものであったかと言うと、
　「平面の的を目がけてボールを当てたとき、中心からのずれの大きさの分布」
ということでした。
* 正規分布の導出 >> [id:rikunora:20170310]
ということは、ボールだと正規分布で、矢だとコーシー分布なのか？
両者の違いは、ボールは距離（長さ）で測っているが、矢は角度で測っている、という点にあります。
正規分布の“長さ”で行っていた議論を、そっくりそのまま“角度”に置き換えようとしても、うまく行きません。
的の中心から、横方向に長さ x、縦方向に長さ y ずれた点にボールが当たる確率は x^2+y^2 と表せるのですが、
横方向に角度 θ、縦方向に角度 φ ずれた点に矢が当たる確率は、θとφの何らかの和にはなりません。
２つの分布の違いは結局のところ、測り方の違いに求められると思うのです。

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
久々にブログ更新しました。
ここ最近雑事が多く、ブログを書くゆとりがありません。
頂いたコメントなど、ろくに返事もできず、すいません。

2017-10-22

4つの数字で10を作る

４つの数字と＋−×÷を使って１０を作るパズルを解くプログラム。
切符の数字や、自動車のナンバープレートの数字などで、きっとやったことがあると思う。

プログラムの考え方は単純で、コンピュータの力にあかせて全ての組み合わせを試してみる、というもの。

・２個の数字から＋−×÷で作ることができる全部の数字を列挙する。
・それを使って、３個の数字から作ることができる全部の２個の数字を列挙する。
・それらを使って、４個の数字から作り出すことができる３個の数字を列挙する。
・４個の数字は 3:1 に分ける場合と、2:2 に分ける場合があるので、両方とも試す。
・４個の数字は 0000 〜 9999 だから、たかだか１万通り全部試してみればいい。

ソースコードを文末に貼り付けておきました。phpという言語で書いてあります。

さて、なぜ唐突に１０を作る問題を取り上げたかというと、ここ最近囲碁とブログにはまっているrikunora妻が、
ある日、難しいパズルが解けたと言って、この問題を持ちかけてきたからです。
* １０を作る　まだ言ってる >> https://ameblo.jp/rikunora/entry-12321427106.html
* そんなのググれば… >> https://ameblo.jp/rikunora/entry-12321424248.html
* 3478 >> https://ameblo.jp/rikunora/entry-12321077566.html

『( 3, 4, 7, 8 ) を使って 10 を作れ。』
この答、コンピュータの力を借りずに自力で解くのは、かなり難しい。
自分の頭で解くことは早々にあきらめ、プログラムを走らせると、以下の出力が得られます。

( 3, 4, 7, 8 )
3 4 7 8
1.75 3 8
1.25 8
10
OK

この数字の列を上から読み解いて、
　( 3 - 7 / 4 ) * 8 = 10
という解答が得られるわけです。
あっさり解けたように見えますが、コンピュータの力を借りず自分の頭で解くのはかなり大変だったはずで、
rikunora妻には一定の評価を与えないわけにはいきません。

この 10を作るプログラム、元をたどれば今を去る数十年前、まだ rikunora がプログラムというものを覚え立ての頃、
8-bitマイコン上の N-BASICで作った記憶があります。
当時、上のやり方を友人から教わり、かなり苦労して作ったあげく、
プログラムを１晩以上ぶっ続けで回し続けてようやく結果が得られたものでした。
今は同じ事がちょっとした合間にできて、答も一瞬にして求まるという、長足の進歩ですねぇ。（おっさんの昔話）

<?php
/**
* ４個の数字から＋−×÷を用いて１０を作る問題
*/
class	Make10 {

	protected	$Input = array( 0, 0, 0, 0 );	// 入力する４個の数字
	protected	$FinalAns = 10;		// 最後に期待する答、デフォルト=10
	protected	$IsSolved = false;	// 解けたかどうかフラグ、１パターンで探索を打ち切るときに使う
	protected	$TraceStack = array();	// 途中経過を表示するためのスタック
	
	////////////////////////////////////////////////////////////////////
	
	/**
	* ４つの数字を配列にして入力する
	*/
	public function setInput( array $input0 ){
		$this->Input = $input0;
	}
	
	/**
	* 期待する答をセットする、デフォルト値=10
	*/
	public function setFinalAns( $ans ){
		$this->FinalAns = $ans;
	}
	
	/**
	* 処理実行
	*/
	public function run(){
		$this->IsSolved = false;
		$this->TraceStack = array();
		
		$this->resolve( $this->Input );
		
		return $this->IsSolved;
	}
	
	////////////////////////////////////////////////////////////////////
	
	/**
	* 計算処理の中心部
	* 扱っている数字の個数（０〜４個）によって再帰的に処理を行う
	*/
	protected function	resolve( array $numbers ){
		
	//	if( $this->IsSolved ){	// １回解けたら打ち切る
	//		return;
	//	}	// このさい全パターンやってみよう
		
		// 結果表示のため、今、試している数字の組を積んでゆく
		array_push( $this->TraceStack, $numbers );
		
		switch( count($numbers) ){	// 数字の個数で場合分け
			case 1:
				$result = $this->oneNumber( $numbers );
				if( $result ){
					$this->printStack();	// 途中経過を出力
					$this->IsSolved = true;	// 解けた！
				}
				break;
			
			case 2:	// 数字が２個
				$result = $this->twoNumbers( $numbers );
				foreach( $result as $ans ){
					$this->resolve( $ans );	// 再帰呼び出し
				}
				break;
			
			case 3:	// 数字が３個
				$result = $this->threeNumbers( $numbers );
				foreach( $result as $ans ){
					$this->resolve( $ans );	// 再帰呼び出し
				}
				break;
				
			case 4:	// 数字が４個
				$result = $this->fourNumbers( $numbers );
				foreach( $result as $ans ){
					$this->resolve( $ans );	// 再帰呼び出し
				}
				break;
			
			default:
				print "ERROR: 意図しない数字の個数、". count($numbers) ."個.\n";
				exit();
		}
		
		array_pop( $this->TraceStack );
	}
	
	/**
	* スタックの表示
	*/
	protected function printStack(){
		foreach( $this->TraceStack as $numbers ){
			print "\t";
			foreach( $numbers as $num ){
				print "$num ";
			}
			print "\n";
		}
	}
	
	const EPS = 0.00000001;	// 判定誤差
	
	/**
	* １個の数字の処理
	* 解けたかどうかの判定
	*/
	protected function oneNumber( array $numbers ){
		$result = false;
		
		$a = $numbers[0];
		
		// 探していた答と一致するか判定
	//	if( $a == $this->FinalAns ){	// 誤差を考慮に入れる
		if( ($a - $this->FinalAns) < self::EPS
		 && ($a - $this->FinalAns) > - self::EPS ){
			$result = true;
		}
		
		return $result;
	}
	
	/**
	* ２個の数字の処理
	* ２個の数字が作り出すことのできる全ての１個の数字を返す
	*/
	protected function twoNumbers( array $numbers ){
		$result = array();
		
		$a = $numbers[0];
		$b = $numbers[1];
		
		$ans = $a + $b;	 $result[0] = array( $ans );
		$ans = $a - $b;	 $result[1] = array( $ans );
		$ans = $b - $a;	 $result[2] = array( $ans );	// 引くには逆順がある
		$ans = $a * $b;	 $result[3] = array( $ans );
		if( $b != 0 ){	// 0割禁止
			$ans = $a / $b;	 $result[4] = array( $ans );
		}
		if( $a != 0 ){	// 0割禁止
			$ans = $b / $a;	 $result[5] = array( $ans );	// 割るには逆順がある
		}
		return $result;
	}

	/**
	* ３個の数字の処理
	* ３個の数字が作り出すことのできる全ての２個の数字の組を返す
	*/
	protected function threeNumbers( array $numbers ){
		$result = array();
		
		$a = $numbers[0];
		$b = $numbers[1];
		$c = $numbers[2];
		
		// (ab)c, (bc)a, (ca)b の３通りの組み合わせ
		$idx = 0;
		
	//	print "Try3: $a, $b, $c \n";
		$result3 = $this->threeOrders( $a, $b, $c );
		foreach( $result3 as $ans ){
			$result[$idx] = $ans;
			$idx++;
		}
	//	print "Try3: $b, $c, $a \n";
		$result3 = $this->threeOrders( $b, $c, $a );
		foreach( $result3 as $ans ){
			$result[$idx] = $ans;
			$idx++;
		}
	//	print "Try3: $c, $a, $b \n";
		$result3 = $this->threeOrders( $c, $a, $b );
		foreach( $result3 as $ans ){
			$result[$idx] = $ans;
			$idx++;
		}
		
		return $result;
	}
	
	/**
	* ３個の数字を(2個,1個)に分けて、２個の数字の組を返す
	*/
	protected function threeOrders( $a, $b, $c ){
		$result = array();
		
		$result2 = $this->twoNumbers( array( $a, $b ) );
		
		$idx = 0;
		foreach( $result2 as $ans ){
			$result[$idx] = array( $ans[0], $c );
			$idx++;
		}
		
		return $result;
	}

	/**
	* ４個の数字の処理
	* ４個の数字が作り出すことのできる全ての３個の数字の組を返す
	*/
	protected function fourNumbers( array $numbers ){
		$result = array();
		
		$a = $numbers[0];
		$b = $numbers[1];
		$c = $numbers[2];
		$d = $numbers[3];
		
		// ３：１の組に分ける、(abc)d, (bcd)a, (cda)b, (dab)c
	//	print "Try4-31: $a, $b, $c, $d \n";
		$result += $this->fourOrders31( $a, $b, $c, $d );
		
	//	print "Try4-31: $b, $c, $d, $a \n";
		$result += $this->fourOrders31( $b, $c, $d, $a );
		
	//	print "Try4-31: $c, $d, $a, $b \n";
		$result += $this->fourOrders31( $c, $d, $a, $b );
		
	//	print "Try4-31: $d, $a, $b, $c \n";
		$result += $this->fourOrders31( $d, $a, $b, $c );

		// ２：２の組に分ける、(ab)(cd), (ac)(bd)
	//	print "Try4-22: $d, $a, $b, $c \n";
		$result += $this->fourOrders22( $a, $b, $c, $d );
		
	//	print "Try4-22: $a, $c, $b, $d \n";
		$result += $this->fourOrders22( $a, $c, $b, $d );

		return $result;
	}

	/**
	* ４個の数字を(3個,1個)に分けて、３個の数字の組を返す
	*/
	protected function fourOrders31( $a, $b, $c, $d ){
		$result = array();
		
		$result2 = $this->threeNumbers( array( $a, $b, $c) );
		
		$idx = 0;
		foreach( $result2 as $ans ){
			$result[$idx] = array_merge( $ans, array($d) );
			$idx++;
		}
		
		return $result;
	}

	/**
	* ４個の数字を(2個,2個)に分けて、２個の数字の組を返す
	*/
	protected function fourOrders22( $a, $b, $c, $d ){
		$result = array();
		
		$result2A = $this->twoNumbers( array( $a, $b ) );
		$result2B = $this->twoNumbers( array( $c, $d ) );
		
		$idx = 0;
		foreach( $result2A as $ansA ){
			foreach( $result2B as $ansB ){
				$result[$idx] = array_merge( $ansA, $ansB );
			}
		}
		
		return $result;
	}
}

////////////////////////////////////////////////////////////////////////
// BEGIN Main

$self = new Make10();
$self->setFinalAns( 10 );

/* 特定の数字の組で試す *
$self->setInput( array( 9, 9, 9, 9 ) );
if( true == $self->run() ){
	print "OK";
}
/* */

/* 0〜9999 まで全てを試す */
for( $n=0; $n <=9999; $n++ ){

	$m = $n;
	$a = floor($m / 1000);
	$m -= ($a * 1000);
	$b = floor($m / 100);
	$m -= ($b * 100);
	$c = floor($m / 10);
	$m -= ($c * 10);
	$d = $m;

	print "( $a, $b, $c, $d )\n";

	$self->setInput( array( $a, $b, $c, $d ) );
	if( true == $self->run() ){
		print "OK";
	}
	print "\n";
}
/* */

?>

2017-10-22

自民と希望の政策キーワードを可視化してみた

今日の衆議院選挙の参考に、自民党と希望の党の政策テキストを２次元マップに可視化してみた。
詳しい方法は後に回すとして、まずは結果から。

● 自民党、全体。中心はごちゃごちゃしてよく分からないが、「農業」とか「革命」などが意味的に突出しているようだ。

● 自民党、ごちゃごちゃを拡大。なんとなく重要キーワードが群を成している。

● 自民党、さらに拡大。

個人的に気になる、「IoT, ICT」といったキーワードは、「加速、活躍、所得」に近いらしい。
一方、「税」は「削減、適切」に、「データ」は「外国、着実、総合」に近いのだろうか。

● 希望の党、全体。こちらでは「政府, 検討」などが大きく外れている。

● 希望の党、ごちゃごちゃを拡大。

● 希望の党、さらに拡大。

こちらでは「EV, ユリノミクス, エネルギー」といったキーワードが目立つ。
眺めていると、どことなく自民党と集まり方が違う。

試しに両方の党で、「日本」「原発」といったキーワードに近い単語を出力すると、こんな感じに。

● 自民党
・CHECK_WORD= 日本
1. 事案 0.8811548352241516
2. 紛争 0.869037389755249
3. 則る 0.8689562678337097
4. 出す 0.8679717779159546
5. サイクル 0.8678414821624756
6. ハブ 0.8675268888473511
7. 仲裁 0.8667996525764465
8. 結論 0.8663533926010132
9. 額 0.865086019039154
10. 柱 0.863643229007721
・CHECK_WORD= 原発
1. 区域 0.9755296111106873
2. 暮らし 0.9720321893692017
3. 総務 0.9708766937255859
4. 支払 0.9689890742301941
5. 省 0.9675025939941406
6. 統合 0.9669897556304932
7. 直接 0.9648252129554749
8. ほとんど 0.9646211862564087
9. 除く 0.9640038013458252
10. 方針 0.9639186859130859

● 希望の党
・CHECK_WORD= 日本
1. 満たす 0.9634389877319336
2. 率 0.9588447213172913
3. 都市 0.9553815126419067
4. 踏まえる 0.9451758861541748
5. 水産 0.9422210454940796
6. 徹底 0.9415571093559265
7. 近海 0.9351164102554321
8. 他国 0.9350647926330566
9. ガイドライン 0.930781364440918
10. 道路 0.9273162484169006
・CHECK_WORD= 原発
1. 老朽 0.9683917760848999
2. 方針 0.9643222689628601
3. 額 0.9633558988571167
4. 経験 0.9626327753067017
5. 公費 0.9625997543334961
6. 総合 0.9602236747741699
7. 以上 0.9596429467201233
8. 20 0.9584065079689026
9. 40 0.9578380584716797
10. 補てん 0.955456018447876

■ 方法

(1). 各党のホームページから、政策が書かれたテキストを取得した。
・自民党: 衆議院選挙公約2017, 政策BANK >> https://special.jimin.jp/political_promise/bank/
・希望の党: 政策について >> https://kibounotou.jp/policy/

(2). 各テキストを、Pythonの分かち書き"janome"を用いて単語に分解した。
日本語形態素解析器"janome" >> http://mocobeta.github.io/janome/
分かち書きの際、['助詞', '助動詞', '記号'] は除外し、活用のある単語は原型とした。以下のような感じ。

* 自民党テキスト

Ⅰ . 経済再生
生産性革命
少子高齢化最大壁立ち向かうため生産性革命人づくり革命断行するこの 2 大改革新しい経済政策パッケージ年内取りまとめる
ロボット IoT 人工知能 AI 生産性劇的押し上げる最先端イノベーション起こす生産性革命実現する
2020 年 3 年間生産性革命集中投資期間大胆税制予算規制改革あらゆる施策総動員する
人手不足高齢化補うためロボット IoT 人工知能 AI 企業生産性飛躍的高める投資推進する特に生産性低い業種中堅企業中小企業小規模事業者集中的支援する

* 希望の党テキスト

政策集私たち目指す希望道
１政治希望　〜徹底する情報公開透明性高い政治実現〜
特区等事業者選定その選定過程国民全て開示する
企業団体献金ゼロ法的義務付ける
地方議員政務活動費公開同様国会議員文書通信交通滞在費使途公開義務付ける
衆議院参議院対等統合一院制迅速意思決定可能する議員定数議員報酬国会運営費用大幅削減する

(3). Python の gensim, word2vec を用いて、取り出した単語をベクトル化した。
分かち書きしたテキストを、以下のようなコードに放り込むだけ。

from gensim.models import word2vec

sentences = word2vec.LineSentence( INPUT_FILE )
model = word2vec.Word2Vec(sentences,
                          sg=1,
                          size=100,
                          min_count=1,
                          window=10,
                          hs=1,
                          negative=0 )
model.save( OUTPUT_FILE )

(4). できあがった word2vecモデルを t-SNEという方法で２次元に圧縮し、プロットした。
# 参考: gensimのword2vecの結果を手軽に可視化する方法 >> https://hacknote.jp/archives/25247/

import numpy as np
from gensim.models import word2vec
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt 
from matplotlib.font_manager import FontProperties

# word2vecで作成したモデルのファイル名
#INPUT_MODEL = "w2v_jimin.model"
INPUT_MODEL = "w2v_kibo.model"

#vocab_thresh   = 7    # 自民の場合、７回以上登場する単語を拾う、258単語だった
vocab_thresh = 3    # 希望の場合、３回以上登場する単語を拾う、197単語だった

if __name__ == "__main__" :
    
    word2vec_model = word2vec.Word2Vec.load( INPUT_MODEL )

    # 単語の一覧を取得する
    vocabs = []
    for word, vocab_obj in word2vec_model.wv.vocab.items():
        if vocab_obj.count >= vocab_thresh:    # N回以上登場する閾値
            vocabs.append( word )
    
    n_vocab = len(vocabs)
    print( u"単語数={}", n_vocab )
    
    emb_tuple = tuple([word2vec_model[v] for v in vocabs])
    X = np.vstack(emb_tuple)
    
    model = TSNE(n_components=2, random_state=0)
    np.set_printoptions(suppress=True)
    model.fit_transform(X) 
    
    # matplotlibで t-SNEの図を描く
    skip = 0
    limit = n_vocab  # 全単語を出力しよう
    
    # 日本語フォント対応、Windowsの場合
    fp = FontProperties(fname=r'C:\WINDOWS\Fonts\YuGothB.ttc', size=14)
    
    plt.figure( figsize=(40,40) )
    plt.scatter( model.embedding_[skip:limit, 0], model.embedding_[skip:limit, 1] )
    
    count = 0
    for label, x, y in zip(vocabs, model.embedding_[:, 0], model.embedding_[:, 1]):
        count +=1
        if( count < skip ): continue
        plt.annotate(label, xy=(x, y), xytext=(0, 0), textcoords='offset points', fontproperties=fp)
        if( count == limit ): break
    
    plt.show()

こうして出来たのが、最初に挙げたテキストマップというわけ。

2017-10-14

東京→大阪(諏訪湖経由)自転車24時間“中山道キャノンボール”達成！

自転車

東京の日本橋, 国道１号起点から、大阪の梅田新道, 国道１号終点まで、
甲州街道、諏訪湖、中山道経由、552kmを自転車で 24時間以内に走破した。
５回目のチャレンジ（東海道まで含めれば８回目のチャレンジ）にしてようやくの達成。
これまでの苦労が全て報われた、最高の気分だ。自転車に乗り続けてきてよかった！

　　2017/10/08(土) AM 04:50 〜 10/09(日) AM 03:47
　　距離: 552.48km　　　累積上昇高度: 4,552m (GPS-Watchログによる)
　　タイム: 22時間 47分 27秒　　　平均時速: 24.15km

体調、天候、交通量、運、全てがそろって上手くいった。
アクシデント、トラブル、パンクは一切無し。ハンガーノックも胃弱もほとんど無し。
同じことは、もう二度とできないだろうと思う。

■ これまでの記録

第１回：中山道キャノンボールは長かった >> [id:rikunora:20160510]
　　2016/05/01〜02　　28時間 33分 32秒
第２回：中山道キャノボ成らず、遙かなり大阪 >> [id:rikunora:20161025]
　　2016/10/10　　チェーン切れ、名古屋、小牧にてリタイア
第３回：逆方向の大阪->木曽->東京　（ブログに記載無し）
　　2016/11/30〜31
　　夜の寒さに断念、約３０時間で東京到着
第４回：中山道キャノンボールあと１時間 >> [id:rikunora:20170520]
　　2017/05/01〜02　　24時間 56分 07秒

さらに、それ以前の東海道キャノンボールの記録。

* 東京→大阪24時間自転車走破“キャノンボール”達成！ >> [id:rikunora:20141006]

■ ルートラボの記録
* 中仙道キャンボール達成(前半) >> https://yahoo.jp/FXx9zCH
* 中仙道キャンボール達成(後半) >> https://yahoo.jp/vGb2r2

■ 行程表
当初に立てた計画表と、実際の走行タイム。

一宮まで平均25kmを維持、一定ペースで貯金タイムを稼ぎ続けた。それ以降も大幅ペースダウンはしていない。
最もきつかった０時付近の睡魔も、問題なくやり過ごした。

途中休憩は７回、うちコンビニ補給は１回（木曽福島にて）。
おにぎりとウィダーインゼリーは、基本、走りつつ食べた。

（サイコンの記録とGPS-Watchの記録にずれがあるのは、サイコンのGPS補足が遅れてスタートしたから。）

■ 天候
晴れ〜薄曇り。昼は22℃、夜は19℃。全体を通じてほぼ無風。理想的な天気に恵まれた。
過去に苦しめられた、山間部での向かい風や、関ヶ原以降の急な気温低下などが、今回は全く無かった。

この前日まで雨、翌日は極端な暑さだったので、この日だけがピンポイントで好条件だったわけだ。

■ 自転車
・TIME VX Elite
　　ひと言で言えば、最高！
　　剛性の低い”柔らかめ”のフレームなのだろうか、とにかく足に疲れがこない。
　　高速をソツなくこなす。不思議と“スピード感”が無い。
　　たとえば木曽高速の下りで、気がついたら 50km出ていた、
　　といった具合に、メーターを見て思ったよりも速かったことに驚かされる。

・DURA-ACE 7800
　　これも最高！
　　ギア比: フロント 50x40、リア 11〜28（スプロケットはアルテグラ）
　　前回はノーマルスプロケット 12〜25を用いていたのだが、今回ワイドレシオにしたのが正解だった。
　　中仙道は山あり谷あり平地ありなのだから、やはり幅広く対応できる方が良い。
　　（東海道キャノンボールを達成したときもワイドレシオだった。）

・Ksyrium SLS + Continental GrandPrix TT
　　いくつかの車輪を試してみたところ、結局キシリウムが一番相性が良かった。
　　よく「キシリウムは固い」と言われるのだが、フレームが柔らかいためか、組み合わせバランスはこれがベスト。
　　今回はじめて GrandPrix TT というタイヤを使ったところ、これが実に良かった。
　　まるでキャノンボールのためにあるタイヤだ。私の評価では過去最高。
　　私を含め多くのライダーが GP4000s2 を使っているかと思うのだが、
　　この GrandPrix TT は、GP4000s2 をさらに軽く、しなやかにした感じだ。
　　最初に乗った瞬間「おっ、これは！」と思った。
　　気になる点は耐久性だが、とにかく今回ノーパンクだったので、信頼を得た。
　　チューブには軽量チューブ（R-Airなど）を避け、ノーマルチューブを用いた。
　　軽量チューブは確かに投資の割に走りが改善されるのだが、
　　過去の経験からすると、どうも軽量チューブの方がわずかにパンクの確率が上がるように思える。
　　キャノンボールではパンクは絶対に避けたいので、安全を見てノーマルチューブとした。

・ハンドル: NITTO Mod55
　　昔からある定番ハンドル、手にしっくりくる。
・Profile T2 DL -- ショートエアロバー
　　ハンドルを握る箇所が１つ増えるので疲労低減に有効。
　　平地で前乗りすると、かなりのスピード維持ができる。
・シマノプロバーテープスポーツコンフォート
　　手が痛くなる対策に、とにかく厚手でフカフカのバーテープを使った。

・サドル: サンマルコロールスチタンミエレ
　　昔からあるクラシカルなサドルで、私の大のお気に入り。座り心地は抜群で 500km越えにも耐えられる。
・シートポスト: 3T DORICO TEAM
　　サドルの位置を満足行くまで合わせるため、昨年からシートポストを２回変えた。
　　最終的にセットバックが大きく取れる、このシートポストに落ち着いた。
　　特に長い上り坂では「後乗りでクルクル回すスタイル」が取れるようになった。

・ペダル: Mavic Zxellium SLR
　　要はTimeと同じもの。

* 電装系：
・フロントライト: Volt300ｘ２本。
　　Volt400のバッテリーを付けると長持ちする。主にミドルモードで使用した。
・リアライト: CatEye RAPID 3
・Dixna ドロップエンドライト
　　バーエンドに取り付ける後方用ライト。特にトンネルで、とっさに点灯したいときに役立つ。
・ヘルメットに取り付けるライト: Topeak Headlux
　　前方に白色、後方に赤色に点滅する小型のライト。とにかく目立つように。

■ 服装

天気予報で気温が高めになると予想されたので、薄手の服装を選んだ。
・ベースレイヤー: ASICS ランニング用長袖シャツ
・ろんぐらいだぁすサイクルジャージ
　　東海道キャノンボール達成時、青森ロングライド達成時に着ていたジャージ。今回も験を担いで。
・手袋は２重。薄手のレーシング用手袋＋古くなって伸びたパッド入り手袋

・CRAFT蛍光ウィンドブレーカー、夜間に着用。
・パールイズミレーサータイツ
・あと、夜間の気温低下に備え、上着＋メットカバーを携行したのだが、今回は出番が無かった。

■ 携行品
今回はフレームバックとサドルバックを装備し、体には一切荷物を付けなかった。
　・APIDURA フレームバッグスモールサイズ
　・FAIRWEATHER サドルバッグ Mini (TOKYO Wheels限定カラー・ネイビー)
この２つのバッグは傑作と言ってよい。
お値段は多少高めだが、作りはしっかりしているし、おそらく多少の雨でも平気。
今回、走りながらおにぎりが食べられたのは、このフレームバッグに依るところが大きい。
フレームバッグを付けるとロングボトルが取り出しにくくなるのだが、
その対策として横抜きボトルゲージ（TOPEAK デュアルサイドケージ）を取り付けた。

フレームバッグの中身：
　・食料（おにぎり、ウィダーインゼリー、朝食バー、ブラックサンダー）
　・おにぎり用ジップロック
　　　おにぎりはその場で“皮”をむいてジップロックに入れる。こうすると食べやすい。
　・レスキューシート（いざというときに役立つ）
　・予備チューブｘ２
　・財布（自販機用の小銭とコンビニ用Suica）
　・めがね（昼はサングラス、夜はめがねに切り替えている）
　・メットカバー

サドルバッグの中身：
　・携行ウィンドブレーカー
　・防寒用上着

ツールケース(シートチューブ・ボトルゲージ)の中身：

　・携帯ツールセット
　・予備チューブｘ１
　・Panaracer EASY Patch + ParkTool タイヤ応急パッチ
　・タイヤレバー
　・アーレンキー（よく使うサイズだけ特に）
　・小型プライヤー
　・マイナスドライバー（こじり用）
　・小型はさみ（100円ショップで購入）
　・ビニールテープ + ぼろ布
　・あと、ツールケースの横に小型フレームポンプを取り付けている。

携帯電話はランニング用のアームバンドポーチに入れ、エアロバーに取り付けている。
こうすると、走りながら携帯の地図が見れる。
ポーチの中には大きいお金（札）やカードも入れてある。

■ 事前準備
２週間前: 霞ヶ浦まで 150kmほどのライド。平均時速 25kmを体で覚える。
１週間前: 自転車は避け、足でロングジョギング 20kmほど。体長を整える。床屋で断髪式。

■ 経過
・朝 3:30に起床。朝食はしっかりと、おにぎり、やきそば、メロンパン、オレンジジュース。
　自宅から日本橋まではユルユルと自走。昨日の雨で道路はところどころ湿っている。
　4:30出発の予定だったが、多少遅れて 4:50に出発。

・都内は信号が多いので、焦らずじっくりと。
　甲州街道は昼間は混雑していて走りたくない道だが、早朝は空いている。
　調布から府中にかけては旧道を抜けた。早朝はほとんど車がおらず、本道より走りやすい。

・前回まで大垂水峠を避け、津久井湖を経由するルートを通っていたのだが、今回はまっすぐ峠に挑むことにした。
　津久井湖経由の方が 3km程度距離が長い。実際、ここで５分程度の時間短縮になった。

・大月、笹子トンネル、甲府をいい感じで通過。
　腹が減る前に早めの補給、おにぎり２個を走りつつ食べる。
　最初の休憩は釜無川河川緑地にて。
　毎回、このあたりでトイレに行きたくなるので立ち寄っている公園だ。
　今回もトイレ＋ボトルに水を補給。

・富士見峠への登り。
　過去、ここではメカトラ、パンク、あるいはペースダウンしていたものだが、
　今回はいたって順調。ノンストップで峠を越える。かつて無かった良いペース。
　そのためか今回は燃料消費が激しく、空腹がおそってきたので手持ちの食料を全て食べる。

・諏訪湖湖畔で自販機休憩。
　毎回悩まされていた強烈な向かい風が、今回は全く無い。
　塩尻峠９時間以内が最初の大きな目安のところ、余裕の８時間１５分で突破。
　成功への実感が湧く。

・いつもは塩尻峠を下ったあたりで疲れて休憩を入れていたのだが、今回はノンストップで通過できた。
　そのままの勢いで鳥居峠を越え、木曽福島の旧道へ。
　木曽福島は旧道の方がトンネルが無く、アップダウンも若干少ないようだ。
　ここで今回唯一のコンビニ補給。おにぎりとコーラで遅めの昼食を取る。

・木曽高速の豪快な下り。連休なのでトラックが少なめでよかった。
　後から記録を見ると、大桑〜坂下間は平均時速 36kmというスピードだった。
　実際、何kmで下ったかは推して知るべし！

・恵那市はバイパスを避け、旧道を通って市内を通過した。
　このあたりから名古屋に帰る車で渋滞が起こり始めた。
　恵那市の出口、まきがね公園前の自販機にて休憩（「いこい」というラーメン屋の脇）。
　この自販機も毎回休憩するポイントだ。

・断続的に生じる渋滞の脇をすり抜けるように通過。
　瑞浪、次いで土岐は、旧道を使って渋滞を回避する。

　国道19号に戻ってから、多治見を通過するまでが最も渋滞がひどかった。
　あせる気持ちを抑え、辛抱強く路肩ぎりぎりを走る。
　ただ、後から記録を見たところ、それほど大きなマイナスにはなっていなかった。

・内津峠を登り切れば、アップダウン区間も終わりだ。
　ここは通るたびにチャレンジ１回目の苦しかった思い出がよみがえるのだが、今回は軽めのギアで調子よく突破できた。
　いつもこの辺りから気温が下がってくるので上着を着用するところなのだが、今回は特に寒くならない。
　そのままの服装で先に進む。

・一宮市の公園でトイレ休憩、ボトルに給水。
　この前後は信号が多く、ややペースダウン。
　これまで平均時速 25km台だったサイコン表示が、ここで24km台まで下がった。

・過去に２回、関ヶ原で急に気温が１０℃以下まで下がってペースダウンすることがあったのだが、
　今回は気温１８℃と、全く問題無かった。このために用意しておいた上着は出番が無かった。

・関ヶ原を越え、米原でプラス１時間３０分の余裕があることを知り、ほぼ成功を確信した。
　ここから普段のペースで走りきれば２４時間以内は確実だ。
　ただ、眠気やパンク、思わぬトラブルが襲ってくるかもしれないので、まだ気は抜けない。

・彦根城の横をすり抜け、県道２号線を使って琵琶湖の東側を下る。
　こちらの方が国道８号より、俄然交通量が少ない。
　このあたりで眠気がピークに達したが、能登川付近の自販機で休憩を入れて気持ちを整えた。

・近江八幡付近で、こんな夜中にロードの一団と出会う。
　少しだけ同じ方向に走り、ほどなく分かれた。
　まあ、向こうもなんでこんな夜中に走っているのだろう、と思ったことだろう。

・近江大橋を渡り、膳所城跡公園にて最後のトイレ休憩。
　この公園も、いつも休憩するポイントとなった。
　公園から１号線へは、膳所本町駅の横をすり抜ける抜け道ルートを通る。
　（ただし、この抜け道は東京->大阪では意味があるが、逆の大阪->東京だと意味が無い。）

・逢坂の関、京都醍醐の回避ルートを抜け、京阪国道に入ればもうあとわずか。
　ここで最後の大福もちを補給、甘い物がやたらとおいしい。
　当初の計画では淀川サイクリングコースという案だったのだが、
　深夜に初めての道は危険であること、思ったより交通量が少なかったことから、
　王道の京阪国道を行くことにした。

・深夜 3:37、ついに梅田交差点に到着。
　長い、長い道程だった。

やれば、できるのだ。
当初、こんなことできるわけが無いと思っていた。
今回だって、２４時間以内に走りきれるとは思っていなかった。
それでも、やってみたら、できた。
大満足だ。
この喜びを、みんなに伝えたい。
本気でチャレンジするなら、キャノンボールは確かにやる価値がある。

■ 中仙道キャノボ・リンク
先人たちの記録。私も大いに参考としました。いくらでもすごい人はいるものだ。

* AZE: ミニベロでのキャノンボール挑戦，5度目にしてようやく達成！
https://blogs.yahoo.co.jp/aze84678/13236501.html

* ミニベロでキャノボ　中仙道 transamhide編
https://togetter.com/li/1026516

* 中山道キャノボ一旦のまとめ（軽井沢経由、フル中山道キャノンボール！）
https://togetter.com/li/1035059

* おあほさんといっしょ　（´∀｀）: 中山道キャノンボール（大阪→東京）準備編
http://asrafil.seesaa.net/article/443126193.html