なぜ分散は２乗の和なのか

Ｑ．なぜ分散は、単純な差（偏差の絶対値）ではなく、差の２乗を計算するのか？
Ａ．分散を最も小さくする点が平均値だから。（単純な差を最も小さくする点は中央値となる。）

“分散”というキーワードは統計学の基礎中の基礎であり、どんな教科書にも“平均”の次くらいに載っていることがらです。
しかしながら、いきなり登場する“分散”の意味が分からず、統計学の入り口で挫折する人は少なくありません。

偏差の２乗の平均、つまり、各値と平均との差の２乗の平均を分散といい、
分散の平方根の正の方を標準偏差という。
統計で、ちらばりを表すものとして、標準偏差や分散が多く用いられる。
　　　　　　-- 高校の教科書（啓林館）より.

教科書にはこのように書かれているのですが、これで分かった気になるでしょうか。
　・なぜ、差の２乗を計算するのか？
　・差そのものであってはいけないのか？
　・なぜ、分散と標準偏差の２種類があるのか？
最後の疑問については「分散が２乗した結果なので、元の単位に戻すために平方根をとる必要がある」のだと説明されます。
　　(標準偏差) ＝ √(分散)
だとすると、そもそも値を２種類作らなければならなかった理由は２乗を計算するからであって、
最初から差そのものを採用していれば１種類で済んだはずです。

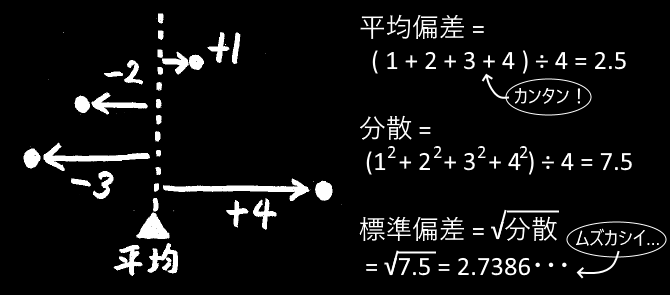
各データと平均値との差のことを「偏差」と言います。
分散とは、偏差を２乗した値の平均のことです。
一方、偏差の値そのもの（絶対値）の平均は「平均偏差」と呼ばれています。
分散（と標準偏差）に比べて、平均偏差はあまり有名ではありませんし、全ての教科書に載っているわけでもありません。

もし何の予備知識も無しに「ばらつきを数字で示せ」と言われたなら、
データの差そのものを持ってくる平均偏差の方がよほど自然に思えます。
なのになぜ、今日の統計では、ややこしい分散（と標準偏差）の方が主流なのでしょうか。
歴史を振り返ってみると、偏差の２乗が一般化する以前に、差そのものをばらつきの指標と捉えていた時期がありました。
例えばラプラスは、差そのものを誤差損失の指標として扱っていたという経緯があります。
はっきりと２乗を指標とするようになったのは、ガウスの登場以降のことなのです。

Laplaceはこのことを同じような方法で考察した。しかし彼は、つねに正として扱われる誤差自身を損失の量として選んだ。
　　　　-- ガウス誤差論より.

■ 最小２乗法のこころ

ではなぜ、ガウスは２乗を考えたのか。
その心を知るには、ガウスのお家芸である“最小２乗法”をひもとくのが早道です。
最小２乗法とは、誤差を含んだデータに対して、もっともよく当てはまる関係を見出す方法です。
例えば、とあるグループの身長と体重のデータが、こんな風だったとしましょう。

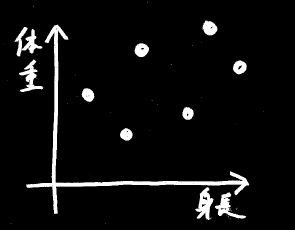
ここで「身長が高いほど体重が重い」という関係を１本の直線で示すには、どのように線を引くのがもっとも合理的でしょうか。
最小２乗法では、次のように考えます。

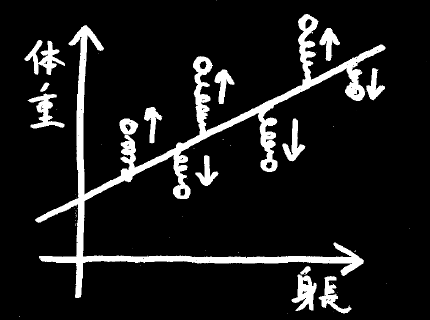
一本の棒と、それぞれのデータの間をバネで結んで引っ張ると、棒はほどよいところに落ち着きます。
この落ち着いた先の状態を「もっとも当てはまりが良い」と見なすのが、最小２乗法の考え方です。
なぜ２乗なのかというと、バネは引っ張れば引っ張るほど、長さに比例した力がかかるからです。
バネの長さを２倍に引き伸ばすには、
　・長さが２倍
　・力も２倍
合わせて２×２＝４倍のエネルギーが必要です。

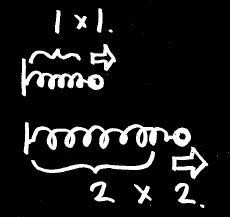
これが２乗の由来です。
最小２乗法とは、つまり「バネに溜まったエネルギーが最小となる位置を探す方法」のことだったのです。
* ∫ニョロっと伸びるはエネルギー、バネは答を知っている
>> http://miku.motion.ne.jp/multi/01_MinSquare.html

いま、２次元のグラフで見た方法を、さらに単純化して１次元としてみましょう。
複数個のデータと、自由に動かせる、とある１点をバネで結んだとしたら、とある１点はどこに落ち着くか。
落ち着く先は、ちょうどデータの平均値となります。

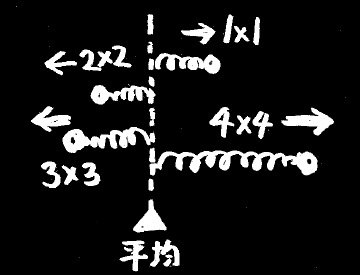
※ ２次元の場合、当てはめた直線（回帰直線）は必ず平均値を通ります。
平均値とは、「バネに溜まったエネルギーが最小となる点」のことだったのです。
そして「バネに溜まったエネルギー」とは、各データと平均との差の２乗、つまり分散に比例しています。
かくして手元のデータから、もっとも当てはまりの良い点を探そうと考えたとき、分散の最小化というアイデアに導かれるわけです。

■ 分散の加法性

ここで１つクイズ。
　『厚さが平均１cmの月刊誌を１年分積み上げたら、高さは平均で何cmになるか？』
答は当然、１２cm。
では次に、
　『その雑誌のばらつきは±１mmだった。１年分積み上げたとき、ばらつきは±何mmになるか？』
ここでの「ばらつきが±１mm」の意味ですが、話を単純化して、雑誌の厚さには 9mm と 11mm の２種類しか無くて、
その２種類が毎月ランダムに発行されるものとしましょう。

答の選択肢：１年分のばらつきは・・・
　(a) ±１２mm、　±１mm × 12ヶ月だから。
　(b) ±０mm、　　＋と－が打ち消し合って０になるので。
　(c) ±１２mm でも ±０mm でもない、中途半端な数。

　

　

　

　

　

　　　　・・・ちょっと考えてみよう・・・
　

　

　

　

　

正解は (c)。
試しに ±1 の乱数を１２個、何回も足し合わせた平均の絶対値をとると 2.7mm くらいの値となります。
（２項係数を用いて詳しく計算すると 2.70703125... といった値になります。）
つまり、ばらつきに関しては単純な足し算ができないということです。

何とか上手い具合に“ばらつきの足し算”ができないものだろうか・・・
そこで編み出されたのが「２乗すれば足し算できる」というアイデアです。
±１mm の乱数が１２個あったとして、それぞれをただ足し合わせるのではなく、２乗して足し合わせてみましょう。
　　(±1)^2 + (±1)^2 + (±1)^2 + ･･･ ±1)^2 = 12
これなら個々のばらつきがプラスであってもマイナスであっても、合計は確実に+12となるでしょう。
このように、２乗した値によってばらつきを数えたのが、分散という指標だったのです。
　・雑誌１冊あたりの分散 　　＝ 　１
　・12冊積み重ねた全体の分散 ＝ １２
　　　※12冊のサンプルがたくさんあったときの分散。つまり毎年の雑誌の山をたくさん並べたときのばらつき。

分散は足し算することができる。
この性質を分散の加法性と言うことがあります。
むしろ、足し算ができるような指標を探したところ、うまくいったのが分散であった、というのが実情でしょう。

では、雑誌１年分の分散が12だったとして、実際に雑誌の山の高さは±何mm程度なのでしょうか。
そこで分散の平方根をとって、元の次元に戻したのが標準偏差です。
今の場合、
　　(標準偏差) = √12 = 3.46mm
といった値となります。
※ 標準偏差 3.46mm は、少し上に書いた平均偏差 2.71mm とは異なります。
※ 標準偏差は偏差２乗和の平均、平均偏差は偏差絶対値の平均です ← しつこいようですが、ここんとこよく間違うので。

■ 分散のエネルギー解釈

　・分散とは「バネに溜まったエネルギー」のこと。
　・分散とは「足し算できるように」編み出されたばらつきの指標。

この２つが「なぜ分散が２乗なのか」についての主な答になると思います。
さらに穿った見方をするならば、この２つは別々の事柄ではなく、共通の内容を含んでいると解釈することもできるでしょう。

そもそもエネルギーとは何だったかといえば、
　「物理的に、時間変化に対して不変な保存量」
のことでした。
何らかのデータ操作について、例えば上に述べた“バネと棒”のような物理的なモデルを考えたなら、
そのモデル上で足し算できる保存量は、自ずとエネルギーに対応付けられるはずです。
こと分散については、「変位の２乗で溜まるエネルギーのような保存量」というイメージで把握できると思います。
この線で標準偏差に解釈を加えるなら、
　「各データにエネルギーを等しく分配したとき、１個あたりのデータが変位する大きさ」
ということになります。

■ 最小絶対値法ではダメなのか

以上、分散（と標準偏差）が、いかにばらつきの指標として合理的であるかを見てきました。
ならば、ばらつきの指標は分散だけが唯一無二であり、それ以外にはあり得ないのでしょうか。
実はそうでも無いのです。
分散は、一般的には最も優れた指標なのですが、場合によっては分散以外の指標が有用なこともあります。
先に、分散 ～ 最小２乗法に基づいてデータの当てはまりを考えたのですが、
次に、偏差の値そのもの ～ “最小絶対値法”に基づくデータの当てはまりを考えてみましょう。

１次元の場合、もしデータが２つだけだったなら、
もっとも当てはまりの良い点は、２つのデータの間のどこでも良いことになります。

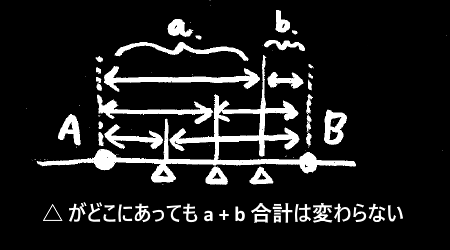
このように最小絶対値法には、結果が１点に落ち着かないといった不定性があります。
これが最小絶対値法 ～ 平均偏差が流行らない１つの理由です。
データの数をもう少し増やしてみましょう。
もしデータが５つだったなら、最小絶対値法によるもっとも当てはまりの良い点は、中央の３番目の点になります。

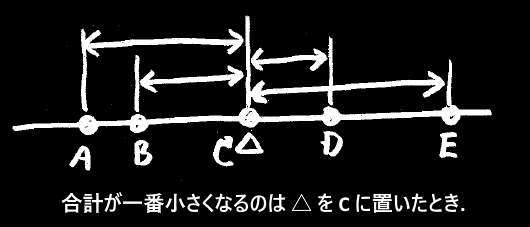
平均偏差を基準に考えたなら、
　・データが奇数個の場合、順位が中央の点となる。
　・データが偶数個の場合、順位が中央に最も近い２点の間のどこでもよい。
つまりこれは「中央値」ということです。
※ 中央値の定義としては、データが偶数個の場合、中央に最も近い２点のちょうど中間（平均）となります。

・分散　　　：偏差の２乗の平均値　　：　最小２乗法　　：　最小となる点は平均値
・平均偏差　：偏差の絶対値の平均値　：　最小絶対値法　：　最小となる点は中央値

このように対比させてみれば、決して“分散が優れていて、平均偏差が劣っている”わけでは無いのだと分かるでしょう。

さらに興味深いのは、２次元の場合です。
一般によく用いられている最小２乗法ではなく、最小絶対値法による直線の当てはめも、それはそれでアリなのです。

* 最小絶対値法による回帰分析
>> http://www.orsj.or.jp/~archive/pdf/e_mag/Vol.40_02_261.pdf
* 最小二乗と最小絶対値：ロバスト回帰で外れ値分析
>>https://biolab.sakura.ne.jp/robust-regression.html
* Excelで操る！誤差の絶対値和を最小にする
>> http://godfoot.world.coocan.jp/Abs_Min.htm

最初のリンク先に、ラプラスの考えた最小絶対値に基づく方法が載っていました。

この回帰分析規準（1）を最良のものと考え，そのアルゴリズムを最初に提案したのはLaplace［PiereSimmonMarquisdeLaplace，1749－1827］である。

リンク先の説明を参考に、ラプラスの考えた直線当てはめの方法を試してみました。

・原点を通る直線を考える。
・各データを傾きの順番に並べる　Y1/X1 >= Y2/X2 >= Y3/X3 ･･･ Yn/Xn
・X1 + X2 + X3 ･･･ + Xr-1 < Xr + Xr+1 + Xr+2 ･･･ + Xn　かつ
　X1 + X2 + X3 ･･･ + Xr > Xr+1 + Xr+2 ･･･ + Xn　となる r を探す。
　つまり、傾きの大きい方から X を合計していって、合計値が残りの合計をちょうど越える番号 r を探す。
・最も当てはまりのよい傾きとして、Yr/Xr を採用する。

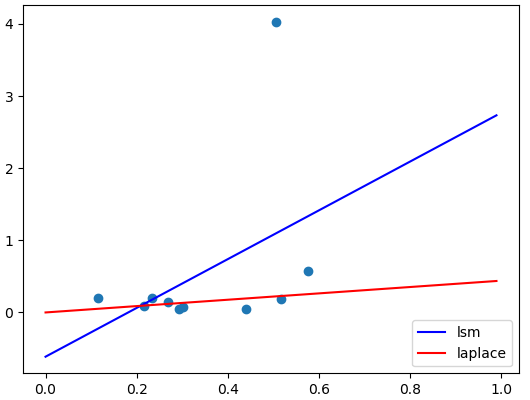
これは当てはめ結果の１例です。
青線が最小２乗法、赤線がラプラスの考えた最小絶対値法です。
この例のように極端な外れ値が混じっていた場合、最小２乗法は外れ値に引っ張られるため当てはまりが悪くなります。
中央値が平均値に比べて外れ値に強いように、最小絶対値法には外れ値に対して頑健な性質があります。

回帰分析のあてあまり評価の指標として、RMSE, または MAE という値がよく用いられます。
これらは何なのかというと、分散と平均偏差、あるいは平均値と中央値、という並びに位置づけられるものです。

* 平均平方二乗誤差 = RMSE（Root Mean Square Error）
・RMSE の最小化 = 二乗誤差の最小化 = 誤差に正規分布を仮定した場合の最尤推定
* 平均絶対誤差 = MAE（Mean Absolute Error）
・MAE の最小化 = 絶対誤差の最小化 = 誤差にラプラス分布を仮定した場合の最尤推定
　-- 精度評価指標と回帰モデルの評価
　>> https://funatsu-lab.github.io/open-course-ware/basic-theory/accuracy-index/

あるいは最近流行りの機械学習に登場する L1正則化(Lasso), L2正則化(Ridge) といったキーワードも、やはりこれらの概念の延長上に位置づけられます。

■ ガウス誤差論より

なぜ２乗なのか、その源流を遡ると、ガウスの誤差論にたどり着きます。

確かに２乗は優れた概念なのだが、ならば２乗を支える根拠・原理は何なのか。２乗以外の概念はあり得ないのか。
私は長らくこの疑問を抱いてきたのですが、元祖ガウスの言葉にようやく答を見たように思います。
今さらですが、（推測）統計学とはデータから帰納的に導かれるものであり、
他の数学のように原理原則から演繹的に導かれるものではありません。
その意味で、２乗が唯一絶対の方法では無かったのです。
ただ、いったん２乗を離れて他のあらゆる方法と比べてみると、改めて２乗こそが最も単純で適していると認めざるを得ません。
これが分散を２乗で数える理由であり、今日に至るまで統計学の根底に流れ続ける基盤だったのです。

誤差論

■ Python による Laplaceの絶対値回帰

# -*- coding: utf-8 -*-
#
# Laplaceの絶対値回帰

import numpy as np
import matplotlib.pyplot as plt

# 直線回帰を行う
def fit_line(x, y):
    mx = np.mean(x)
    my = np.mean(y)
    myx = np.mean(y * x)
    mxx = np.mean(x * x)
    w0 = (myx - my * mx ) / (mxx - mx ** 2)
    w1 = my - w0 * mx
    return ( w0, w1 )

# 適当な直線＋乱数データを用意
N_SAMPLE = 10
ALPHA = 0.0  # 切片は０に限定する
BETA = 0.3
EPS = 0.1

X = np.random.rand(N_SAMPLE)
# Y = ALPHA + BETA * X + np.random.normal(0, EPS, N_SAMPLE)     # 正規乱数
# Y = ALPHA + BETA * X + EPS * (np.random.rand(N_SAMPLE) - 0.5)   # 一様乱数
Y = ALPHA + BETA * X + EPS * np.random.standard_cauchy(size=N_SAMPLE) # コーシー分布
    # この場合、Laplace回帰はけっこういい感じだ
# Y = ALPHA + BETA * X + np.random.laplace(loc=0.0, scale=EPS, size=N_SAMPLE) # ラプラス分布
    # Laplace回帰が最尤値になるという。

####
# まずは普通の線形回帰をやってみよう
lin, seg = fit_line( X, Y )
print( "線形回帰の傾き,切片 = {:.4f}, {:04f}".format( lin, seg ) )

####
# 以下、Laplaceの考えた方法で回帰をやってみる
YperX =Y / X   # 個々の点の傾きリスト

Slp_index = {}  # index->傾きリストを作る
for idx in range(N_SAMPLE):
    Slp_index[idx] = YperX[idx]

# 傾きの値で降順にソートする
x_list = []
idx_list = []
for key, val in sorted(Slp_index.items(), key=lambda x: -x[1]):
    # print( "{{ {} : {} }}, X={}".format( key, val, X[key] ) )
    idx_list.append(key)
    x_list.append( X[key] )

# Xの前半の合計値が後半の合計値を越える境界を探す
r_index = 0
for r in range( N_SAMPLE+1 ):
    pre  = x_list[ 0 : r ]              # 前半
    post = x_list[ r : len(x_list)+1 ]  # 後半
    if sum(pre) >= sum(post):
        # print( "Pre:", pre, "len=", len(pre) )
        # print( "Post:", post, "len=", len(post) )
        r_index = r -1  # インデックスなので１引く。
        break

x_esti = idx_list[ r_index ]
# print( "x_ans={}, X={}, YperX={}".format( x_ans, X[x_esti], YperX[x_esti] ) )

lap = YperX[x_esti]
print( "Laplace回帰の傾き = {:.4f}".format( lap ) )

# グラフ出力
xlist = np.arange(0, 1, 0.01) # 0.01単位で細かくプロットし、線として出力させる
ylist_lsq = [ (lin * x + seg) for x in xlist ] # 線形回帰
ylist_lap = [ (lap * x) for x in xlist ] # Laplaceによる回帰

plt.plot(X, Y, 'o') # 元データ
plt.plot(xlist, ylist_lsq, color="blue", label="lsm")       # 線形回帰
plt.plot(xlist, ylist_lap, color="red", label="laplace")    # Laplaceによる回帰

plt.legend(loc='lower right')

plt.show()