シュレーディンガー方程式を行列風に描く
シュレーディンガー方程式とは、量子力学の基礎となる方程式、つまりあらゆる物質の振る舞いを記述する方程式です。
このシュレーディンガー方程式、確かに難解な代物には違いないのですが、
それでも幾つかのコツを掴みさえすれば、かなり身近に引き寄せることが可能です。
以下に書くのは、そうしたコツの中の1つ、「線形性」という性質についてです。
シュレーディンガー方程式には、線形性、固有値、固有関数といった、行列(線形代数)に関わるキーワードが付いて回ります。
それでは一体、この方程式のどこがどう行列になっているのでしょうか?
一見すると、シュレーディンガー方程式は単なる一行の数式であって、
数字記号を縦横に並べた行列とは何の関係も無いように思えるのですが・・・
しかし、たとえ縦横に並べて書いてなくても、この方程式は実質的に行列の計算と同じことを行っているのです。
【1】.波動関数とは、ベクトルの次元を無限に細かく刻んだ極限の姿である.
【2】.演算子とは、行列を無限に細かく刻んだ極限の姿である.
【3】.シュレーディンガー方程式とは、行列xベクトルを無限に細かく刻んだ極限の姿である.
【1】.シュレーディンガー方程式の正体を探るため、まず「波動関数を状態ベクトルに戻して」みましょう。
量子力学では、あらゆる粒子(電子とか、光子とかいったもの)は波動関数で表されます。
ここで詳しい解釈は行いませんが、とにかく物体の存在は「点」ではなくて、
関数で表されるような「広がりを持ったもの」であるとしましょう。
関数というものは一般には連続的に、滑らかに変化するものなのですが、
ここでは一旦、波動関数をデジタル化して、細かい階段の集まりだと見なします。
一昔前の画素の荒いパソコンに入れて、カクカクにしたのだと思ってください。
このカクカクした関数の階段の高さを、先頭から順番に記録します。
記録した数字を一列に並べたものが「状態ベクトル」です。
つまり、関数というものは、デジタル化すれば一列の数字の並びに置き換えられるのです。
量子力学の場合、この数字は複素数の並びとなります。
階段をうんと細かくすれば、数字の並びは無限に長くなるでしょう。
それをカッコよく言えば「複素無限次元状態ベクトル」てなことになるわけです。
【2】.シュレーディンガー方程式に登場する主だたる記号は「演算子」です。
演算子とは、関数に作用して、新たな別の関数を作り出すモノのことです。
量子力学では、波動関数に作用して、位置や運動量といった物理量を作り出すモノとして用いられています。
ここで、波動関数を状態ベクトル=数字の列に戻したことをイメージしてみてください。
すると、演算子というものは、数字の列(ベクトル)に作用して、別の数字の列を作り出すもの・・・
つまり演算子とはベクトルを変換する行列であることに気付くでしょう。
具体的に、粒子の位置を表す、位置演算子の行列を考えてみましょう。
量子力学では、波動関数に位置の演算子xを掛けたものが、粒子の位置(の期待値)を表すのだとされています。
このことを行列っぽく書くと、どうなるか。
まず波動関数を、上の「状態ベクトル」の考え方に従って、数字の並びにします。
この数字の並びに「xを掛ける」とは、
・距離0の位置にある数字には0を掛ける.
・距離1の位置にある数字には1を掛ける.
・距離2の位置にある数字には2を掛ける.
・・・
つまり位置の演算子を行列にすると
こんな感じになるわけです。
# ここでおやっ?!と感じるのは、波動関数=位置ではない、ということでしょうか。
# 粒子の位置は、波動関数に上記のような操作を施して初めて出てくるものなのです。
# それでは、波動関数っていったい何?と聞かれると、
# 位置や運動量の元になる情報を含んだモヤモヤした何か、としか言いようがありません。。。
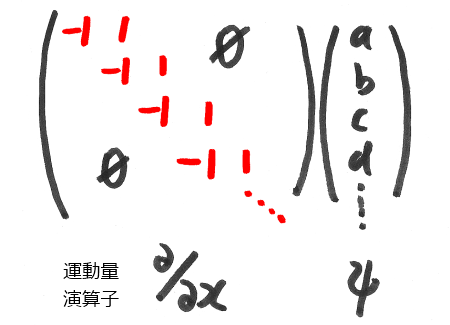
次に、運動量の演算子を行列っぽく書いてみましょう。
運動量の演算子とは、-ih~(∂/∂x) 、つまり波動関数の微分に虚数iと定数(プランク定数/2π)を掛けたものです。
とりあえず定数部分は後回しにして、微分のところを行列にすることを考えます。
そもそも微分とは何だったかと言えば、「すぐ隣との差分」を表すものでした。
「すぐ隣との差分」を状態ベクトルの数字の並びにあてはめれば、
・1番目=すぐ隣の2番目から1番目自身の値を引く.
・2番目=すぐ隣の3番目から2番目自身の値を引く.
・3番目=すぐ隣の4番目から3番目自身の値を引く.
・・・
ということになります。
これを行列にすると、こんな感じです。
# 運動とは、隣と差のある部分に、高いところから低いところに流れるようにして生じる。
# そのように私は理解しています。
さらに、エネルギーの演算子(ハミルトニアン)を行列っぽくすると、どうなるか。
(ポテンシャル=0の)エネルギー演算子は、-(ih~ ^2 / 2m)(∂^2/∂x^2)、
定数の部分を省けば、要は波動関数の2階微分ということです。
2階微分とは、微分の微分、つまり「前後に渡る変化」を表したものです。
「前後に渡る変化」を状態ベクトルの数字の並びにあてはめれば、
・2番目=右隣の3番目+左隣の1番目から2番目自身の値x2を引く.
・3番目=右隣の4番目+左隣の2番目から2番目自身の値x2を引く.
・4番目=右隣の5番目+左隣の3番目から2番目自身の値x2を引く.
・・・
行列にすると、こんな感じ。
ここでちょっと、後回しにしていたプランク定数h と、虚数i の意味を考えてみましょう。
まずはプランク定数について。
上では何も考えず、行列の幅(1区画)を適当に1,2,3・・・と数えていました。
運動量の行列を例にとると、上のように、全ての非ゼロの要素を「1」だとするのが最も自然ですが、
別にこれが「2」であっても、「0.35」であっても、働きとしては同じでしょう。
では、この行列要素の数字は幾つにするのが妥当なのか。
その答は、この行列を極限まで細かくしていったとき、値がどこに収束するかによって決まるはずです。
そこで、行列の極限をとった値と、実際の物理的な観測結果を比較して、出てきた値がプランク定数だったのです。
つまりプランク定数とは、行列を極限まで細かくしていったときの収束先なのです。
次に、虚数i の意味についてですが・・・ぶっちゃけて言えば、
「位置と運動量という2つの値を同時に保持できるのが複素数であった」のだと、私は思っています。
物体の運動は、本質的に位置と運動量という、2つの値で記述することができます。
この2つの値は「運動量を微分すると位置になる」という関係で結ばれています。
古典力学の場合には、位置も運動量もそれぞれただ1つの数字で表すことができたので、
素直に2つの実数を用意すれば事足りていました。
ところが量子力学では、位置も運動量も「広がりを持って」おり、ただ1つの数字で表すことができません。
望まれるのは「2つの値を併せ持つ、広がりを持った関数」です。
そんな容れ物を数学の中から探してみたところ、「複素数の関数」がちょうどぴったりあてはまった、というわけです。
複素数は、実数と虚数、2つの値を保持しています。
そこで、一方の実数を位置に、もう一方の虚数を運動量にあてはめたところ、何とも上手い具合に納まった。
それが波動関数の正体であり、運動量に虚数i を掛ける理由です。
【3】.波動関数 -> 状態ベクトルと、演算子 -> 行列の意味がわかれば、
シュレーディンガー方程式全体の意味が見えてきます。
まず、波動関数が定常的で動かない場合、時間に依存しないシュレーディンガー方程式を取り上げます。
この時間に依存しない方程式は「固有方程式」の一種であり、式に登場するエネルギーEは「固有値」に対応付けられる。
・・・そのように、多くの教科書に書かれているのですが、この「固有方程式」とは一体何なのか。
その意味は、行列っぽく書いてみるとはっきりします。
行列によって変換したベクトルが、もとのベクトルに重なるとき、そのベクトルのことを「固有ベクトル」と呼んでいます。
変換の前後で、固有ベクトルの大きさが何倍に拡大(縮小)したのか、その値のことを「固有値」と言います。
変換行列が与えられたとき、その行列に対する「固有ベクトル」と「固有値」を求める方程式が「固有方程式」です。
* 固有ベクトルが直交するのは >> [id:rikunora:20090307]、その2 >> [id:rikunora:20110203]
以上は線形代数の予備知識。
で、時間に依存しないシュレーディンガー方程式は、その固有方程式と全く同じ構造を持っているのです。
ベクトルに相当するものは、波動関数=状態ベクトル=複素数を一列に並べたもの。
変換行列に相当するものは、エネルギー演算子、つまり「ベクトルを2階微分せよ」という変換。
固有値に相当するのがエネルギー、つまりベクトルの定数倍。
以上をあてはめると、時間に依存しないシュレーディンガー方程式とは、
要するに「2階微分しても形が変わらないものを探せ」と言っているわけです。
「2階微分しても形が変わらないもの」とは、具体的にどんな形をしているのでしょうか。
まず、指数関数が答の候補に挙がります。
指数関数は、何回微分しても形が変わりません。
なので「2階微分しても形が変わらないもの」になっています。
しかし、指数関数は遠くにいくほど無限に大きくなります。
無限に大きくなるものが、物理的に1個の電子や光子のような粒子であるとは考えにくい。
なので、残念ながら指数関数は物理的な答には成り得ません。
それでは、指数関数を複素数にしたら、どうでしょうか。
実は、この複素数の指数関数、Exp(ix) といった形の関数が、基本かつ重要な答の1つなのです。
全く制限の無い、自由な空間に置かれた粒子の運動は、複素数の指数関数といった形であると考えられます。
* 複素数の指数関数 >> [id:rikunora:20090607]
* 電子のカタチ >> [id:rikunora:20101226]
複素数の指数関数の実数部分は、三角関数となっています。
(あるいは複素数の指数関数を組み合わせることで、三角関数を作ることができます)
ということは、Sin とか Cos といった三角関数も、答になっているのではないか。
実際、Sin を2階微分すると、(符号は反対になるけれど)また Sin に戻ってくるので、
三角関数もまた方程式の解と成り得ることがわかります。
つまりこれが「波動」の言われだったのですね。
時間に依存しないシュレーディンガー方程式の仕組みが分かれば、
より一般的な、時間変化のあるシュレーディンガー方程式についても想像が及ぶでしょう。
時間変化のあるシュレーディンガー方程式とは、時間に依存しない場合の固有値E(エネルギー)を、
ih~(∂/∂t) に置き換えたものです。
この ih~(∂/∂t) の部分は、先に挙げた運動量の演算子 -ih~(∂/∂x) にそっくりです。
ただ、時間tと位置xが異なっているだけ。
波動関数が「動いている」場合、空間xに対する運動と似たようなものを、時間tについて行えば良い。
つまり、波動関数は「時間方向に動いている」のだと解釈できるでしょう。
・・・これが私流の時間変化の覚え方です。
以上、シュレーディンガー方程式を理解するコツをまとめると、
【1】.波動関数を、数字の並び=状態ベクトルと見なす.
【2】.演算子を、ベクトルを変換するもの=行列と見なす.
【3】.定常的なシュレーディンガー方程式を、固有方程式と見なす.
という3点になります。
# そんなの常識なのかな?!
# すごくセンスのある人なら「線形性」というキーワードを聞いただけで、
# 行列メカニズムが一気に理解できるのかもしれません。
# しかし、私自身はそうではなくて、
# 「シュレーディンガー方程式の、どこをどういじれば行列になるのだろう?」
# という疑問をずっと抱いていました。
# なお、ここに書いた「行列っぽいもの」は、「ハイゼンベルグの行列力学」とは別ものなので、混同しないように。