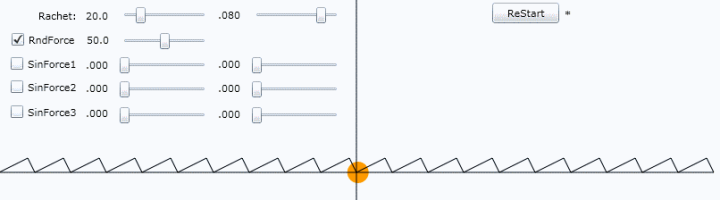
ラチェットとゆらぎ
のこぎりの歯のように、非対称でギザギザな地形の上に、小さなボールを置いたとします。
この地形全体をユサユサ揺さぶったら、ボールはどちら側に動くでしょうか?
直観的には、ボールはのこぎりの歯に引っかかるので、左側に動くような気がするのですが・・・
そこで、ボールの動きをシミュレーションによって確かめてみました。
* 確率的ラチェット(要:Silverlight 4)
>> http://brownian.motion.ne.jp/memo/Ratchet01/
シミュレーション画面の、一番上にある2つのスライドバーによって、ラチェットの高さと傾きを調整します。
左上の RndForce にチェックを入れると、ランダムな揺さぶる力が加わります。
(RndForce の右隣のスライドバーは、ランダムな力の大きさ調整)
【1】まず、ラチェットの形を左右対称にしたまま(スライドバー=.050)揺さぶってみます。
100回の試行のうち、左にはみ出した回数51回、右にはみ出した回数49回。
当然ながら、左右で5分5分に分かれました。
【2】次に、ラチェットの形を右側に寄せて(スライドバー=.080)揺さぶってみると、
100回の試行のうち、左が回数52回、右が回数48回。
ラチェットの形を変えても、結果は5分5分のままのようです。
【3】ラチェットの形を左側に寄せて(スライドバー=.020)揺さぶってみると、
100回の試行のうち、左が回数54回、右が回数46回。
やっぱり5分5分でした。。。
ランダムに揺さぶった場合、直観に反して、ラチェットの形をどのように変えてもボールは左右5分5分に動くようです。
なぜ、ボールは一方向に動かないのでしょうか。
この図は、有名な永久機関の一例です。
非対称な三角形の周囲に鎖を掛けたなら、左側の鎖の方が長くて重くなるので、鎖の全体は左向きに回るのでしょうか?
やってみればすぐ分かることですが、どんな形状に鎖をかけても、決して一方向に回ることはありません。
ラチェットとボールも、この鎖の例と同じことなのです。
現実にラチェットのような機構が一方向に機能しているのには、実は摩擦が重要な役割を果たしています。
もし摩擦が無かったなら、ここでのシミュレーションのように、ラチェットが一方向に機能することは無いでしょう。
何とかしてボールを一方向に動かすことはできないものでしょうか。
ランダムな力ではなくて、周期的に、上手いタイミングで力を加えてみたらどうなるか。
次に、ボールを一定の周期で揺さぶってみました。
【4】ラチェットの高さを(スライドバー=32.0)、形を右側に寄せて(スライドバー=.080)、Sin波に従った一定周期の力を加えてみる。
上から2番目のSinForce1にチェックを入れ、その右横にあるスライドバーを、それぞれ(強度=10.000)、(周波数=.725)とする。
ここで加えるSin波は、初期位相をランダムに変えています。(そうしないと、毎回全く同じ結果が出るので)
結果、100回の試行のうち、左が回数64回、右が回数36回。
明らかに左が多くなりました。(もし左右が同じだとすると、ここまで偏る確率は0.3%程度)
【5】ラチェットの向きを左右反対にして(スライドバー=.020)、上の【4】と同じことをやってみた。
結果、100回の試行のうち、左が回数44回、右が回数56回。(偏る確率13.6%)
150回の試行のうち、左が回数68回、右が回数82回。
上の【4】ほどはっきりしなかったので、少し多めに繰り返してみました。
今度は【4】とは逆に、右側が多くなっています。
Sin波のようにボールを一定の周期で揺さぶった場合、ランダムな場合と違って、一方向への偏りが見られます。
ただ、Sin波であれば必ず偏りがあるのかというと、そう言うわけでもありません。
実は上の【4】【5】は、スライドバーの値を試行錯誤で2〜3回変えてみて、偏りそうなところを探し当てた結果なのです。
まず、Sin波の大きさ(強度のスライドバーの値)が小さすぎると、偏りが生じないようです。
強度をある程度以上大きくして、周波数を調整すると、ボールがタイミングよくサーフィンのように走り出すポイントがあります。
Sin波でのボールの動きは、ランダムな力と比べると明らに違っています。
ランダムな場合、ボールは単純に行ったり来たりを繰り返すのですが、
Sin波の場合、ボールが一度走り出すと、勢いが付いて一気に幾つかの山をツツーッと通過する様子が見られます。
この、ツツーッの長さがうんと長くなると、【4】【5】のような偏りが見られるようになります。
ランダムな力と、一定周期のSin波の力とでは、何か本質的な違いがあるようです。
それでは、Sin波の周期を乱したら、ボールの動きはランダムに近づいてくるのでしょうか。
そこで、Sin波をグチャグチャに混ぜた状態、周期の異なる複数のSin波を重ねて揺さぶることを考えます。
Sin波を重ねる、とは、こんなイメージです。
このグラフは、大きさと周期の異なる3つのSin波です。
このうちの2個のSin波を足し合わせると、こんな感じに「うなり」の状態になります。
さらに、3つとも足し合わせてみると、より波形が崩れた感じになります。
こんな感じに、4つ、5つと、たくさんの波を重ね合わせれば、
最後にはグチャグチャになって、ランダムと同じ状態になるのではないでしょうか。
以上のアイデアに基づいて、まずSin波を2つ重ね合わせた力でボールを揺さぶってみました。
【6】Sin波2個の重ね合わせ、ラチェットの形は右寄り(スライドバー=.080)。
(1回目)100回の試行のうち、左が回数62回、右が回数38回。(偏る確率 1.0%)
(2回目)100回の試行のうち、左が回数59回、右が回数41回。(偏る確率 4.4%)
かなり偏っています。
【7】Sin波2個の重ね合わせ、ラチェットの形は左寄り(スライドバー=.020)。
(1回目)100回の試行のうち、左が回数48回、右が回数52回。(偏る確率38.2%)
(2回目)100回の試行のうち、左が回数41回、右が回数59回。(偏る確率 4.4%)
それなりに偏っているかな。
次いで、Sin波を3つ重ね合わせた力でボールを揺さぶってみました。
【8】Sin波3個の重ね合わせ、ラチェットの形は右寄り(スライドバー=.080)。
100回の試行のうち、左が回数56回、右が回数44回。(偏る確率13.6%)
わずかに偏っているかな。
【9】Sin波3個の重ね合わせ、ラチェットの形は左寄り(スライドバー=.020)。
100回の試行のうち、左が回数45回、右が回数55回。(偏る確率18.4%)
偏っているかどうか、はっきりしない。
これだけの結果では、あまりはっきりしたことは言えないのですが、どうやら
・たくさん重ね合わせた方がランダムに近づいている。
・3つ重ねた程度では、Sin波のクセを完全に消し去ることは難しい。
といった傾向があるようです。
たくさんのSin波を重ね合わせて、ランダムな力を再現することはできるのでしょうか。
その答は、フーリエ変換という数学的な手法によって確かめられています。
まず、ランダムな力についてですが、このシミュレーションでは左右に50%,50%の確率で、小さな一定の力を加えています。
こうした50%,50%の力を何度も加え続けると、力の積算結果は正規分布(ガウス分布)に近づきます。
この正規分布をフーリエ変換すると、Sin波の重ね合せに分解することができます。(連続、非連続の違いには目をつぶって)
分解した結果によると、Sin波をExp(1/周波数の2乗)の強度で重ね合わせれば、正規分布に近づく、ということが分かっています。
(正規分布のフーリエ変換は、実はまた正規分布となるのです。)
このシミュレーションで言えば、(強度) = Exp(1/(周波数)^2) という関係に従ってスライドバーを調整すれば、最もランダムに近いということになるでしょう。
ところで、波の持つエネルギーは、ちょうど周波数の2乗に比例します。
そのことからすると、重ね合わせる個々のSin波の持つエネルギーが、指数的に減衰している全て等しいときが、最もランダムな状態であると言えます。
逆に言えば、どれか1個のSin波が突出していたり、欠けていたりすれば、それだけランダムな状態からは離れている
〜 何らかの規則性を有しているのだと言えそうです。
ラチェットとボールにはおもしろい性質があって、
・全くのランダムだと、左右5分5分になる。
・ランダムな状態から外れるに従って、どちらか一方への偏りが強くなる。
つまりこのラチェットとボールは、「ランダム-規則性判定機」の役割を果たしているわけです。
今回のシミュレーションは、以前に紹介した以下の記事について掘り下げたものです。
* 奇跡も、魔法も、あるんだよ >> d:id:rikunora:20120619
こんな簡単なシミュレーションでも、イメージを掴むにはかなり役立ちます。
ただ、これで何か目新しいことがわかったかというと、依然、謎は謎のままですなー。