公平な不平等、不公平な平等
長さ1000cmの棒を一様乱数で1000個に切り分けたら、どんな長さの破片ができるか?
1cmの破片が1000個できるのかな、と想像しがちなところですが、実際にはこうなります。
これはパソコンでシミュレーションした結果のヒストグラムです。
確かに破片1個の“平均”は1cmなのですが、数で言えば平均以下の小さい破片の方がずっと多く、
その一方で、ごく小数の極端に長い破片があります。
最も数が多いのは、最も短い0.0〜0.18cmで、ここに160個以上の破片が含まれています。
反対に、最も長いものは 8cm以上、次いで7cm台、6cm台にも、ごく少数の破片があります。
以上は、ほんの数行のPythonスクリプトで確かめることができます。
# 長い棒を一様乱数で切ったら、破片の分布はどうなる? import numpy as np import matplotlib.pyplot as plt rds = np.sort(np.random.rand(1000) * 1000) # 1000個の乱数をソート sample = [ rds[i+1] - rds[i] for i in range(rds.size-1) ] # 乱数の間隔を取得する sample[-1] = rds[0] + (1000 - rds[-1]) # 最後は末尾と先頭をつなげる plt.hist( sample, bins=50 ) plt.show()
たとえPytonを知らなくても、エクセルで1000個の乱数を作って試すこともできます。
手間を厭わなければ、実験して確かめることもできます。 >> [id:rikunora:20091213]
これがタイトルに掲げた「公平な不平等」です。
乱数は公平です。しかし、公平な乱数で分配した結果は、不平等なのです。
“公平=平等”という思い込みは、必ずしも正しくありません。
似たようなことを、交換によって確かめてみましょう。
・1000人が当初1.0ずつの財産を持ち、お互いにランダムに財産を交換する。
・交換は、ランダムに選んだ2人がお互いの財産を出し合い、それを一様乱数によって振り分ける。
・交換を10万回繰り返す。
結果はこうなりました。
赤い線は「指数分布」と呼ばれている曲線で、理論上はこうなる、という形です。
さらに、交換のルールを少し変えてみましょう。
・1000人が当初1.0ずつの財産を持ち、お互いにランダムに財産を交換する。
・交換は、ランダムに選んだ2人が少ない方を越えない財産を出し合い、それを一様乱数によって振り分ける。
・交換を10万回繰り返す。
先ほどとの違いは「少ない方を越えない」という点で、たとえ少ない方が負けても全財産を失わないようにとの配慮からです。
結果は極端で、ごく一握りの勝ち組以外、大半はほとんど0になります。
なぜこうなるかと言うと、いったん財産が0近くになると、そこから抜け出すのが極めて困難だからです。
これでは余りにも勝ち負けがはっきりしているので、ハンディを付けましょう。
・交換は、ランダムに選んだ2人の財産の2乗の和が一定になるように乱数で振り分ける。
どういうことかと言うと、金持ちは持てる財産の大きさに比例してハンディを負え、というルールです。
先ほどより、だいぶ平等に近づきました。
※ 赤い線は「ガンマ分布」と呼ばれている曲線です。
※ なんとなく当てはまりそうですが、理論的にこれが正解なのかどうか、私にはよく分かりません。
もっともっとハンディを付けたら、どうなるか。
・交換は、ランダムに選んだ2人の財産の3乗の和が一定になるように乱数で振り分ける。
金持ちは持てる財産の2乗に比例してハンディを負えという、かなり金持ちに厳しいルールです。
さらに平等に近づいてきました。
反対に、金持ちが有利になるようなハンディを付けてみたら、どうなるか。
・交換は、ランダムに選んだ2人の財産の平方根の和が一定になるように乱数で振り分ける。
予想通り、かなり不平等な結果となりました。
以上の結果をまとめて描くと、こうなります。
このグラフは、分配ルールのハンディ乗数を0.5(平方根)〜4.0まで、0.5刻みに変えた結果を重ねて描いたものです。
(人数は8000人に増やしています。)
ハンディの大きさに応じて、結果が格差から平等に変わる様子が見て取れることと思います。
昔から言い古されてきたことなのですが、自由とは格差社会であり、かといって出る杭を打つ社会に生まれた天才は不幸です。
この事実は今も昔も変わりませんが、今が昔と違うところは、分配ルールによって平等が調整できる姿を、誰もがパソコン1つで試せるようになったことです。
不平等とは、地震や台風のようにコントロール不能な災害ではなく、人がコントロールできる問題です。
もし効率を求める組織だったなら、結果としての不平等より、チャンスとしての公平を敷くべきかもしれません。
あるいは調和を求める社会だったなら、結果としての平等を重んじ、方法としての不公平を受け入れるべきかもしれません。
ひょっとすると、全体最適化のためには適切なセグメンテーション、クラス分けや階級化が必要なのかもしれません。
いずれにせよ、目的に叶ったルールは数字の上で選択可能であり、
たとえそのモデル化が不完全だったとしても、感情にまかせた言葉をぶつけ合うよりずっと合理的だと思うのです。
* なぜ統計学では釣り鐘型の分布が使われ、物理現象では右肩下がりの分布が使われるのか
>> [id:rikunora:20170321]
# 交換のルールを変えてみたら、分布はどのように変わるのか import numpy as np import random import scipy.optimize import matplotlib.pyplot as plt class ExchgRule: # 2つの数の合計をランダムに分配する def exchg(self, a, b): rd = np.random.rand() s = a + b p = (s * rd) q = (s * (1.0 - rd)) return ( p, q ) # 小さい方の数と等量(双方が出せるだけの金額)をランダムに分配する def exchg_min(self, a, b): rd = np.random.rand() mn = min( a, b ) mx = max( a, b ) p = 2 * mn * rd q = 2 * mn * (1-rd) return ( p, q + mx - mn ) # 2つの数のn乗の和が一定になるように分配する def exchg_pwn(self, a, b, n): rd = np.random.rand() s = np.power(a, n) + np.power(b, n) p = np.power(s * rd, 1/n ) q = np.power(s * (1.0 - rd), 1/n ) ratio = (a+b) / (p+q) # 合計が一定となるように標準化 return( ratio * p, ratio * q ) def run(self): N_SAMPLE = 1000 # 粒子数 N_EXCHG = 100000 # 交換回数 # フィットさせたい関数、指数分布 def exfunc(x, a, b): return a * np.exp( - x * b ) # TypeError: only size-1 arrays can be converted to Python scalars # mathパッケージのlogやexpを用いるとエラーが出ます。 # numpyパッケージのlogやexpを用いればオッケーです。 # フィットさせたい関数、正規分布 def nmfunc(x, a, b, c): return a * np.exp( - (x-c)**2 * b ) # フィットさせたい関数、ガンマ分布っぽいもの def gmfunc(x, a, b, c): return a * np.power(x, b) * np.exp( - x * c ) # いろんな分布からスタートしてみる sample = np.random.rand(N_SAMPLE) # 一様分布 # sample = np.random.randn(N_SAMPLE) # 標準正規分布 # sample = np.random.normal( 10, 2, N_SAMPLE ) # 正規分布、平均をずらした # sample = np.random.exponential( scale=1.0, size=N_SAMPLE ) # 指数分布 sample = np.abs( sample ) # 絶対値に直す for i in range(N_EXCHG): a, b = random.sample( range(N_SAMPLE), 2 ) # ランダムに2つの数を選ぶ # p, q = self.exchg( sample[a], sample[b] ) # p, q = self.exchg_min( sample[a], sample[b] ) # 双方が出せるだけを分配 p, q = self.exchg_pwn( sample[a], sample[b], 2 ) # n乗だったらどうなる sample[a] = p sample[b] = q ret = plt.hist( sample, bins=50 ) # ヒストグラムを描く # 曲線あてはめを試みる fit_func = exfunc # exfunc # gmfunc # 関数名が直接代入できるって便利. hist_x = ret[1][:-1] # ヒストグラムの結果は返り値に入っている hist_y = ret[0] param, cov = scipy.optimize.curve_fit( fit_func, hist_x, hist_y ) print( param ) fit_y = fit_func( hist_x, *param ) plt.plot( hist_x, fit_y, '-', color="red") # 曲線を描く plt.show() print( "ave={:.05f}, std={:.05f}, {:.05f}〜{:.05f}".format( \ np.mean(sample), np.std(sample), np.min(sample), np.max(sample)) ) if __name__ == '__main__': me = ExchgRule() me.run()
総合順位が個々の最高順位よりも上となる確率
たとえばトライアスロン3種目で、総合順位が個々の種目のどの順位よりも上になることがある。
これはちょっと意外に思えるので、問題をうんと単純化して2種目で考えてみよう。
赤、青、黄の3人の、数学と英語のテスト結果が上の図のようだったとすると、
青は数学でも2位、英語でも2位でありながら総合順位は1位だ。
なので、(総合順位) > (個々の種目の最高順位) はあり得ることなのだ。
しかし下の図のような状況だと、青が総合1位となるには、英語、数学のどちらかで1位を取らないといけない。
なので、総合順位が上になるかどうかは、周囲の状況で変わってくる問題だったのだ。
さて、トライアスロン3種目の場合は、2種目で線で描いた状況を、立体化して面で描けば良いわけだ。
赤と黄に足を引っ張る不得意種目があったなら、平均的な青が総合1位なることだってあり得る。
では、総合順位が個々の最高順位よりも上となる人は、全体のうちどれくらい居るのだろうか。
ちょっと考えても分からなかったので、パソコンでシミュレーションを行った結果がこれ。
2科目の場合、全体の 1/3 が、
3種目の場合、全体の 1/4 が、
N種類の場合、全体の 1/(N+1) が、
個別の順位よりも総合順位の方が上という、シンプルな結果となった。
この結果からすると、
・種目数が少なければ、突出せずとも満遍なくこなす人が上位に行くことがある。
・種目数が多くなるにつれて、どの分野でも負けないだけでは不十分で、突出した得意分野が望まれる。
以上、シミュレーションの結果は間違い無いだろうと思っているが、
ではなぜ全体の 1/(N+1) となるのか、きちんとした証明ができていない。
2科目、3種目の図を見ると、なんとなく分かるような気もするのだが、うまく説明できない。
誰か賢い人、考えてみて。
# -*- coding: utf-8 -*- """ 総合力ってどのくらいあるの? たとえばトライアスロン3種目で、総合順位が個々の種目の最高順位よりも上となる確率は? """ import numpy as np from statistics import mean class GeneOrder: N_MEMBER = 5000 # 参加人数 # 競技の数を2〜15まで変えて試してみる def run(self): for n_subj in range( 2, 16 ): # 競技の数を変えてみる results = [] for repeat in range( 10 ): # 10回繰り返して平均をとる ret = self.each_run( n_subj ) results.append( ret ) # print( results ) val = mean(results) pred = 1/(n_subj+1) # 結果はおそらく1/(競技数+1) になると予想 # 競技数, 実験値, 予想値, 食い違い print( "{}, {:.5f}, {:.5f}, {:.05f}".format( n_subj, val, pred, val-pred ) ) # 個々の試行 # n_sub: 競技の数 def each_run(self, n_subj): points = [] # 各種目ごとの得点配列 orders = [] # 各種目ごとの順位配列 # 各種目について得点を付ける for i in range( n_subj ): # いろんな分布で試してみよう x_arr = np.random.rand( self.N_MEMBER ) # N個の一様乱数 # x_arr = np.random.normal( 0, 1, self.N_MEMBER ) # N個の正規分布 (平均, 分散, 出力数) # x_arr = np.random.beta( 4, 2, self.N_MEMBER ) # β分布、非対称でやってみよう # 順位についての話なので、分布形状は関係ないようだ。 points.append(x_arr) # 各種目について順位を付ける for i in range( n_subj ): x_arr = points[i] n_order = x_arr.argsort() # 得点に対する順位を得る orders.append( n_order ) # 総合得点を付ける total_points = np.zeros( self.N_MEMBER ) for m in range( self.N_MEMBER ): sum = 0 for i in range( n_subj ): sum += points[i][m] total_points[m] = sum # 総合順位を付ける n_arr = np.array(total_points) total_order = n_arr.argsort() # Min(個別順位)を得る total_min = np.zeros( self.N_MEMBER ) for m in range( self.N_MEMBER ): min_order = self.N_MEMBER + 1 # 最小の順位を得る for i in range( n_subj ): if orders[i][m] < min_order: min_order = orders[i][m] total_min[m] = min_order # 出力してみよう """ for m in range( self.N_MEMBER ): row = [] for i in range( n_subj ): row.append( points[i][m] ) for i in range( n_subj ): row.append( orders[i][m] ) row.append( total_points[m] ) row.append( total_order[m] ) row.append( total_min[m] ) print( ",".join( map(str, row) ) ) """ # 総合順位 < Min(個別順位)をカウント cnt = 0 for m in range( self.N_MEMBER ): if total_order[m] < total_min[m]: cnt += 1 # 結果を返す ratio = cnt/self.N_MEMBER # print( "{}, {}, {}".format( n_subj, cnt, ratio ) ) return ratio if __name__ == '__main__': me = GeneOrder() me.run()
パズルを解く制約プログラミング
このような10枚の板を、四角に組み合わせるというパズル。
行き当たりばったりでは、簡単には解けない。
パソコンに解かせようと探したところ、こんなプログラムを見つけた。
* Coprisによる制約プログラミング入門
>> http://bach.istc.kobe-u.ac.jp/copris/docs/intro-ja.html
“制約プログラミング”とは、制約条件をコンピュータに入れると、コンピュータが条件に合った答をはじき出す、というもの。
Coprisの場合、条件を整数の数式の形で入力すると、答にあてはまるパターンが次々と出てくる。
この感覚を口で説明するのは、なかなか難しい。
たとえば上のパズルを解くプログラムは、こんな感じになる。
* まず答が入る容れ物となる、5x5の変数を用意する。
この全部で25個の変数は、それぞれ -1, 0, +1 の値のいずれかを取るものとする。
+1 は長い切れ込み、-1 は短い切れ込み、0 は普通の長さの切れ込みを表すことにする。
* 10枚の板には +1 と -1 が1個ずつ入っている。
[条件1] 5x5の変数の、それぞれ縦の列の合計 = 0 となる。
[条件2] 5x5の変数の、それぞれ横の行の合計 = 0 となる。
[条件3] 5x5の変数の、それぞれ縦の列の絶対値の合計 = 2 となる(+1 と -1 の2個が入っている)。
[条件4] 5x5の変数の、それぞれ横の行の絶対値の合計 = 2 となる(+1 と -1 の2個が入っている)。
* 10枚の板のパターンが全部異なっている。
板を裏返しに差し込むこともできるが、それらのパターンも全て異なる。
[条件5] 5カ所の切れ込みを2進数と見なしたとき、2進数の値が縦横全部で異なる。
2進数は、切れ込みを右から左へ読んだパターンと、左から右に読んだパターンの全てが異なる。
* Scalaソースコードはこちら・・・
>> http://brownian.motion.ne.jp/memo/Copris/CrossBoard.scala
>> http://brownian.motion.ne.jp/memo/Copris/CrossBoardMain.scala
このような制約条件をセットして、答を探せ(find)と命令すると、Coprisが次々と答を出してくる。
試したところ、176パターンの答が出てきた。
このパターンの中には上下左右前後をひっくり返しただけの答も含まれているので、実質的には 176÷8=22 パターンの答があるようだ。
1パターンだけ示すと、こんな風になる。
0 -1 0 0 1
-1 1 0 0 0
0 0 1 -1 0
1 0 0 0 -1
0 0 -1 1 0
* 全ての解はこちら・・・
>> http://brownian.motion.ne.jp/memo/Copris/CrossBoardSol.txt
■ 班分け問題
パズルを解くプログラムなんて、ピンポイントでマニアックなものかと思いきや、これが案外役に立つ。
実際、私の役に立ったのは“相性のあるグループ分け問題”だった。
40名ほどのメンバーを、5〜6名×7グループに班分けしたかったのだが、
メンバー同士には相性があって、この人と組みたい、この人とは一緒になりたくない、といった希望がある。
これが40人分ともなると、いちいち希望を聞いて班分けするのは実に面倒くさい。
場合によっては、あっちの希望はかなったのに、なぜこっちの希望はかななわないのか、など、不平不満になりかねない。
そこで制約プログラミングの出番である。
* まず答が入る容れ物となる、(メンバー数)x(グループ数)の変数を用意する。
これらの変数は、それぞれ 1, 0 のいずれかの値を取るものとする。
1 は、そのメンバーがそのグループに属していることを意味する。
* [条件1] 各メンバーは、どこかのグループに属する。
変数の、メンバー行の合計 = 1。
* [条件2] 各グループに属する人数は決まっている。
変数の、グループ列の合計 = (所定の人数)。
* [条件3] 仲良し同士は同じグループ。
仲良し同士について、変数をグループ列方向に掛け算した合計 = 1(どこかのグループで1×1となる)。
* [条件4] 嫌い同士は異なるグループ。
嫌い同士について、変数をグループ列方向に掛け算した合計 = 0(すべてのグループで1×1とはならない)。
* Scalaソースコードはこちら・・・
>> http://brownian.motion.ne.jp/memo/Copris/Groups.scala
好き、嫌いの条件をたくさん入れすぎると、解無しになってしまう。
そうなったとき、1つずつ条件を減らしてゆくと、どこかで解が出てくる。
つまり、誰が我慢すれば丸く収まるのか試すことができる。
■ 環境設定
制約プログラミングのソフトウェアはいくつかあるが、Coprisの良いところは敷居が低いことだと思う。
とにかくScalaさえ動かせれば、Copris自体で覚えるべきことはかなり少ない。
なので、「制約プログラミングとは何ぞや」を知るにはベストなのではないかと思う。
ただ、この「Scalaさえ動かせれば」のところでつまずく人も多いと思うので、Windows上での簡単な導入方法を以下にメモっておく。
(実際「Scala インストール」で検索すると、やれ開発ツールを入れろ、sbtを入れろ、
といった方法がヒットするので、目的に到達する前に息切れしてしまう。スタートはもっと簡単でよい。)
(1). Java runtime version 1.8 以降をインストールする >> http://www.java.com
(もちろんJDKでもかまわない。試しにコマンドプロンプト上で、
> java -version
と入力してみて、version 8 以上と出てきたらインストールは不要。)
(2). Scala version 2.11 をインストールする
* Scala Download >> https://www.scala-lang.org/download/
『CoprisはScala version 2.11で動作する (他のバージョンでは動作しない).』
とあるので、現在の最新版ではなく、前のバージョンを入手する。
Scalaダウンロードページの下の方に「Other Releases」「Scala 2.11.12」とあるので、そちらをクリック。
SCALA 2.11.12ダウンロードページには「DOWNLOAD INTELLIJ」「DOWNLOAD SBT」とあるのだが、
それぞれ本格的開発向けなので、そこはパスする。
ページ下の方にある「Other resources」「scala-2.11.12.zip」から、直接zipファイルをダウンロード入手する。
(3). Javaと Scalaにパスを通す。coprisにクラスパスを通す。
作業するコマンドプロンプト上で、以下のように入力するか、以下のようなバッチファイルを作っておく。
("C:\MyWork"といった箇所は、各人の環境に応じて適切な場所をセットする。)
SET JAVA_HOME=C:\MyWork\java\10
SET SCALA_HOME=C:\MyWork\Scala\scala-2.11.12
PATH=%PATH%;%JAVA_HOME%\bin;%SCALA_HOME%\bin
SET CLASSPATH=.
SET CLASSPATH=%CLASSPATH%;C:\MyWork\Scala\copris-v2-2-8\build\copris-all-v2-2-8.jar
この状況で > scala と入力すると、scala対話プロンプト(REPL)が立ち上がる。
C:\MyWork\Scala>scala
Welcome to Scala 2.11.12 (Java HotSpot(TM) 64-Bit Server VM, Java 10).
Type in expressions for evaluation. Or try :help.
scala>
(4). 以降の操作は、Copris入門ページにある通り。
* Coprisによる制約プログラミング入門
>> http://bach.istc.kobe-u.ac.jp/copris/docs/intro-ja.html
チェビシェフの不等式のかんたん理解
どのような標本・確率分布でも・・・平均から 2標準偏差以上離れた値は全体の 1/4 を超えることはなく、
一般にn標準偏差以上離れた値は全体のを超えることはない。
>> wikipedia:チェビシェフの不等式 より.
式で表すと、
P() は、カッコの中が成り立つ確率、という意味。
μは平均。|x-μ| は、個々のデータの値と平均との偏差のこと。
σ は標準偏差。
a には任意の数を当てはめることができる。
* そんなの常識、あたりまえでない大数の法則 >> http://miku.motion.ne.jp/stories/08_LargeNum.html
このように書くと何だかとても難しいことのように思えますが、実はアタリマエのことを言っているに過ぎません。
● 最も単純な標準偏差1の分布
最も単純な標準偏差1の分布は、データが +1と -1の、2個だけというものでしょう。
標準偏差σ = √{ (1^2+ (-1)^2) / 2 } = 1。
この状況をチェビシェフの不等式にあてはめると、
『平均0から、1標準偏差以上離れた値は全体の 1/1 を越えることは無い』
つまり、全部のデータを1よりも遠くに引き離すことはできない、ということを言っています。
試しにデータを少しだけ動かして +1.1 と -1.1 にしたならば、それに合わせて標準偏差も 1.1 と大きくなります。
ならば、+1.1 と -0.9 といった具合に動かしてみると、今度は平均が 0.1に上がるだけで、
やはりどちらのデータも標準偏差の1.1を上回る(あるいは-0.9を下回る)ことはありません。
つまり『標準偏差とは、データを2個の点で代表させたとき、その広がり方のこと』だったのです。
平均値を『データを1個の点で代表させたとき、その値のこと』だと考えれば、
標準偏差とは、いわば“平均値の2個版”だと見なせます。
データが2個だったとき、チェビシェフの不等式が主張する通り「どのデータも標準偏差を超えることはない」、
・・・そもそも2個のデータの隔たりのことを標準偏差と呼んでいたのだ、と理解できます。
● 標準偏差が2を越える分布
次に、一部のデータが標準偏差2を越えるような、なるべく単純な分布を考えてみましょう。
2個のデータを +2と -2 に置いて、これらがちょうど標準偏差2に位置するように調整すると、こうなります。
データを +2 と -2 に1個ずつ、あとは0を6個配置する。
最も隔たりの大きい +2, -2 のデータをちょうど標準偏差2の位置に持ってくるには、
標本全体としての標準偏差を1に調整しなければなりません。
それには、±2の広がりを打ち消すだけのデータを平均の0に置く必要があります。
(必ずしも0に置かなくても良いのですが、0に置くのが標準偏差を縮めるには最も効率的です。)
標準偏差を1に保つには、
{ (+2)^2 + (-2)^2 } / (全データの個数) = 1
となるので、(全データの個数) = 8 だと分かります。
このとき、標準偏差2を越える(2以上の)データは8個中2個なので、
確かにチェビシェフの不等式が主張する通り 1/2^2 = 1/4 となっています。
● 標準偏差がNを越える分布
同じことを、標準偏差3を越える場合で考えると、こうなります。
データを +3 と -3 に1個ずつ、あとは0に16個配置する。
(全データの個数) = 3^2 × 2
・なぜ2乗するかというと、そもそも分散とは各データの偏差の2乗の合計だったからです。
・なぜ2倍するかというと、プラス側とマイナス側で2倍になるからです。
標準偏差4を越える場合は、こうなります。
データを +4 と -4 に1個ずつ、あとは0に30個配置する。
(全データの個数) = 4^2 × 2
『標準偏差Nを越えるデータを1個置きたかったなら、N^2 個より多くのデータを0に置く必要がある』
これが、チェビシェフの不等式の意味するところだったのです。
東京→青森、国道4号を通らない山岳ロングライド
東京->青森 732.43km、国道4号を一切通らない山岳ルートを自転車走破!
2018年 9月 23日 AM3:00:00 〜 翌 9月 24日 15:13:43.
時間: 36時間13分43秒 (途中 2時間程度の仮眠)
平均時速: 20.2km
コース: 東京日本橋->江戸川CR->日光->鬼怒川->会津若松->長井->寒河江->新庄->横手->角館->大館->弘前->青森.
■ ルートラボGPS記録
(前半)日本橋〜山形新庄 >> https://yahoo.jp/pji0Nv
(後半)山形新庄〜青森 >> https://yahoo.jp/JX4z0m
■ ことの起こり
今年のシルバーウィークも、どこか遠くに行こうと計画を練っていた。
当初、まだ果たしていない大阪→東京キャノンボールに挑もうと考えていたのだが、
周囲の猛反対に合ってあえなく取り下げとなった。
そこで計画を改めて、できるだけ交通量が少ないルートで遠くまで行くことにした。
(実は同じことを3年前にもやった気がする。。。今後、大阪→東京を走ることはもう無いだろう。)
まっさきに候補に挙がったのは、今年のGWに行った秋田までの再チャレンジだ。
・2018/4/28 東京→秋田ロングライド >> d:id:rikunora:20180604
あの時は予想を超える寒さに苦しめられたが、今度は十分な防寒装備で挑んでみようか。
改めて Google Mapを眺めると、秋田までの道をそのまま延長すれば、青森まで達することに気が付いた。
距離を測ってみると、4号線経由と大差無い。
東北の真ん中を突っ切って行くのだから、むしろ距離的には少し短い。
もちろんアップダウンはあるのだが、それでも1000mを越える峠は無い。行けそうだ!
東京→青森は、3年前に4号線経由で行ったことがある。
・2015/9/19〜20 東京→青森ロングライド >> d:id:rikunora:20151001
あの時は、とにかく飽きるほど長かったという記憶しか無いのだが、
それでも運良く34時間以内に走りきることができた。
今回は1日半=36時間を目標に青森を目指すことにした。
今回も、着替えと輪行袋をあらかじめ青森中央郵便局に局留めで送っておいた。
ただ、輪行袋については別に緊急脱出用の軽量のものを携行した。
今回はスケジュールぎりぎりの、走行後の翌日午後には出社予定だったので、万が一でも帰れるように備えたわけだ。
■ 機材
・Time VX Elite
・パーツ: Dura-Ace 7800, ワイドレシオFront:50x40, Rear:11x28
・ホイール: Ksyrium SLS
もうこれ以上はないだろうと思っている、ロングライドの鉄板機材。
・タイヤ: Continental Grand Prix TT
・チューブ: Panaracer R'Air 軽量チューブ
この Grand Prix TT、名前の通り Time Trial用タイヤで、軽くて速い。
全体的に薄いのだが、それでも今までパンク無しの優れものだ。
さらに今回はパンクのリスクを恐れず軽量チューブにしてみた。
この組み合わせの走り心地はすばらしい。
・フロントライト: CatEye Volt300×2 -- バッテリーはVolt400のもの.
・リアライト: CatEye Rapid-mini×2
・バーエンドライト: CatEye LOOP2 -- トンネルなどで手を離さずに点灯できる.
Volt300 に Volt400 のバッテリーを付けると、点灯時間が長持ちする。
ライトは前後とも、同じものを2個ずつ装備した。
たとえ1個がトラブったとしても、もう片方で乗り切るためだ。
あと、サイコンは持って行かなかった。(記録はGPS-Watchでとった。)
途中で電池切れになることが分かっていたし、これほどの長距離で、
途中のスピード経過をいちいち気にするのが良くないように思えたので。
■ 服装
ついこのあいだまで猛暑だったのにもかかわらず、東北の夜はかなり冷え込むらしい。
そのため服装についてはかなり悩んだ。
天気予報を参考に、昼は28度〜夜は10度まで耐えられる装備を選んだ。

反射ベスト(Biemme)、防寒用の上着(cannondale, 袖が着脱できてベストにもなる)、ろんぐらいだぁす!ジャージ。

蛍光ウィンドブレーカー(CRAFT)、アンダーシャツ(CRAFT)、タイツ(PearlIzumi)、靴下(PearlIzumi)。

手袋は2重、手が痛くなるので。寒さに備えてのメットインナーキャップは功を奏した。
今回よかった一品は、CRAFTの長袖アンダーシャツ。
下着にしてはかなり高いと思えるお値段だったのだが、実に快適。
下着には贅沢する価値があることを覚えた。
日中はこの長袖アンダーシャツの上に、半袖サイクリングジャージ、反射ベストというスタイル。
夜はウィンドブレーカー、あるいは防寒上着を着用した。
■ 緊急Goods
緊急脱出用の軽量輪行袋(SL-100)。野宿のためのレスキューシート。今回は共に出番が無かった。
■ 経過
・深夜3:00、日本橋道路元標を出発。
出発時の持参食料、おにぎり×3個、ウィダーインゼリー×2個。
・国道4号を通らないよう、まずは東へ。
隅田川沿い、スカイツリーの傍らを抜け、国道6号を一路江戸川へ。
金町から江戸川サイクリングコースに入る。
・江戸川CR、深夜はほばがら空きだが、ごく希に散歩、ランニングに出会う。
気がつくとハンドルにたくさんの蜘蛛の巣がくっついている。
・境から県道17号に入る。一瞬、雨がぱらついたが、降られることはなかった。
古河付近の路面は濡れていた。際どいところで雨を回避したようだ。
・県道から細い抜け道ルートで小山へ抜けた。ここでおにぎりを食べる。
・小山郊外「扶桑第一公園」でトイレ休憩、おにぎりを全て食べる。今回、朝からやたらと腹が減る。
・壬生町、鹿沼を抜け、日光までは微妙な登り。
・日光、大谷川を渡る橋のたもとでトイレ休憩、ウィダーインゼリーを消費。
・鬼怒川バイパス、日塩有料道路を通る。それぞれ50円、20円。
・川治温泉トンネル手前で休憩、最後のウィダーインゼリー消費。食料が全て無くなった。
・すばらしい景色の山道、だが何も無い。腹が減ってやばい、ハンガーノックが近い。
・中三依(なかみより)温泉「山の幸直売センター」にたどり着き、
店のおばちゃんに「腹が減って動けない、何か食べ物をください」と訴える。
親切なおばちゃんが、奥からカボチャの煮物と栗ご飯を出してくれた。
空きっ腹に染み渡るようにうまかった。おばちゃん、ありがとう!
しかも無料。申し訳ないので、ジュースにアイス、ビスケット類を購入した。

(写真は Google Mapより)
・薄曇りから晴に代わり、気温上昇。いいかんじに山王トンネルを越える、標高846m(GPS読み)。
・山間の田んぼの中を下り調子で会津若松へ。途中、下郷付近で自販機休憩。
・会津若松では、ちょうど「会津祭り」で賑わっていた。侍のかっこうをした人が練り歩いていた。
駅前は混雑で通れなかったため、裏手に回る。
・13:20「ファミリーマート会津金川町店」で休憩補給。
・国道121で喜多方市街をバイパスし、「道の駅 喜多の郷」でトイレ休憩。
・大峠登り途中、日中ダムで12時間経過。この大峠の道の眺めはけっこう好き、トンネル多いけど。
だいぶ疲労が溜まってきたが、まだ全行程の1/3と思うと笑いがこみ上げてくる。
・トンネルを越え、山形県道4号、次いで県道8号に入り、川西町へ。
ここはGWに訪れたとき工事中で走れなかったところ。
田んぼの中、良い風景の道。このあたりで手持ちのおにぎりを次々と消費。
・米坂線、今泉駅付近の稲荷神社で休憩。
自販機ジュースと最後のおにぎり消費。ここではGWのときにも休憩した。
何気ない場所なのだけれど、ちょうどこの辺りで疲労が溜まるポイントだし、水道もあるし、ここで休みたくなるのだな。
・長井通過、最上川沿いに北上。対面で何台かのロードに出会う。
・荒砥から国道287を最上川沿いの道に入る。ここはGWのときに道を間違えたところだが、今回は大丈夫。
・「道の駅 白鷹ヤナ公園」でトイレ休憩。
あゆ祭りをやっていたようだが、もう終わりの時間だった。
ここからライト点灯、ナイトランに入る。
・朝日町、寒河江、河北、国道347に入って村山市、問題なく通過。
明かりも交通量少ない。この辺りでようやく全行程の半分。
GWには寒くてたまらなかった記憶があるのだが、今回は気温20〜18度で涼しいくらい。
走行感覚がまるで違う。
・大石田駅前から県道を通って国道13号に入る。
・舟形トンネルあたりで、眠気と疲労が襲ってきた。
少し先の南新庄駅(無人駅)ホームの待合室で仮眠をとる。
完全個室、トイレ付き(?!)の快適なところだ。21:00〜30分程度の休憩。

(写真は Google Mapより)
・22:22「ファミリーマート新庄昭和店」で遅めの夕食。
おにぎりが喉を通らなくなってきているので、甘いパン食とする。
(ここで買った予備のおにぎり1個は、結局最後まで食べずに持ち越した。)
・深夜23:30、旧道の主寝坂峠を越える。真っ暗、すれ違うものは何も無い。
・峠を越えてから下り坂、走りやすくなる。
しかしここから明け方にかけて、疲労と睡眠との戦いとなる。
・0:26「道の駅 おがち 小町の郷」で休憩をとる。
いよいよ気温が下がってきたので防寒上着を着用。やはりこれが役に立った。
気温は最も低いところで12度の表示を見た。
これは1回だけで、あとは16〜18度程度だった。
(この街道沿いには気温の表示があるのだ。)
東京の暑さからは想像しにくいところだが、これもGWの経験のおかげ。
・3カ所続く道の駅「おがち 小町の郷」「十文字」「雁の里せんなん 雁太郎」は、
休憩室が24時間開いていると事前に調査済み。(今回せんなんは通過した)
・次の道の駅「十文字」で眠気が極に達した。
休憩所に寝られるような場所は無かったのだが、構わずカーペットの床でごろ寝する。
(GWにやむなく寝た、公園のトイレの中より数倍マシだ。)
1:30〜2:39、約1:00の仮眠。
・横手の手前で深夜3:00、24時間が経過した。仮眠してもやはり眠い。
(この感触からすると、24時間東京->秋田は極めて困難だ。)
・美郷から県道11号に入り、角館を目指す。
この間、眠くて疲れてひたすら長かったという思い出しか無い。
昼間に走れば、さぞ良いところだったろうに・・・
・角館で夜明けを迎える。
5:00〜5:34、角館市街を抜けた付近のバス停「元町」で約30分の仮眠をとる。
雪国のバス停は立派な個室になっているのだ。疲労のあまり熟睡する。

(写真は Google Mapより)
・目が覚めると辺りは薄曇り。
ここから北秋田市まで約100km、途中、想像以上に何も無いことに驚く。
地図を見ると鉄道に沿っているのだが、なぜこんなところを走っているのだろうか。
疑問に思っていたところ、1両だけの汽車がコトトン、コトトン、と追い抜いていった。
なんとも感動を覚えた。(秋田内陸縦貫鉄道、知る人ぞ知るローカル線だ。)
・このあたりが最も精神的につらかった。
上り坂なのでペースが上がらない。
残り200km(東京-静岡以上!)あると思うと、本当に青森にたどり着けるのかと疑いの念が頭をもたげる。
幸い輪行袋も持っていることだし、あの電車に乗ってしまえば良いのではないか・・・
・足を引きずるように前進を続けると、いつしか登坂のためチェーン脱着所の前を通過した。峠が近いようだ。
7:51、やっとのことで大覚野峠を越え、青森まで行く自信を取り戻す。天気も晴れてきた。
・ひたすら山中の長い道を下り、9:40「ローソン 北秋田米内沢諏訪岱店」で補給と休憩。
ようやく町に戻ってきた。
・鷹の巣から国道7号線に入る。青森まであと105kmの看板を見る。もう少しだ。
あと少しという気持ちも手伝って、不思議と新たな力が湧いてきた。
国道7号は交通量が多い。ここまでの山中に比べれば圧倒的。
(というより、ここまでの交通量が異様に少なかった。)
・大館を通過した先で、大荷物のキャンピング自転車に会った。なんでも神奈川から来たのだとか。
・12:09、矢立峠。これまで越してきた峠に比べれば道も良く、問題なく越せた。いよいよ青森県だ。
・12:28「道の駅 碇ヶ関」で最後の大きな休憩。手持ちの黒糖まんじゅうを食べる。
(ここは以前、東京->青森ランでも立ち寄ったところだ。立ち寄った時刻もかなり近い。)
・ここから青森までは2通りの道がある。
(1)国道7号をひたすら走る。(2)県道を通り黒石、青森空港を経る。
(2)は以前走ったルートなのだが、路面があまり良くなく、青森空港への登りもあることから、今回は(1)を選んだ。
・ところが国道7号は、弘前付近からいよいよ交通量が増え、大型トラックもたくさん通るようになった。
1カ所、陸橋の階段を上らなければならないところもあった。
幸い自転車が走れる路肩は広く取ってあったのだが、この路肩はあまり整備されておらず草ぼうぼうで苦労した。
・しかも国道7号にも、青森の手前には山越えがあった。総合的には(2)青森空港ルートの方がよかった。
これも両方走ってみなければ分からないことなのだが。
・9月24日 15:13:43、ようやく青森県庁前に到着。長い長い道のりであった。
感想、『もうこれ以上走りたくない(笑)』
■ おまけ
Google がオートバイと認識!
練習のべき乗則
『練習は裏切らない。』
この言葉の真偽に一石を投じる、驚くべき研究結果があります。
* 第50回 練習の効果 >> http://www.pitecan.com/articles/WiredVision/wv50/index.html
木村氏は、吉澤章氏の「創作折り紙」という本で紹介されている「みそさざい」という作品を15万回折り続け、折るのにかかった時間がどのように変化したかを記録しました。
その結果、折るのに要した時間は、練習回数の対数に比例するという、
「練習のべき乗則」(Power law of Practice) に従うことが明らかになりました。
『意外性に魅せられて約10年続けました』なのだそうです。
* 中京大学 人工知能高等研究所ニュースNo.17
>> http://www.iasai.sist.chukyo-u.ac.jp/pdf/iasai_news17.pdf
15万回、10年という努力は並大抵ではありませんが、数十回程度の繰り返しであれば、日常の中でもよく行うことがあります。
そうした作業を繰り返すと、慣れることによって、どれほど作業時間が短くなるのか。試しに測ってみました。
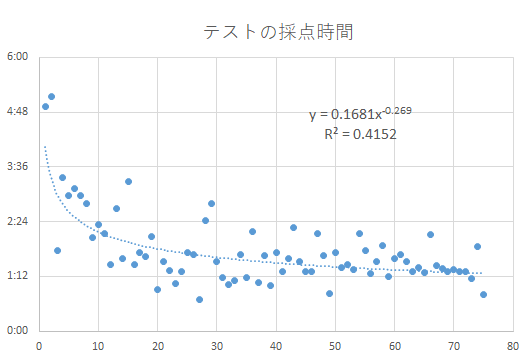
実際に私が試したのは「答案の採点」という作業です。
75枚の答案の採点にかかった時間をストップウォッチで測り、まとめた結果がこのグラフです。
グラフ中に引いた曲線は、(採点の秒数) y = 0.1681 x ^ (-0.269) という累乗曲線。
なるほど、かかった時間はおおむね「練習のべき乗則」に一致しています。
同じ内容ですが、グラフを両対数で描き直したものが下になります。
ここで、直線が「練習のべき乗則」なので、全体の傾向としては合っています。
Wikipediaの「学習曲線」によると >> wikipedia:学習曲線
ピロリとアンダーソンは a 、b の実測値をそれぞれ1.40、0.24と求めた。
この式はかなり普遍的に成り立つ。
この 0.24 という冪乗の定数 b は、私の測定値では 0.269、なので、確かに近い値になりました。
一方、折り紙の方はグラフから見ると 0.172(あるいは 0.2166)となっており、かなり違っているように見えます。
(係数 a は単位の取り方によるように思えるのだが、、、よくわからん。)
また、以下の論文では b = 0.269 、奇しくも私の値と一致していました。
* スキル学習におけるスランプ発生に対する事例分析的アプローチ
>> https://www.jstage.jst.go.jp/article/tjsai/23/3/23_3_86/_pdf
こうして見ると、べき乗則自体は普遍的に成り立ちそうですが、
その定数値まで普遍的というのは疑念の余地があり、やはり作業内容によって変わってくると思うのです。
■ 気付いたこと
* べき乗則は確かに有用.
たった75回程度でも「練習のべき乗則」が見えてくるとは驚きです。
最初にかなり時間がかかったのは、解答が本当に妥当かどうか、文献にあたって調べた時間などが含まれています。
それが後半になると、似たような解答は覚える、途中の過程まで覚えて一目で点数が分かる、などの効果が実感できました。
練習のべき乗則は、ちょっとした繰り返し作業にも十分有効なのです。
* 時間がかかるのは記述の読み取り.
テストの採点で最も悩むのは、記述式の解答を読み取って、意図を解釈することです。
テスト問題のように限定された状況下でさえ、答は予想以上にバラエティに富んでいます。
「なるほど、そう来たか」と唸るような解答も少なくありません。
こうした解答の意図を汲み取り、解答者がどのように考えたのか推測を巡らせるところが採点の奥深さなのです。
さらに、当たらずとも遠からずといった解答に、どれだけ部分点を配点するかが悩みどころです。
全体として不公平にならないように、こっちに点数を付けたなら、あっちにも点数が付かないとおかしいぞ、
といった調整を図ることになります。これが難しい。
採点時間の上下動は主に、こうした解答の解釈・調整に充てられています。
この点が、折り紙のように均質な作業と、採点のように1つ1つが異なる作業との違いで、採点時間が大きくばらつく理由です。
それでも実際に測ってみると、解釈に悩む時間はせいぜい数十秒程度であることも分かりました。
* 満点と0点は採点が早いか.
良くできた模範答案と、その反対に白紙に近い答案は、採点時間があまりかかりません。
評価に悩むことが無いからです。
正直、みんなが100点取ってくれれば、採点する側はとても楽です。
評価に悩むのは上位層でも下位層でもない、最も数の多い中間層です。
このことは体感的には明らかなのですが、それが採点時間に表れているでしょうか。
そこで、テストの点数と採点時間の関係をプロットしたのが、このグラフです。
中央付近が膨らんでいるように見えなくもないのですが、今ひとつはっきりしません。
それでも「90点以上は採点に2分かかっていない」というのは事実です。
さらに採点への慣れの影響を除くため、(テストの点数)×(べき乗則からの残差)をプロットしてみました。
グラフからはっきりした傾向は読み取れません。
中間層では「大きく時間がかかる場合もある一方、さっさと済んでしまうものもあり、振れ幅が大きい」
というのが事実のようです。
いずれにせよ、もしべき乗則が普遍的なら、最初の伸び方を見て、その後、どの程度練習すればどこまで伸びるかの予測が立つはずです。
この予測をもとに、どこまで練習すべきか、あるいはどこで練習を打ち切るべきかの判断が付くわけで、これは極めて有用なルールと言えるでしょう。
「みそさざい」の折り紙。折ってみました。
指数法則を満たす非連続関数
『さらっと言うと、要は、選択公理を認めると f(mn)=f(m)+f(n) を満たす不連続関数が作れてしまう。』
以下にあった、気になる数学ネタ。
* PRMLガール 〜 文芸部のマネージャーが「パターン認識と機械学習」を読んだら
>> http://d.hatena.ne.jp/n_shuyo/20130117/prml
このブログ記事には書籍版があって、「あとがきがわりのACガール」にもう少し詳しい解説があります。

PRMLガール―文芸部のマネージャーが「パターン認識と機械学習」を
- 作者: 中谷秀洋
- 出版社/メーカー: 暗黒通信団
- 発売日: 2013/09
- メディア: 単行本
- この商品を含むブログ (4件) を見る
当初は「何のこっちゃ?」と思っていたのですが、最近ようやく意味が分かってきたので、以下につらつらと書いてみます。
(PRMLガールでは対数について書かれていましたが、ここでは指数について書きます。)
関数 f が、全ての実数 x, y について、
f(m + n) = f(m)・f(n)
という関係を満たすとき「f は指数法則を満たす」ということにしましょう。
指数法則を満たす連続関数は、いわゆる指数関数 f(x) = a^x しかありません。
なぜかというと、
【Step.1】 自然数 n については・・・
f(n) = f(n-1)・f(1) = f(n-2)・f(1)・f(1) = ・・・ = {f(1)}^n
ここで a := f(1) と置けば、f(n) = a^n となる。
【Step.2】 0については・・・
f(0) = f(0 + 0) = f(0)・f(0) = f(0)・f(0)・f(0)
よって、f(0) = 1
【Step.3】 マイナスの数については・・・
1 = f(0) = f(n - n) = f(n)・f(-n)
よって、f(-n) = 1 / f(n)
【Step.5】 分数については・・・
f(1) = f( 1/n + 1/n + 1/n ・・・ ) = {f(1/n)}^n
よって、f(1/n) = n√f(1) = n√a
※ n が偶数の場合、f(1/n) = ± n√a という正負の2つが考えられるが、
※ f が自然に連続となるようなプラスの方を採用することにする。
【Step.6】
あとは有理数の極限をとって、連続となるように実数全体に拡大する。
なので、滑らかな連続関数に限れば f(x) = a^x となるのですが、
ここで連続関数という制限を取っ払って、病的な非連続関数もありにすれば、
指数法則を満たす関数はもっと他にもあるのではないでしょうか。
そう思って上を見直すと、最後の【Step6】を見直せば別の関数が構成できそうです。
病的な関数を探す(でっち上げる)作戦として、実数全体を、
・集合A:有理数と、
・集合B:集合Aに含まれない無理数
の2つに分けることを考えます。
そして、
・集合Aに含まれる数 x については f(x) = a exp(x)
・集合Bに含まれる数 y については f(y) = b exp(y)
のように、A,Bそれぞれに異なる大きさの指数関数をあてがえば、思惑通りの関数が作れそうです。
しかしながら、話はそう単純ではありません。
集合Bに属する無理数の中で、(無理数) + (無理数) = (有理数) となるような数があるからです。
例えば (1-√2)という数も、(1+√2)という数も無理数ですが、
2つを足した (1-√2) + (1+√2) = 2 は有理数となります。
そうなると、集合Bに含まれる数の足し算の結果が集合Aにはみ出してしまい、AとBがきっちり分かれません。
何とかして、集合Bに含まれる無理数同士の足し算を、集合Bの中に閉じ込めておくことはできないか。
そこで登場するのが「同値類」というアイデアです。
実数全体を、足し算の結果がお互いにはみ出さないような、たくさんの(無数の)集合に分けることを考えてみましょう。
実数全体を「有理数×無理数」の巨大な(無限の)表に並べることを考えます。
まず、実数Rに含まれる全ての無理数を横一列に並べます。(数直線を引いて、有理数の点だけを削除します。)
とある1つの無理数 x を選び、もし x の有理数倍 a x が他の無理数 y と一致したら、その一致した先の無理数 y を削除します。
たとえば無理数πを選び出したとき、その有理数倍 2π, 3π, 1/5π, -6/7π・・・ などなどを、ことごとく消せ、ということです。
πという子が1人いれば、他は全て「いらない子」です。
この作業をとことん繰り返せば、ついにはどの無理数を有理数倍しても、他の無理数と重ならない状況ができるはずです。
本当に「いる子」だけが残った状況です。
削除の結果、全ての無理数が消えてしまうことはありません。
たとえば π と √2 の有理数倍が重なることは無いので、少なくともこの2つは残るでしょう。
(残った無理数)×(有理数) の巨大な掛け算の表を作れば、その作り方からして、
掛け算の表には(0を除く)全ての実数が、落ちや重なり無く掲載されているはずです。
「掛け算九九」ならぬ、「掛け算有理・無理」というわけです。
※ 同じ考え方で、代数的無理数と超越数を掛け合わせた「掛け算代数無理・超越」の表もできると思います。
ここまでサラリと書きましたが、この巨大な掛け算表が本当に作れるかどうかは自明ではありません。
というのも、どの無理数を「いる子」と認め、どれを「いらない子」とするか、決め手が無いからです。
決め手が無い、というのは、いったいどこから手を付けてよいのか、順序立てて処理する手順(アルゴリズム)が無い、ということです。
1つ1つの実数を1列に順序立てて整列することができない、と言い換えても良いでしょう。
たとえば、最大の無理数を「いる子」にしようとしても、最大の無理数というものはありません。
最小の無理数も存在しませんし、最も1に近い無理数もありません。
確かに、πという1個の無理数を取り出してしまえば、π×1だけが「いる子」で、残りは「いらない子」にすることはできます。
(有理数を順序立てて処理する手順は存在する。)
しかし、実数の中から全ての無理数を順序立てて取り出す方法が存在しないのです。
『どれも空でないような集合を元とする集合(すなわち、集合の集合)があったときに、それぞれの集合から一つずつ元を選び出して新しい集合を作ることができる』
これを「選択公理」と言います。>> wikipedia:選択公理
上の「有理数×無理数の巨大な掛け算表」は、選択公理を前提として、初めてできることだったのです。
※ 参考: バナッハ・タルスキーのパラドックス >> [id:rikunora:20091021]
※ あと、実数を一列に並べることができるとする「整列可能定理」は選択公理と同値な主張です。(8/16追記)
※ >> wikipedia:選択公理には、選択公理と等価な命題として、整列可能定理、ツォルンの補題、テューキーの補題、などが上げられています。
巨大な掛け算表の、縦一列の並びを「同値類」と言います。
たとえば πの同値類は、2π, 3π, (1/5)π, -(6/7)π・・・ などなど、(有理数)×π という形の数の集まりです。
√2 の同値類は、2√2, 3√2, (1/5)√2, -(6/7)√2・・・ などなど、(有理数)×√2 という形の数の集まりです。
有理数それ自身は、(有理数)×1 という形の同値類に集めることにしましょう。
(この1の列だけは、例外的に1という有理数を持ってきます。1のことを単位元と言います。)
それぞれの同値類には“有理数個”の(加算無限の)要素が含まれています。
そしてこの同値類は、無数に(非加算無限)あります。
・実数 x, y の同値関係を、任意の有理数 a によって x 〜 a y と定義する。
・この同値関係によって、0 を除いた実数 R\{0} を同値類に類別できる。
・(R\{0},・) という乗法群を、有理数の乗法 (Q\{0},・) という部分群で割った剰余群 R/Q が構成できる。
類別を終えた後、とある1つの同値類の中での足し算を考えてみましょう。
たとえば πの同値類の中での足し算、2π+3π=5π, 1/5π+(-(6/7)π)= -23/35π などの答は、
全て同じπの同値類に含まれています。
それというのも、有理数の足し算は有理数の中で閉じているため、
(有理数)×π という形の数同士の足し算の答は (有理数+有理数)×π になるからです。
a π + b π = (a + b) π
どの同値類であっても、同値類の中での足し算は、その同値類の中だけで完結し、他の同値類にはみ出すことはありません。
次に、異なる2つの同値類の間での足し算を考えてみます。
同値類の中には、代表要素(いる子)が π や √2 などといった単純に見えるものと、
(2π+3√2) や (5/6π - 7/8√2) などといった複合的に見えるものがあります。
※ (2π+3√2) は (有理数)×πでも、(有理数)×√2 でも無いので、
※ πの同値類でもなく、√2の同値類でもない、また別の同値類に入っているのです。
そこで、同値類の代表要素について、次の概念を導入しましょう。
・代表要素 z が、他の代表要素 x1, x2, x3・・・ と、適切な有理数 a1, a2, a3・・・ を用いて
z = a1 x1 + a2 x2 + a3 x3 + ・・・
となるとき、z は一次従属であると言う。(複合的に見える)・代表要素 z が、他の代表要素 x1, x2, x3・・・ と、どんな有理数 a1, a2, a3・・・ を用いても
z = a1 x1 + a2 x2 + a3 x3 + ・・・
とはならないとき、z は一次独立であると言う。(単純に見える)
この、一次従属、一次独立という概念によって、同値類の代表要素は2種類に分けることができるはずです。
具体的にどんな操作を行って分類するかは分かりません。非加算無限あるので、想像すらつきません。
でも、分けるための基準ははっきりしているのですから、
とにかく全ての代表要素が一次従属と一次独立に分かれたものとしましょう。
そして、全ての同値類の中から一次従属なものを取り除いて、一次独立なものだけを残しましょう。
こうして残った「縦に有理数×横に一次独立な代表要素」の表を用いて、
(0を除く)全ての実数は、表の中にある数の足し算で一意に表すことができます。
別の言い方をすれば、(0を除く)全ての実数は、表に残った一次独立な代表要素に分解できます。
※ 足し算のやり方が一意であることは、次のようにして分かります。
※ いま、とある数 z が、
※ z = a1 x1 + a2 x2 + a3 x3 + ・・・ と、
※ z = a1' x1 + a2' x2 + a3' x3 + ・・・ のように、
※ 2つの異なるやり方で分解できたとしましょう。(一部の an = 0 であるケースも含めて。)
※ 2つの式の差をとって、
※ (a1 - a1') x1 = (a2' - a2) x2 + (a3' - a3) x3 + ・・・
※ となりますが、これは x1 が一次独立であったという仮定に反します。
一次独立な代表要素のことを「基底」と呼んでいます。
全ての実数は、基底の一次結合((有理数)×(基底)の足し算)として表されます。
幾何学的なイメージを思い浮かべるなら、基底とは、多次元空間の各次元の軸のようなものです。
3次元空間であれば、全ての点は
ax + by + cz
で表されるでしょう。
(x, y, z) はそれぞれ (縦, 横, 高さ) に相当する基底です。
同じように、実数という空間は無限次元
a1 x1 + a2 x2 + a3 x3 + ・・・
で表されることになります。
※ こうした幾何学的イメージを持てば、ここまで(0を除く)と入れてきた注釈がうまく空間の中に収まります。
※ すなわち、空間の原点に0を当てはめればよいのです。
さて、だいぶ目的に近づいてきました。
当初の目的は、指数法則 f(m + n) = f(m)・f(n) を満たす関数作りでした。
実数全体を同値類という無数の集合に分けた後、それぞれの同値類について、適当に異なる定数を加えます。
たとえば f という関数を、以下のように定義します。
・与えられた数 m を、基底 m = a1 x1 + a2 x2 + a3 x3 + ・・・ に分解する。
・各基底ごとに異なる適当な定数 c を定める。
c はわりと何でもよいのだが、たとえば次のようなルールで定める。
基底 xn を10進数表記で表し、最初に出てきた 0以外の数字 c(xn) を取り出す。
たとえば基底がπであれば、π=3.1415…なので、c(π) = 3。
基底が√2だったら、√2=1.414…なので、c(√2) = 1。
・すべての規定について an xn + c(xn) を足し合わせた結果の指数関数を、関数 f として定義する。
基底ごとに異なる適当な定数 c(xn) を足す、というところがミソ。
f(m) = exp( Σ[n]{ an xn + c(xn) } )
例:
m = 1π + 2√2
n = 3π + 4√2
のとき、
f(m + n)
= exp( 1π + 3 + 2√2 + 1 + 3π + 3 + 4√2 + 1 )
= exp( 1π + 2√2 )・exp( 3π + 4√2 )・exp(3)・exp(1)・exp(3)・exp(1)
f(m)・f(n)
= exp( 1π + 3 + 2√2 + 1)・exp(3π + 3 + 4√2 + 1 )
= exp( 1π + 2√2 )・exp(3)・exp(1)・exp( 3π + 4√2 )・exp(3)・exp(1)
確かに、この関数は指数法則を満たしているぞ。
この関数 f をグラフに描けば、exp(n)倍という整数刻みで分裂した、穴だらけの指数関数として表されることでしょう。
あるいは、
・適当な定数 c を、基底と同じ値に定める。
たとえばπという基底に付ける定数はπ。√2という基底に付ける定数は√2。
f( 1π + 2√2 ) = exp( 1π + π + 2√2 + √2 )
といった方法で関数 f を作ったなら、この関数 f のグラフは(y>0の)平面上をびっしりと埋め尽くす、穴だらけの指数関数となるでしょう。
検索したら、こんな記事があった。なるほど。
* ハメル基底とf(x+y)=f(x)+f(y)をみたす関数
>> http://math-note.xyz/set-theory/application-of-hamel-basis/